Quadratic Functions
Prerequisites- Linear Functions
Previously, we discussed linear functions. These functions took on the general form:
$$ y = mx + b $$
where $m$ and $b$ are numbers.
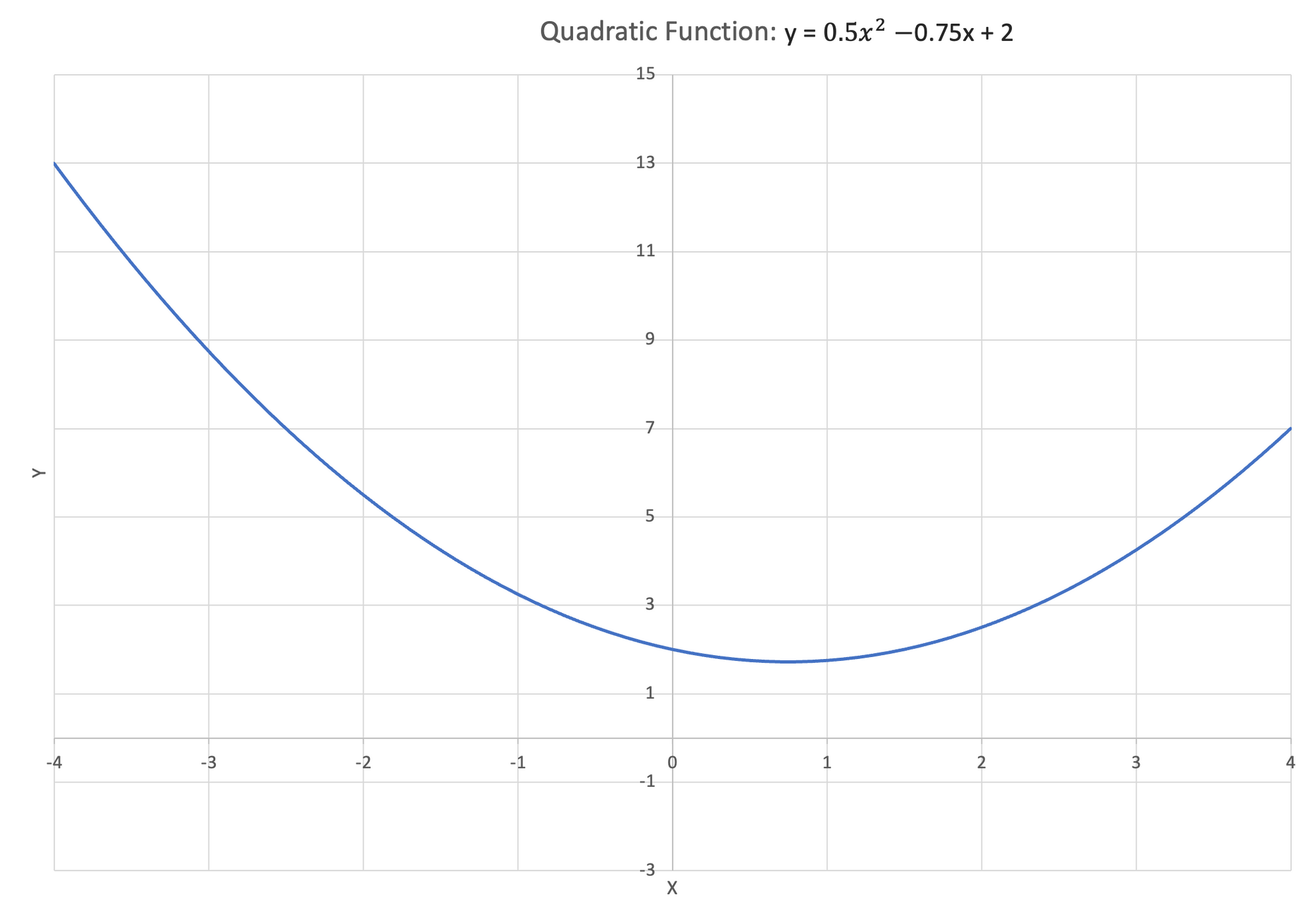
In our math journey, the next kind of functions to learn about are quadratic functions. Quadratic functions include a squared input variable, $x^2$ and take on the general form:
$$ y = ax^2 + bx + c$$
where $a$, $b$, and $c$ are numbers.
Don't confuse the quad in the name quadratic with the prefix corresponding to four. The adjective quadratic actually comes from the Latin word quadrātum, which means square.
When graphed, quadratic functions appear as curves.
Quadratic Function Forms
The most common quadratic function form is the standard form:
$$ y = ax^2 + bx + c$$
where $a, b, c$ are numbers.
Another form for quadratic functions is called the factored form:
$$ y = (dx+e)(fx+g) $$
where $d, e, f, g$ are numbers. The factored form is the easiest for finding roots (to be discussed later).
The last form for quadratics functions we will discuss is called the vertex form:
$$y = g(x+h)^2+k$$
where $g, h, k$ are numbers. The vertex form is the easiest to isolate $x$ using algebraic operations.
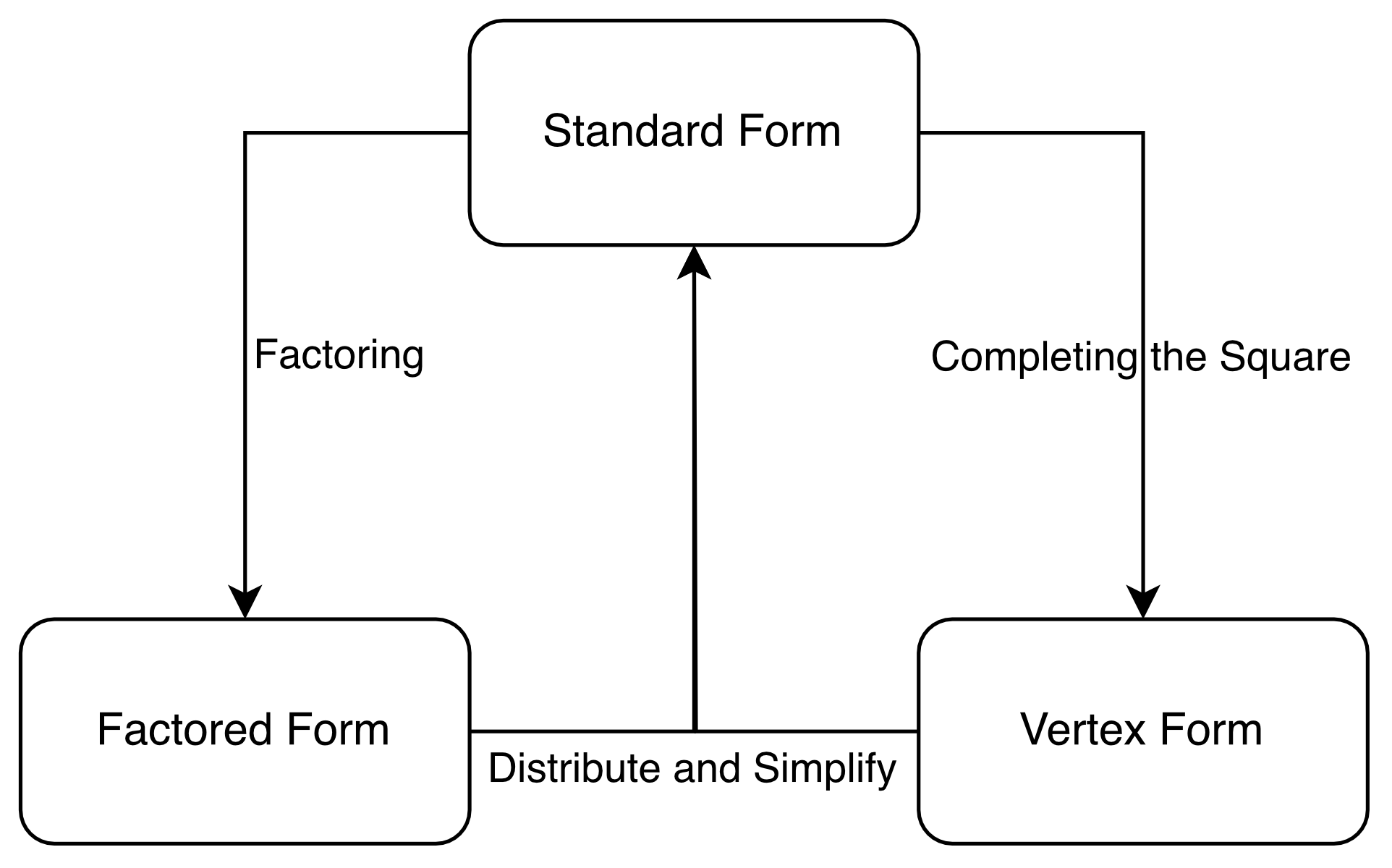
The 3 forms can be changed into each other per the methods shown in the diagram below.
Distribute and Simplify
The factored and vectored forms can be converted to the standard form simply by evaluating and simplifying.
Consider a factored form quadratic equation:
$$ y = (dx+e)(fx+g) $$
We can evaluate the multiplication to obtain the standard form of this equation.
Mathematical Algebra Aid (Distributive Multiplication)
Suppose we have the equation:
$$ 5*3$$
Because $3 = (2+1)$, we can substitute $3$ with $(2+1)$ and obtain an equivalent equation:
$$5*3 = 5*(2+1)$$
Additionally, because $5 = 2+3$, we can substitute $5$ with $(2+3)$ and obtain an equivalent equation:
$$5*(2+1) = (2 + 3)*(2 + 1)$$
Suppose we now wanted to actually obtain the value of this equation. One method would be to undo the steps we just did and evaluate the multiplication:
$$\underbrace{(2+ 3)}_5*\underbrace{(2 + 1)}_3 = 5*3 = 15$$
Another method would be to use the distributive law of multiplication:
$$(2 + 3)*(2 + 1)$$
$$\downarrow$$
$$2*(2+1) + 3*(2+1) $$
$$\downarrow$$
$$(2)*(2) + (2)*(1) + (3)*(2) + (3)*(1)\: [1]$$
Now we can evaluate equation $[1]$ to obtain the final answer:
$$4 + 2 + 6 + 3 = 15$$
Naturally, we are inclined to laugh and mock. Sure, this is a mathematically valid method to calculating the value of the equation, but why would anyone ever want to do this!?
Consider we have another equation and we are asked to simplify it:
$$(x+3)*(x+2)$$
Clearly, the first approach will not work. $(x+1)$ cannot be simplified the way $(2+3)$ can! We are left only with our second method, using distributive multiplication:
$$(x+3)*(x+2) $$
$$\downarrow$$
$$x*(x+2) + 3*(x+2) $$
$$\downarrow$$
$$(x)*(x) + (x)*(2) + (3)*(x) + (3)*(2) $$
$$\downarrow$$
$$x^2 + 5x + 6$$
From this example, the value of distributive multiplication should be more clear. A previously unapproachable problem becomes very manageable.
This technique is often called FOIL, which stands for First Outer Inner Last.
When performing distributive multiplication, multiply the first two terms, the outer two terms, the inner two terms, and the last two terms:
$$(a+b)*(c+d) = a*c + a*d + b*c +b*d$$
$$ y = (d)(f)x^2 + ((d)(g)+(e)(f))x + (e)(g)$$
This of course resembles the standard quadratic form. The formula for converting from factored to standard form is:
$$(dx+e)(fx+g) \longrightarrow ax^2 + bx + c$$
$$ a = (d)(f),\:b = ((d)(g)+(e)(f)),\:c = (e)(g) $$
A vertex form quadratic equation can be converted to standard form by a similar process.
$$y = g(x+h)^2+k$$
$$\downarrow$$
$$y = g(x^2+2hx+h^2)+k$$
$$\downarrow$$
$$y = gx^2+2ghx+gh^2+k$$
$$\downarrow$$
$$y = gx^2+2ghx+(gh^2+k)$$
This of course resembles the standard quadratic form. The formula for converting from vertex to standard form is:
$$ g(x+h)^2+k \longrightarrow ax^2 + bx + c$$
$$ a = g,\:b = gh,\:c = gh^2 + k $$
Completing the Square
The method of completing the square converts a standard form quadratic to vertex form. There is a simple formula to accomplish this:
$$ax^2+bx+c \longrightarrow g(x+h)^2+k$$
$$g = a, \:h = \frac{b}{2a}, \: k = c-\frac{b^2}{4a}$$
Derivation of Completing the Square Formula
For a standard form quadratic function $y = ax^2 + bx + c$ we are seeking to convert it to the vertex form $g(x+h)^2+k$.
If we expand the vertex form equation, we obtain:
$$g(x+h)^2 + k = gx^2+2ghx+(gh^2+k)$$
Setting the standard and vertex forms equal to each other, we get:
$$ax^2 + bx + c = gx^2+2ghx+(gh^2+k)$$
To solve for the conversion formula, we set each $x$ coefficient equal to each other:
$$a = g \:[1]$$
$$b = 2gh \:[2]$$
$$c = gh^2 + k \:[3]$$
To solve for $k$, we start with equation $[3]$:
$$c = gh^2 + k$$
$$\downarrow$$
$$c = \frac{g}{g}gh^2 + k$$
$$\downarrow$$
$$c = \frac{1}{g}g^2h^2 + k$$
$$\downarrow$$
$$c = \frac{1}{g}(gh)^2 + k\:[4]$$
Divide equation $[2]$ by $2$ and substitute into equation $[4]$:
$$c = \frac{1}{g}\left(\frac{b}{2}\right)^2 + k\:[5]$$
Substitute equation $[1]$ into equation $[5]$:
$$c = \frac{1}{a}\left(\frac{b}{2}\right)^2 + k$$
$$\downarrow$$
$$k = c -\frac{b^2}{4a} [6]$$
To solve for $h$, we can again start with equation $[3]$ and substitute $k$ with equation $[6]$:
$$c = gh^2 + k$$
$$\downarrow$$
$$c = gh^2 + \left(c -\frac{b^2}{4a}\right)\:[7]$$
Substitute equation $[1]$ into equation $[7]$:
$$c = ah^2 + \left(c -\frac{b^2}{4a}\right) $$
$$\downarrow$$
$$0 = ah^2 -\frac{b^2}{4a} $$
$$\downarrow$$
$$ah^2 = \frac{b^2}{4a} $$
$$\downarrow$$
$$h^2 = \frac{b^2}{4a^2} $$
$$\downarrow$$
$$h^2 = \left(\frac{b}{2a}\right)^2 $$
$$\downarrow$$
$$h = \frac{b}{2a}\: [8]$$
Consider the quadratic equation:
$$ y = x^2 -2x - 8 $$
Using the formula for completing the square, we obtain that:
$$g = a = 1$$
$$h = \frac{b}{2a} = -1$$
$$k = c-\frac{b^2}{4a} = -9$$
The vertex form of $ y = x^2 -2x - 8 $ is therefore:
$$ y = (x-1)^2 -9 $$
Factoring
The factoring method converts a standard form quadratic equation into a factored form quadratic equation.
Factoring requires knowing the roots of the quadratic equation. A root is just a value of $x$ that causes the equation to be equal to zero:
$$ax^2 + bx + c = 0$$
We will discuss solving for roots in the next section, but for a quadratic equation with roots $m$ and $n$, we can convert a standard from quadratic to a factored quadratic with a formula:
$$ax^2 + bx + c \longrightarrow (dx+e)(fx+g)$$
$$d = 1,\: f = a,\: e = -m,\: g = -an$$
Derivation of Factoring Formula
The goal of factoring is to convert a standard form quadratic into a factored form quadratic
$$ax^2 + bx + c \longrightarrow (dx+e)(fx+g)\:[1]$$
We assume that we know the roots $m$ and $n$.
The standard quadratic form has three parameters, $a$, $b$, and $c$ while the factored form has four parameters, $d$, $e$, $f$, and $g$. This means that there are actually an infinite number of valid factored forms for every standard form. For example, consider the quadratic function:
$$ y = x^2 + 4x + 3 $$
Three possible factored forms of this equation are:
$$ y = (x + 3)(x + 1)$$
$$ y = (2x + 6)(0.5x + 0.5)$$
$$ y = (0.769x + 2.308)(1.3x + 1.3)$$
One means to get a consistent factored form is to always set $d =1$. For example, the below two standard form quadratics converted to factored form follow this guideline:
$$x^2 + 4x + 3 \longrightarrow (x + 3)(x + 1)$$
$$2x^2 + 4x + 2 \longrightarrow (x + 1)(2x + 2)$$
With the assumption $d=1$, we can simplify equation $[1]$:
$$ax^2 + bx + c \longrightarrow (x+e)(fx+g) \: [2]$$
If we expand the generic factored form in $[2]$, we find:
$$ax^2 + bx + c \longrightarrow fx^2 + (g+(e)(f))x + (e)(g) \: [3]$$
For these to be equivalanet, $f$ must be equal to $a$. Let's substitute this into equation $[3]$:
$$ax^2 + bx + c \longrightarrow (x+e)(ax+g) \: [4]$$
Because we know the roots $m$ and $n$, we can substitute them into the generic factored form quadratic in equation $[4]$:
$$(m+e)(am+g) = 0\:[5]$$
$$(n+e)(an+g) = 0\:[6]$$
For equations $[5]$ and $[6]$ to be true, one of two terms from each must be $0$:
$$(m + e) = 0\:[7]$$
$$(an + g) = 0\:[8]$$
We can now solve for $e$ and $g$:
$$e = -m\:[9]$$
$$g = -an\:[10]$$
Consider the quadratic equation:
$$ y = 2x^2 -4x - 16 $$
The roots of this equation are $m = 4$ and $n = -2$.
Using the factored conversion formula:
$$d = 1,\: f = a = 1,\: e = -m = -4,\: g = -an = 4 $$
The factored form quadratic is then:
$$ y = (x-4)(2x+4)$$
Finding Roots of Quadratic Functions
The roots of a quadratic function are the input values that cause the output to be zero.
$$ax^2 + bx + c = 0$$
For example, the roots of $ y = x^2 -2x - 8 $ are $4$ and $-2$.
If a quadratic function is in factored or vertex form, the roots are very easy to determine through direct solving. If a quadratic equation is in standard form, we can use the quadratic formula.
Roots of Factored Form Quadratic Functions
Given a factored quadratic function $y = (dx + e)(fx + g)$, the roots $m$ and $n$ are:
$$n = -\frac{e}{d},\: m = -\frac{g}{f} $$
Derivation of Roots of Factored Form Quadratic Functions
A factored quadratic equation has the form:
$$y = (dx + e)(fx + g)$$
Solving for the roots is as easy as setting each term equal to $0$:
$$0 = \underbrace{(dx + e)}_0 \underbrace{(fx + g)}_0$$
$$dx + e = 0$$
$$\downarrow$$
$$x = -\frac{e}{d}\: [1]$$
$$ fx + g = 0$$
$$\downarrow$$
$$ x = -\frac{g}{f} \: [2]$$
For example, consider the factored form quadratic function:
$$ y = (x-4)(2x+4)$$
The roots are $n = 4$, $m = -\frac{4}{2} = -2$.
Roots of Vertex Form Quadratic Functions
Given a vertex form quadratic function $y = g(x+h)^2+k$, the roots $m$ and $n$ are:
$$m,n = -h \pm\sqrt{\frac{-k}{g}} $$
Derivation of Roots of Vertex Form Quadratic Functions
Set the generic vertex form quadratic equation to $0$ and simplify:
$$0 = g(x+h)^2+k$$
$$\downarrow$$
$$-k = g(x+h)^2$$
$$\downarrow$$
$$\frac{-k}{g} = (x+h)^2$$
$$\downarrow$$
$$\pm \sqrt{\frac{-k}{g}} = (x+h)$$
$$\downarrow$$
$$x = -h \pm \sqrt{\frac{-k}{g}}\:[1]$$
For example, consider the vertex form quadratic function:
$$y = (x-1)^2 -9 $$
The roots are:
$$m,n = -h \pm\sqrt{\frac{-k}{g}} = -(-1) \pm\sqrt{\frac{-(-9)}{1}} $$
$$\downarrow$$
$$m,n = 1 \pm\sqrt{9} $$
$$\downarrow$$
$$m,n = 4,\: -2$$
Quadratic Formula Method, Roots of Standard Form Quadratic Functions
The easiest method for finding the roots of a quadratic equation is by using the quadratic formula. For a quadratic equation $y = ax^2 + bx + c$, the two roots $m$ and $n$ are given by the quadratic formula:
$$m,n = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$$
Derivation of Quadratic Formula, Finding Roots of Quadratic Functions
For a standard form quadratic function $y = ax^2 + bx + c$ we are seeking to find the values of $x$ such that $ax^2 + bx + c = 0$.
We start by dividing the entire equation by $a$:
$$x^2 + \frac{b}{a}x + \frac{c}{a}\: [1]$$
To simplify things for a moment, let $B = \frac{b}{a}$ and $C = \frac{c}{a}$ and substitute these into equation $[1]$:
$$x^2 + Bx + C = 0\:[2]$$
To solve for $x$, we need to get the above equation into a form we can simplify. We know vertex form quadratic equations are easy to simplify and we know how to convert a standard form quadratic equation into vertex form:
$$ax^2+bx+c \longrightarrow g(x+h)^2+k$$
$$g = a, \:h = \frac{b}{2a}, \: k = c-\frac{b^2}{4a}$$
$$x^2 + Bx + C \longrightarrow \left(x+ \frac{B}{2}\right)^2 + C-\frac{B^2}{4}\:[3]$$
Now we can set the right hand side of equation $[3]$ equal to zero and simplify:
$$\left(x+ \frac{B}{2}\right)^2 + C-\frac{B^2}{4} = 0$$
$$\downarrow$$
$$\left(x+ \frac{B}{2}\right)^2 = -C + \frac{B^2}{4}$$
$$\downarrow$$
$$\left(x+ \frac{B}{2}\right) = \pm\sqrt{ -C + \frac{B^2}{4}}$$
$$\downarrow$$
$$x= -\frac{B}{2} \pm\sqrt{ \frac{B^2}{4} -C}$$
$$\downarrow$$
$$x = -\frac{B}{2} \pm \sqrt{\frac{B^2-4C}{4}}$$
$$\downarrow$$
$$x = \frac{-B \pm \sqrt{B^2 -4C}}{2}\:[8]$$
Finally, we can substitute $B = \frac{b}{a}$ and $C = \frac{c}{a}$ into equation $[8]$:
$$x = \frac{-\frac{b}{a} \pm \sqrt{(\frac{b}{a})^2 -4\frac{c}{a}}}{2}$$
$$\downarrow$$
$$x = (\frac{a}{a})\left(\frac{-\frac{b}{a} \pm \sqrt{(\frac{b}{a})^2 -4\frac{c}{a}}}{2}\right)$$
$$\downarrow$$
$$x = \frac{-\frac{ab}{a} \pm \sqrt{a^2(\frac{b}{a})^2 -4a^2\frac{c}{a}}}{2a}$$
$$\downarrow$$
$$x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}\:[9]$$
Equation $[9]$ is called the quadratic formula. It allows us to calculate the roots for for any arbitrary quadratic equation.
For example, suppose we are given the quadratic equation:
$$ y = x^2 -2x - 8 $$
Evaluating the quadratic equation:
$$x = \frac{-(-2)\pm \sqrt{(-2)^2 -4(1)(-8)}}{2}$$
$$\downarrow$$
$$x = \frac{(2)\pm \sqrt{4 + 32}}{2}$$
$$\downarrow$$
$$x = \frac{(2)\pm \sqrt{36}}{2}$$
$$\downarrow$$
$$x = \frac{(2)\pm 6}{2}$$
$$\downarrow$$
$$x = 1\pm 3 = -2,\: 4$$
The inputs $x$ that cause $y$ to be zero are $x=4$ and $x=-2$.
Other Methods of Finding Roots
The root finding methods presented in this article aren't the only methods of solving for roots. Quadratic roots can be observed visually by plotting the function and determining the values where $y=0$.
For the example quadratic equation:
$$ y = x^2 -2x - 8 $$
The roots $x=4$ and $x=-2$ can be located graphically as shown in the below figure.
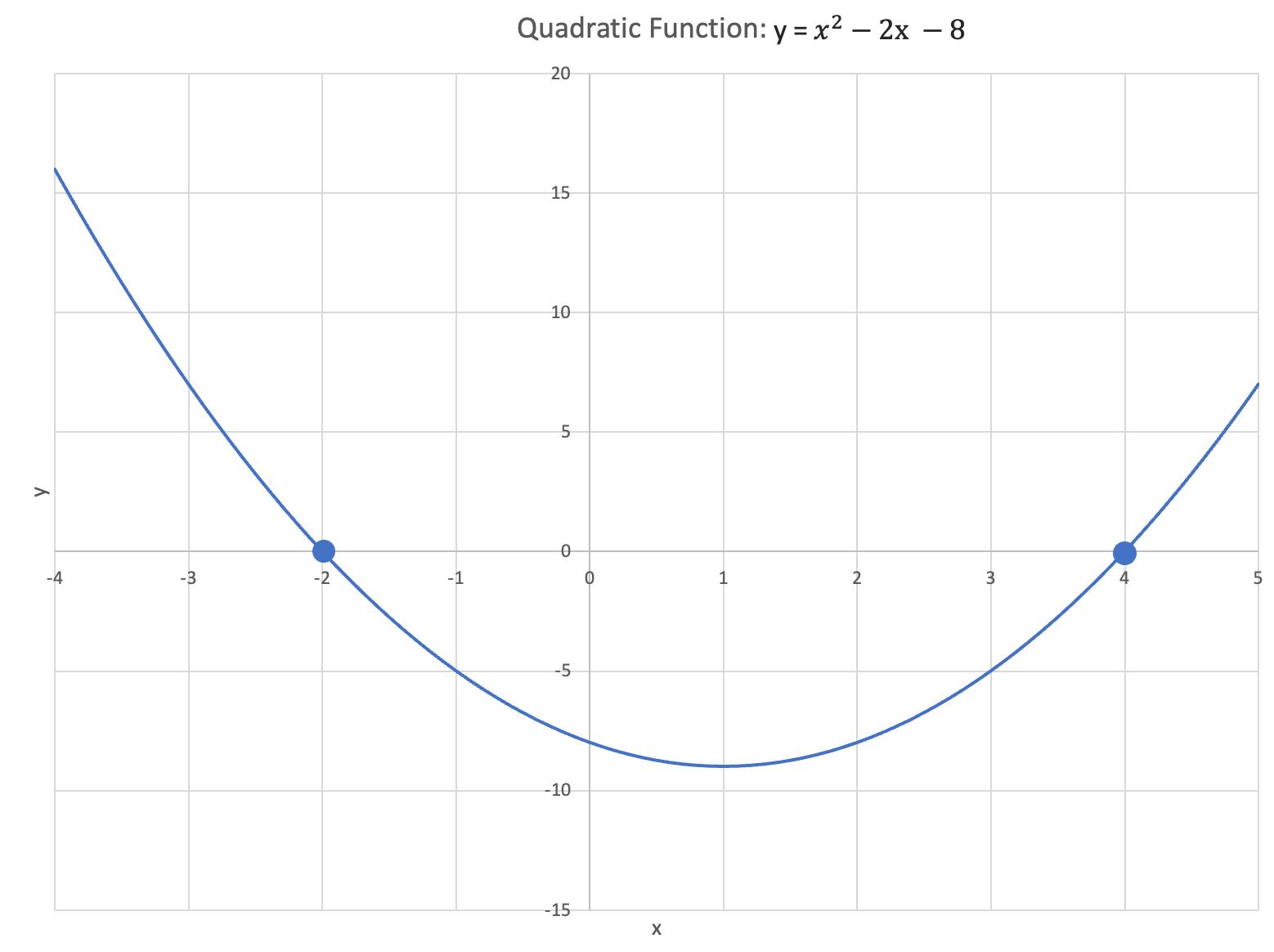
Though crude, the first quadratic root finding method typically taught is "guess and check". Math courses teaching quadratic functions often use as examples quadratic functions with small integer roots that are easy to guess and verify. After correctly guessing the roots of hundreds of simple quadratic functions, one develops an intuition for it.
There are also many general purpose root finding algorithms such as the Bisection method, Newton's method, Secant method, and more. These are algorithms that iteratively solve for the roots rather than through a direct formula. They deserve more time and attention than can be provided here so will be introduced in a future article.
Introduction to Complex Numbers
Consider the following standard form quadratic equation:
$$y = x^2 + 2x + 2$$
If we solve for the roots using the quadratic formula, we obtain the following:
$$n,m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-2 \pm \sqrt{4 - 8}}{2}$$
$$\downarrow$$
$$n,m = \frac{-2 \pm \sqrt{-4}}{2}$$
$$\downarrow$$
$$n,m = \frac{-2 \pm 2\sqrt{-1}}{2}$$
$$\downarrow$$
$$n,m = -1\pm\sqrt{-1}$$
Wait a minute... $\sqrt{-1}$!? What in the name of Darwin is that!? Some mathematicians call this a complex number while others call it an imaginary number. I don't like either term because they sound intimidating; complex numbers really aren't difficult.
Complex numbers are typically represented with the symbol $i$ or $j$:
$$i = j = \sqrt{-1}$$
Fundamentally, there is nothing wrong with the roots of a quadratic being complex. Consider the factored form of equation $y = x^2 + 2x + 2$:
$$y = (x +(1+\sqrt{-1}))(x + (1 - \sqrt{-1}))$$
We can expand it as expected to get back the standard form:
$$y = x^2 + ((1+\sqrt{-1}) + (1 - \sqrt{-1}))x + (1+\sqrt{-1})(1 - \sqrt{-1})$$
$$\downarrow$$
$$y = x^2 + 2x + (1 - \sqrt{-1} + \sqrt{-1} - (\sqrt{-1})^2)$$
$$\downarrow$$
$$y = x^2 + 2x + (1 +1)$$
$$\downarrow$$
$$y = x^2 + 2x + 2$$
Also consider if we substitute one of the roots into the standard form:
$$y = x^2 + 2x + 2$$
$$\downarrow$$
$$y = (-1 + \sqrt{-1})^2 + 2(-1+ \sqrt{-1}) + 2$$
$$\downarrow$$
$$y = (-1 + \sqrt{-1})(-1 + \sqrt{-1}) + (-2+ 2\sqrt{-1}) + 2$$
$$\downarrow$$
$$y = (1 -2\sqrt{-1} + (\sqrt{-1})^2) - 2 + 2\sqrt{-1} + 2$$
$$\downarrow$$
$$y = (1 -2\sqrt{-1} -2) + 2\sqrt{-1}$$
$$\downarrow$$
$$y = 0$$
Even though $\sqrt{-1}$ is not a regular number, it still complies to the rules of mathematics when we treat it as a number and handle it correctly.
Though they are typically introduced at the same time as quadratic functions, there is often a large time gap between first introduction and practical application. This is unfortunate, but at mechatronics.studio, we will embrace the power of complex numbers early.
Practical Applications of Quadratic Functions
Quadratic functions have a number of practical applications. Below are a couple of examples.
Trajectory of Thrown Objects
When an object is thrown, the relationship between the object's horizontal $x$ and vertical $y$ position can be described by a quadratic equation. For example, a person throws a ball at a $33.7$ degree angle relative to vertical at a speed of 36 $\frac{ft}{s}$. The initial height of the ball when thrown is $3$ feet. The relationship between the $x$ and $y$ positions of the ball is:
$$y = -\frac{32.2}{900}x^2 + \frac{2}{3}x + 3$$
Note that we have not discussed the physics of how this equation is derived, but for the moment, take a leap of faith that this is the equation that describes the $x$ and $y$ relationship of a thrown object in earth's gravity without air resistance.
A graph of the thrown ball is shown below.
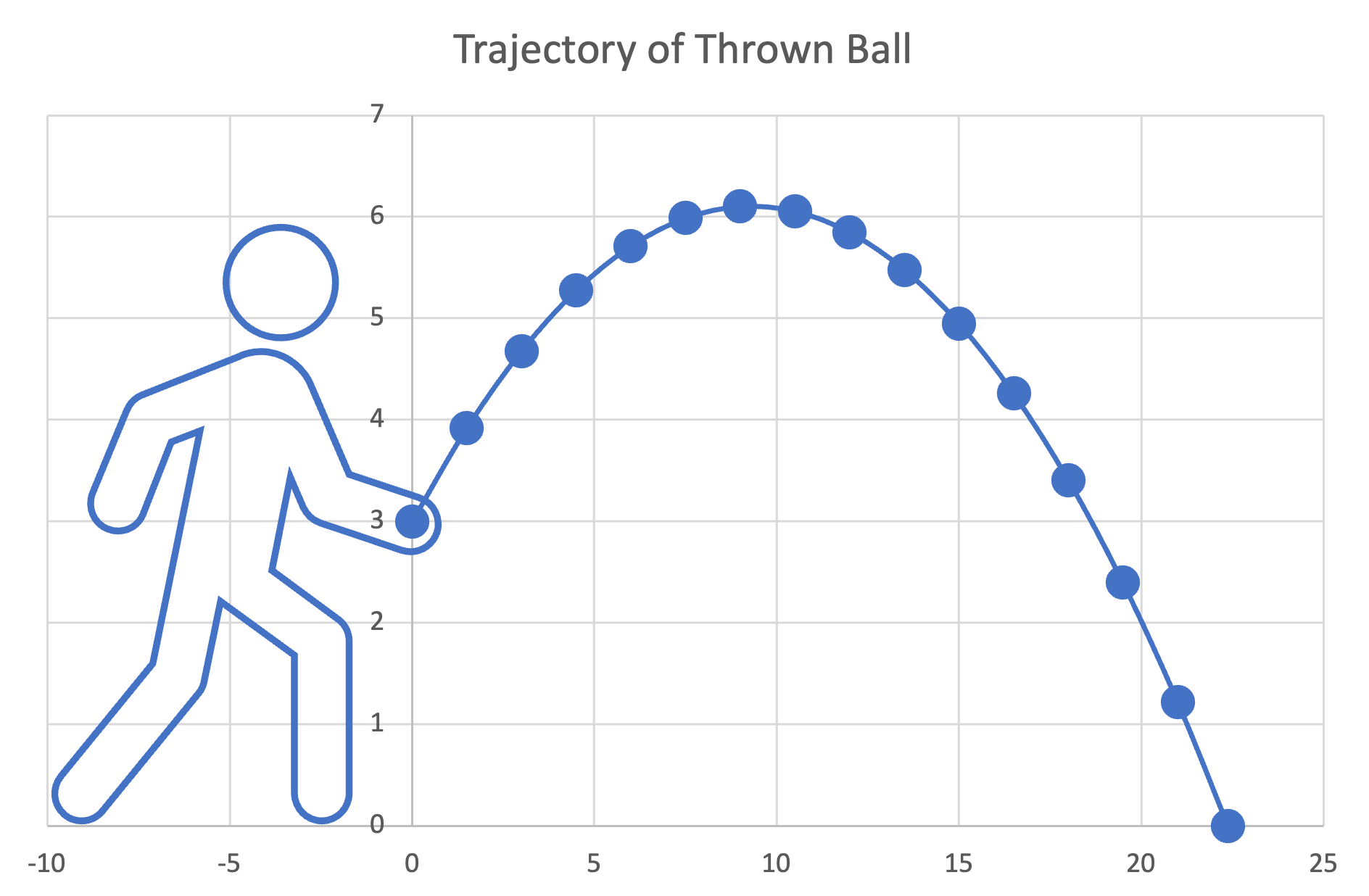
Suppose we want to know the distance the ball travels when it hits the ground, when $y = 0$. That is a root of the quadratic equation! We can solve for the roots $n$ and $m$ using the quadratic formula:
$$n,m = \frac{-\frac{2}{3} \pm \sqrt{(\frac{2}{3})^2-4(-\frac{32.2}{900})(3)}}{2(-\frac{32.2}{900})}$$
$$\downarrow$$
$$n,m = -3.75,\: 22.38$$
Clearly the negative root isn't what we are interested in so we choose the positive root and conclude that the distance the ball has traveled when it hits the ground is $22.38$ feet.
Mirrors
When light is reflected on a flat mirror, the angle of reflection is equal to the angle of incidence. Any light traveling in the same direction at the mirror will be reflected back identically.
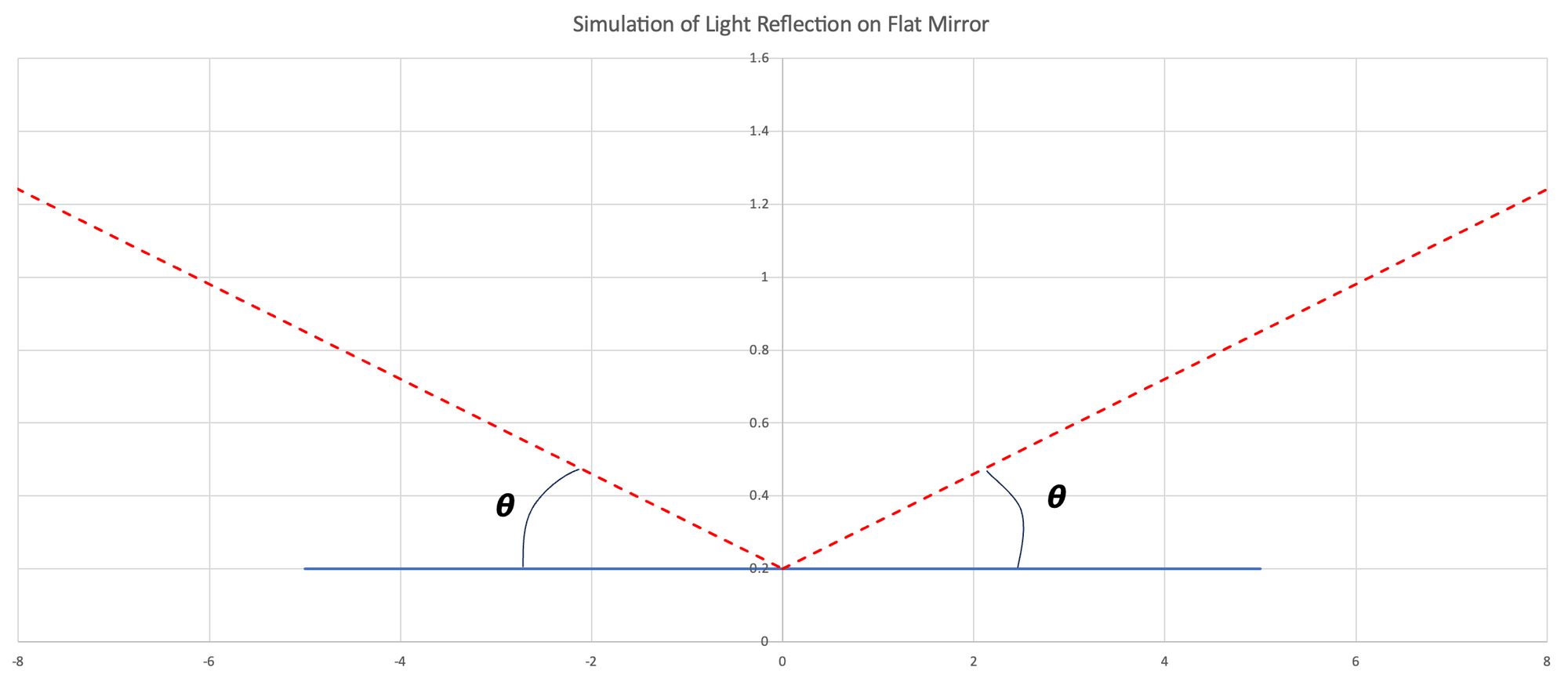
Light reflects the same way on curved mirrors, but because the surface of the mirror is curved, light traveling in the same direction is reflected at different angles depending on where the light hits the surface. Quadratic mirrors, also called parabolic mirrors, are special because all light coming from one direction is reflected to one point, the focus.
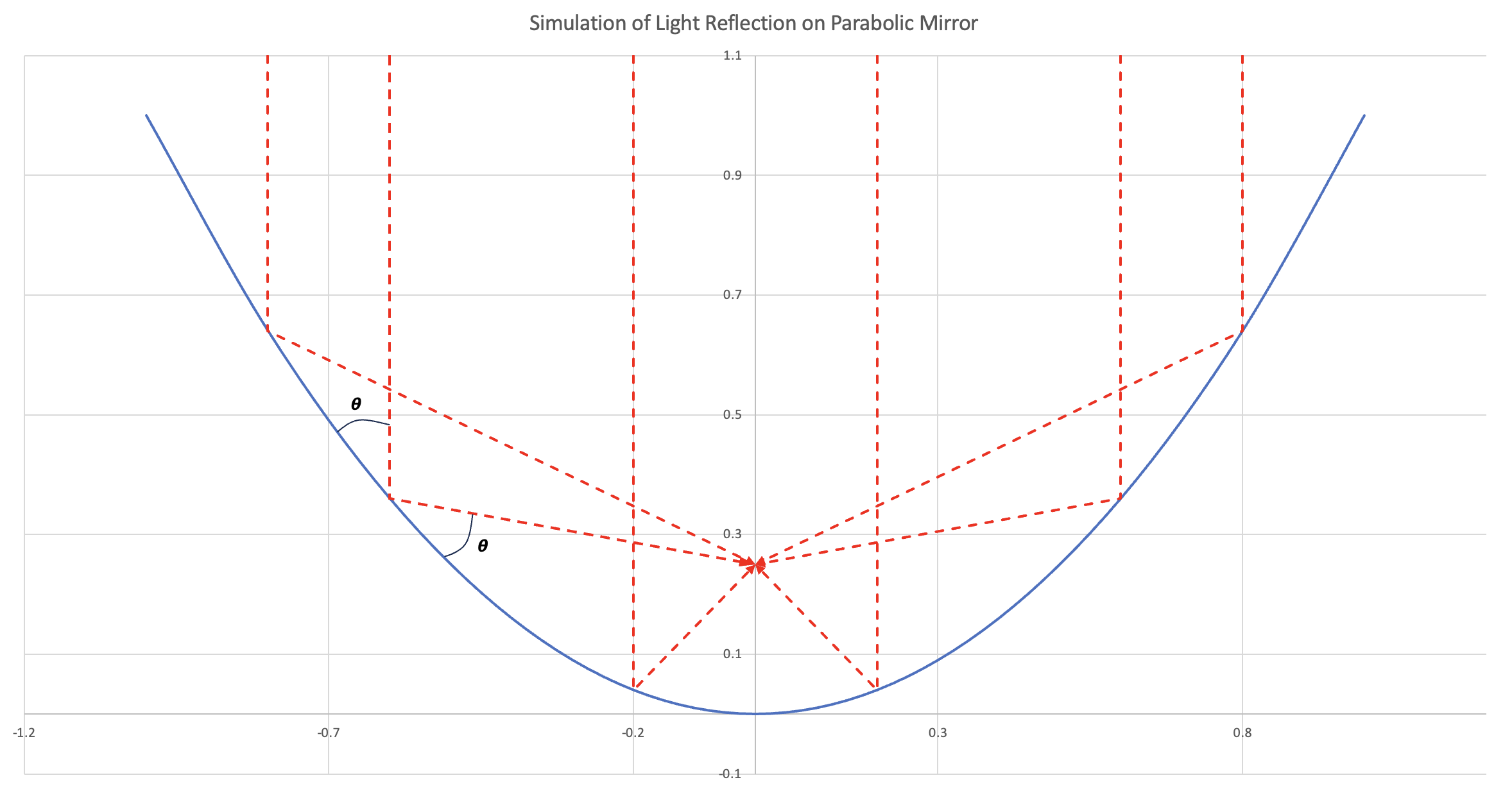
The equation for this mirror is $y = x^2$ and the focus of all the light rights is located at $x = 0$, $y = 0.25$.
One very common application of parabolic mirrors is the satellite dish, which reflects radio waves (very low frequency light waves) to a receiver.

