Mar 18, 2024 12 min read

Parametric Equations

Photo by Mateo Fernandez, courtesy of unsplash

Prerequisites- Basic Mathematics, Standard Vectors

Traditional functions of the form $y = f(x)$ accept an input $x$ and return an output $y$. When these functions are graphed, we put the input $x$ along the horizontal axis and the output $y$ along the vertical axis.

Consider the function $y = x^2$. The graph of this function is shown below:

**Figure 1:** Plot of the function $y = x^2$

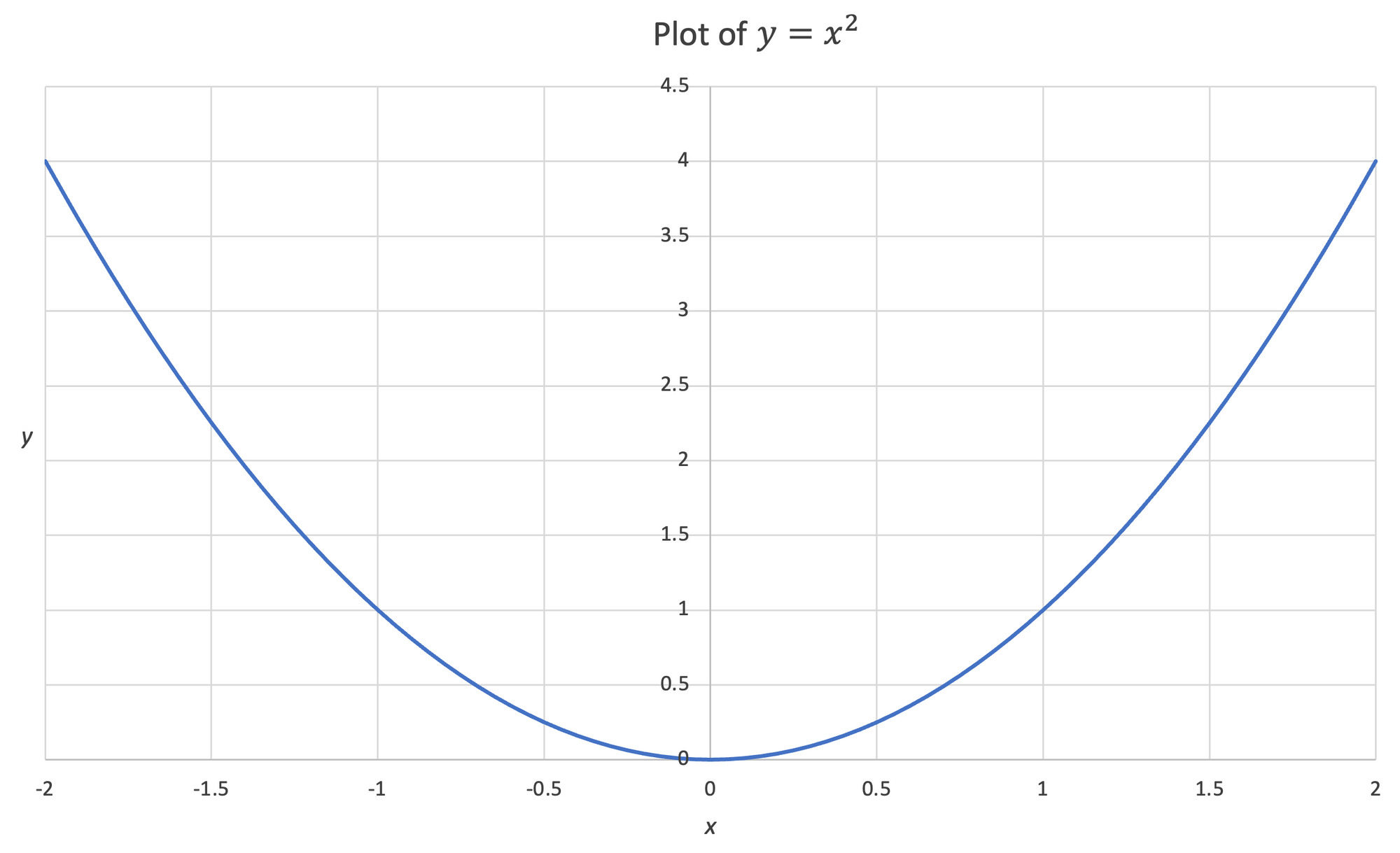
Functions are often quite aesthetic, they form all kinds of interesting shapes.

**Figure 2:** *Left-* Plot of the function $y = x^3$ | *Center-* Plot of the function $y = sin(x)$ | *Right-* Plot of the function $y = xcos(10x)$

Sometimes we desire to use functions to represent curves and paths. There are many reasons we might want to do this; architecture, motion graphics, roller coasters, civil planning, illustration, and mechanical engineering are just a few examples.

**Figure 3:** *Upper Left-* Photo of Zentrum Paul Klee, by Ricardo Gomez, courtesy of unsplash | *Upper Center-* Electrical path animation by motionstock, courtesy of pixabay | *Upper Right-* Three dimensional curves are used to design roller coasters, photo by Mateo Fernandez, courtesy of unsplash | *Lower Left-* Curves are used to plan roads, photo by David Talley, courtesy of unsplash | *Lower Center-* Digital illustrations can be created using curves, by cromaconceptovisual, courtesy of pixabay | *Lower Right-* Curves are used extensively in mechanical engineering design, by PIRO4D, courtesy of pixabay

I don't think I can overstate how important curves are. Though the value of using math to draw curves is not often emphasized in math courses, very few of our modern advancements would be possible without them.

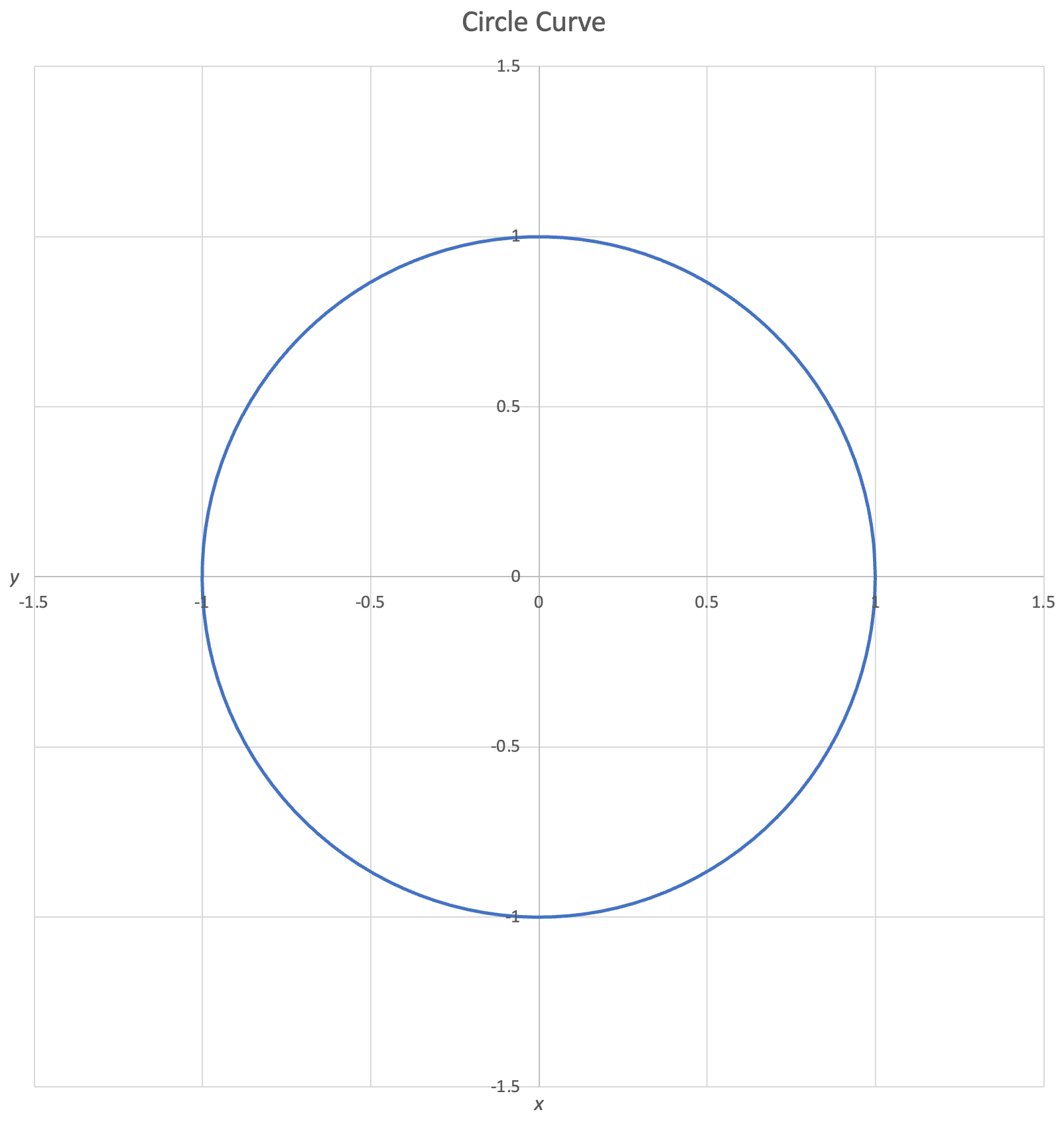
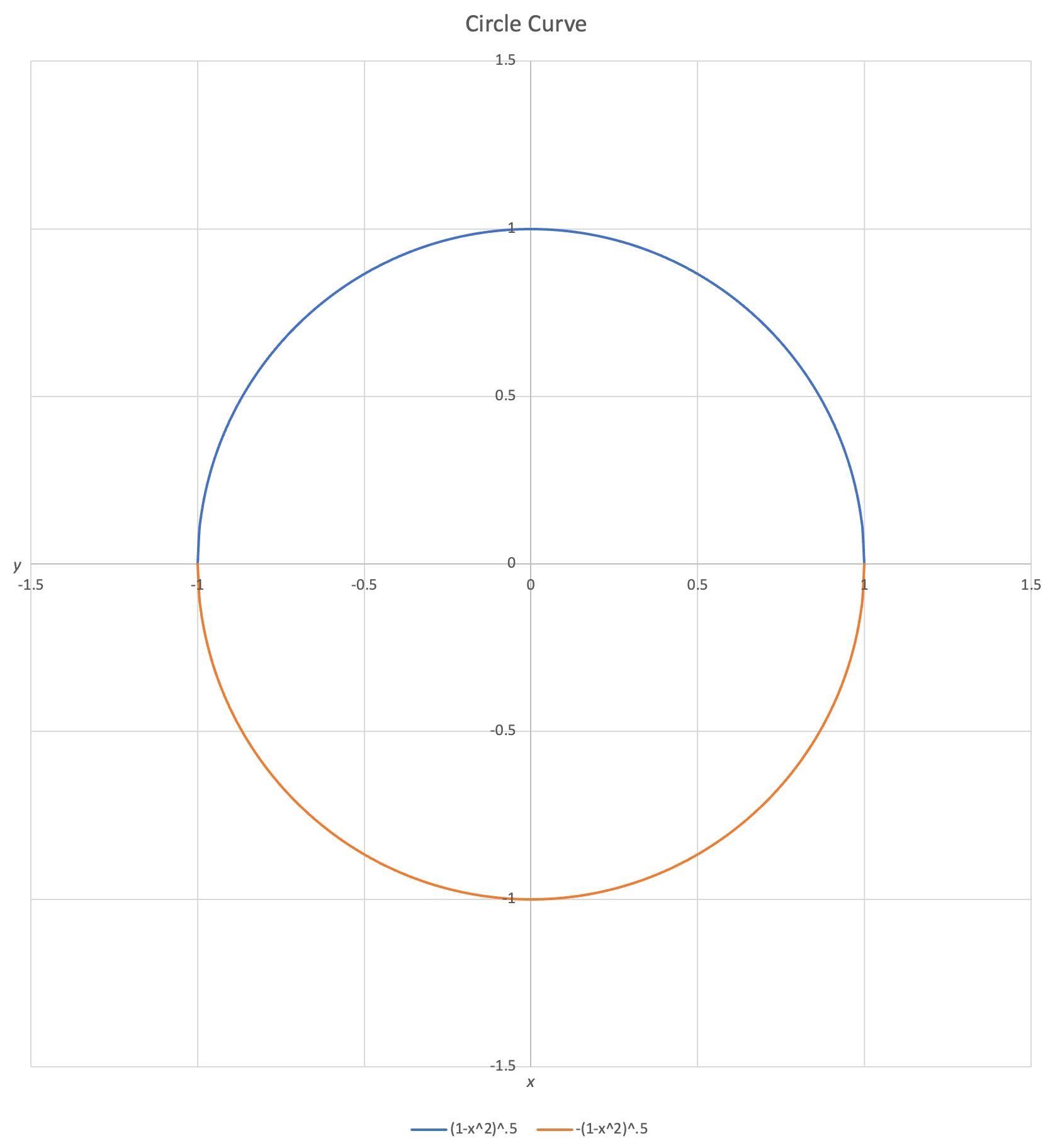
One means of creating curves from traditional functions $y = f(x)$ is to stitch together multiple functions to draw a shape. The below equation creates a circle by stitching together two semicircles:

$$y = \begin{cases} \sqrt{1-x^2} \\ -\sqrt{1-x^2}\end{cases},\: -1 \le x \le 1$$

If we plot this equation, we obtain the below curve:

**Figure 4:** Plot of two semi-circle functions stitched together to form a full circle.

Stitching makes it possible to draw many kinds of curves, but there is an unfortunate difficulty involved. For each function, each input $x$ corresponds to just one output $y$. This makes it challenging to draw certain curves. Any curve that reverses in $x$ must be represented by a stitched function broken up where the tangent is vertical.

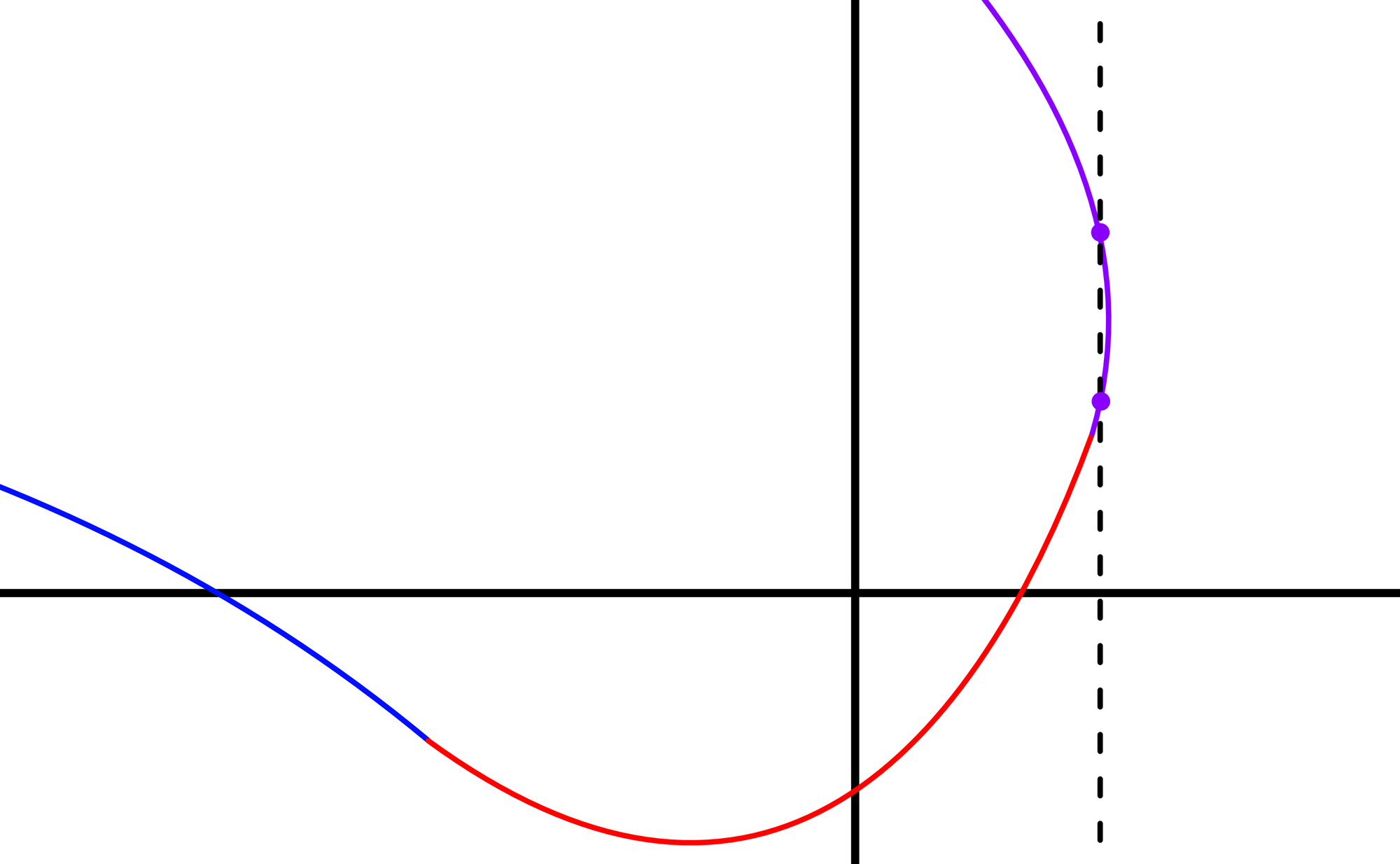
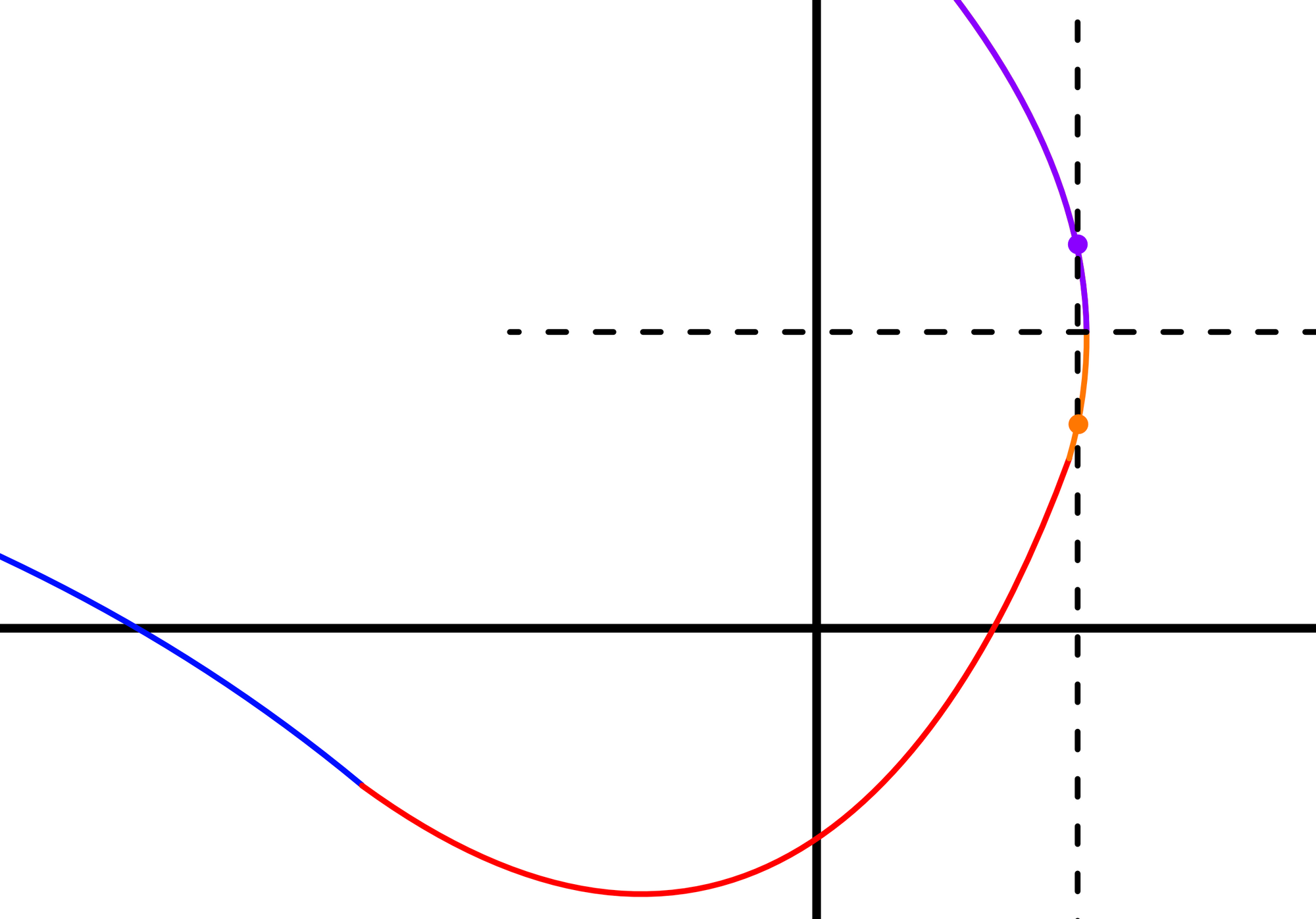
**Figure 5:** A chain of functions is being used to draw an interesting curve. | *Left-* This chain is invalid because the purple function has multiple $y$ values for some $x$ values | *Right-* This chain is valid. Each function contains only one output $y$ for each input $x$.

This is all rather complicated. Instead of representing paths as stitched functions $y = f(x)$, an alternative would be to introduce a new variable $s$ and define both $x$ and $y$ as functions of $s$:

$$x = f(s),\: y = g(s)$$

This is called a parametric equation. Some educational resources choose to use the letter $t$ to represent the parameter rather than $s$ but because $t$ is often associated with time, I prefer $s$.

If we wanted to represent a circle using a parametric equation, we could use the below function:

$$x = cos(s),\: y = sin(s)$$

For this equation, a plot of $y$ vs $x$ is shown below:

Jonathan Bowen