Exponential Arithmetic

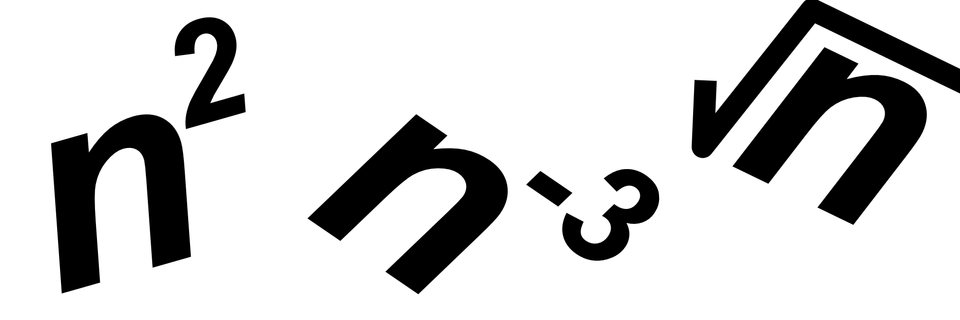
Before coming to this blog, I assume you have learned the fundamentals of basic arithmetic (addition, subtraction, multiplication, and division of numbers). $4+4=8$, $10∗6=60$, $7−3=4$, and $\frac{12}{2}=6$ should all be very comfortable to calculate. When it’s $11:37\small{AM}$ and you calculate there are $23$ minutes until lunch at noon you have used arithmetic. When someone hands you a five dollar bill for a $\$4.75$ churro, you hand them $\$0.25$ back and have done arithmetic.

Exponentiating Numbers

Less common in daily experience is exponential arithmetic. We can write two times two as $2*2$, but we can also write it using exponential notation, $2^2$. This is called squaring a number. In this example, we call this, "two squared".

We can square any number we desire:

$$3*3 = 3^2,\ 6*6 = 6^2$$

When we multiply three copies of a number, it is called cubing:

$$3*3*3 = 3^3,\ 6*6*6= 6^3$$

In general, we can multiply as many copies of a number that we want, this is called exponentiation. A base number $b$ is exponentiated by raising it to some power $p$:

$$b^p$$

For the exponentiated number below, $4$ is the base, $8$ is the power:

$$4^8$$