Introduction to Derivatives
Prerequisites Required- Basic Mathematics
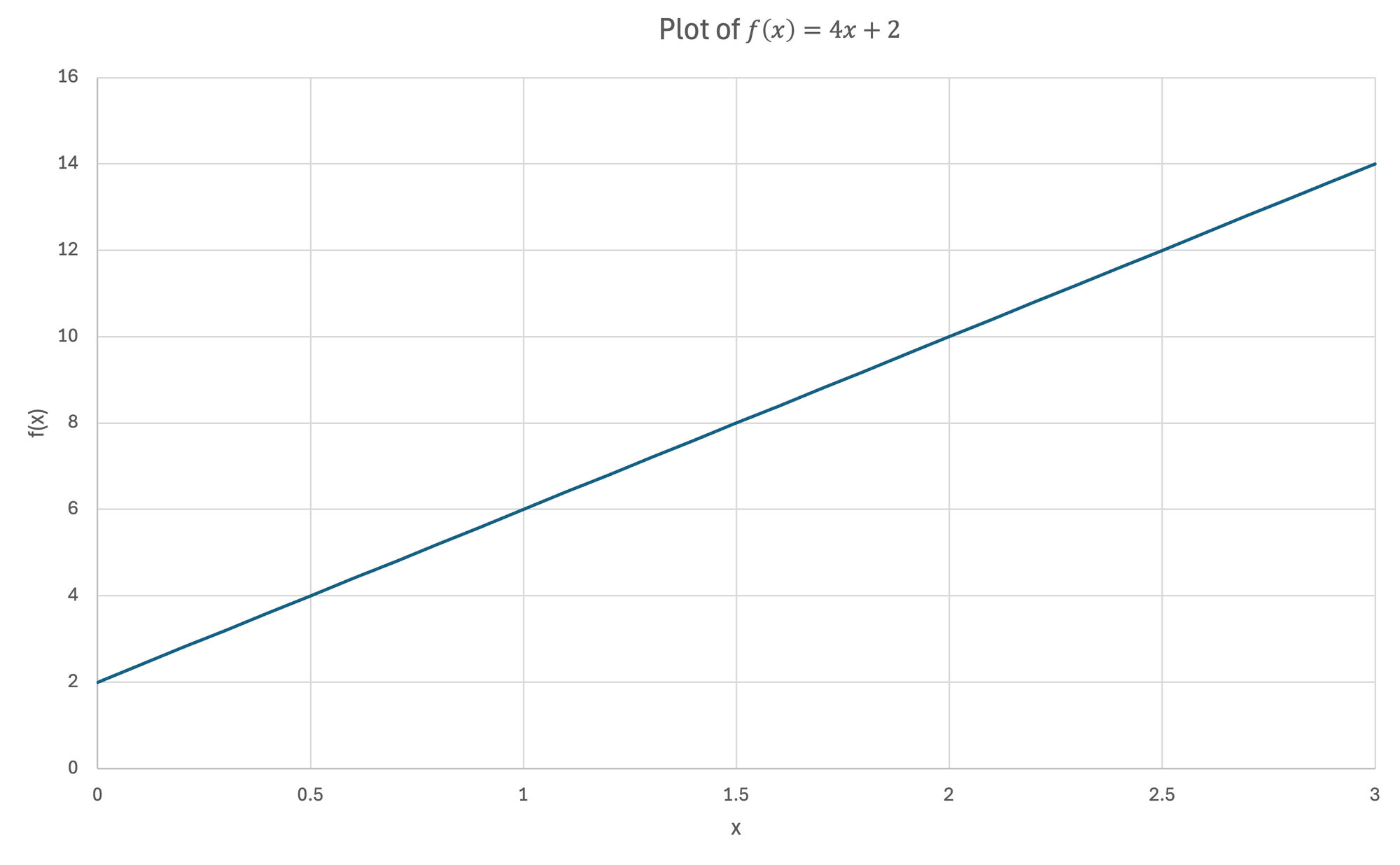
Suppose we have a basic linear function, $f(x) = 4x + 2$
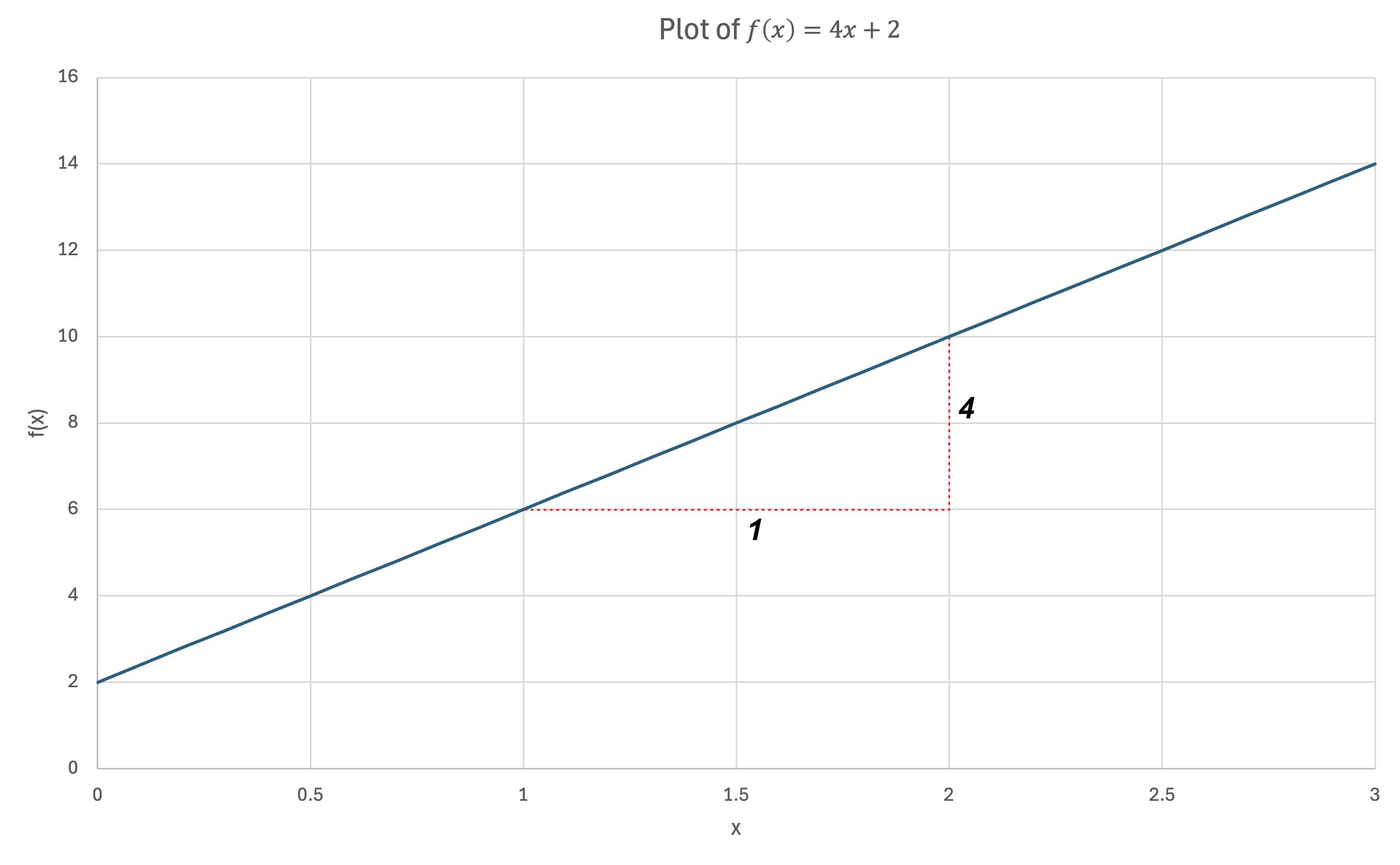
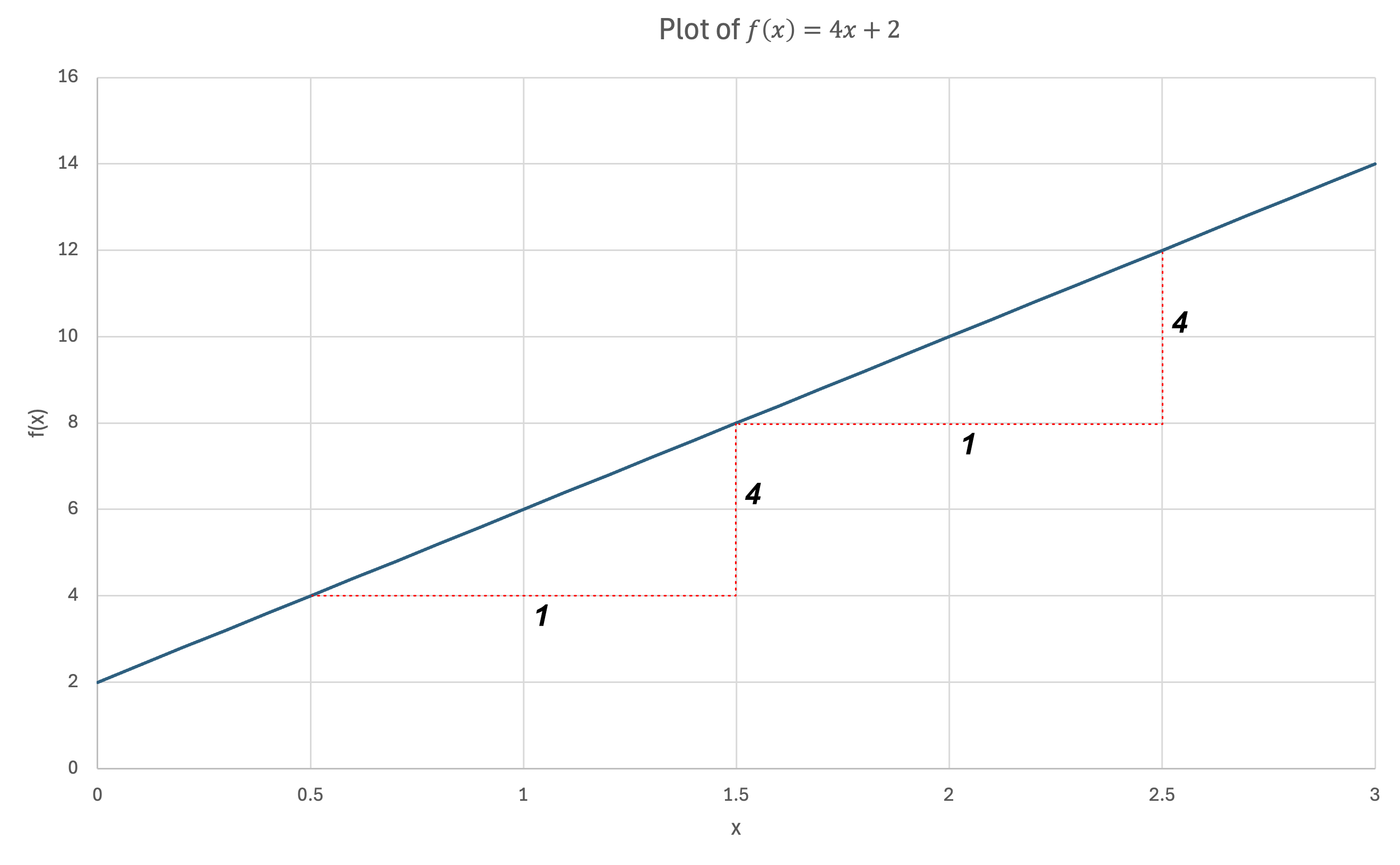
The slope of this function is $4$ (if the input $x$ increases by 1, the output increases by $4$).
The derivative of a function is its slope (change in output per change in input). This calculation is very easy for linear functions because the slope is the same everywhere.
For the function $f(x) = 4x + 2$, its slope with respect to $x$ is 4.
For the function $f(g) = 3g + 1$, its derivative with respect to $g$ is 3.
For functions containing multiple variables, calculating the slope with respect to one variable is done by regarding the other variables as similar to constants.
For the function $f(x,k) = 2x + 6k^2 + 4$, its derivative with respect to $x$ is 2.
Mathematical Notation for Derivatives
Mathematicians, physicists, and engineers have developed many methods of symbolizing derivatives. The different notations have situationally dependent benefits.
One common method of symbolizing derivatives is by appending the apostrophe $'$ symbol to the function. For our basic linear function $f(x) = 4x + 2$, the derivative $f'(x)$ is:
$$f'(x) = 4$$
In conversation, $f'(x)$ is communicated as "f prime of x". The use of the apostrophe is typically limited to functions with only one variable because otherwise it is not clear which variable we are taking the derivative of.
For example, suppose we have the function $f(y, z) = 4y + 2z + 6$. What is $f'(y,z)$? Unknown. It's ambiguous.
Another way of symbolizing the derivative is by prepending the function with $\frac{d}{dv}$ where $v$ is the variable we are taking the derivative with respect to. For the variable $x$, we symbolize the derivative with $\frac{d}{dx}$. For the function $f(x) = 4x + 2$, the derivative is:
$$\frac{d}{dx} f(x) = 4$$
We are not limited to the variable $x$. There is no reason we couldn't have a function $f(z) = 4z + 2$ and determine the derivative with respect to $z$:
$$\frac{d}{dz} f(z) = 4$$
This notation is less ambiguous than the apostrophe notation. Suppose we have a function $f(y, z) = 4y + 2z + 6$. The derivative with respect to $y$ is:
$$\frac{d}{dy} f(y, z) = 4$$
A similar method to symbolize a derivative is to cram the function symbol into the numerator. For the function $f(x) = 4x + 2$, its derivative with respect to $x$ can by symbolized as $\frac{df}{dx}$. For the function $f(x) = 4x + 2$, the derivative is:
$$\frac{df}{dx} = 4$$
It is common to symbolize the derivative of a function with respect to time $t$ by placing a dot above the function. For example, the time derivative of $f(t) = 4t + 2$ is:
$$\dot{f}(t) = 4$$
Because the dot notation is only for derivatives with respect to time, this notation is often used for functions with multiple variables (one of them being time). Suppose we have a function $f(t, z) = 4t + 2z + 6$. The derivative of this function with respect to $t$ is:
$$\dot{f}(t, z) = 4$$
Mathematical Notation for Higher Derivatives
We are not limited to taking a single derivative of a function. We can determine the derivative of a function's derivative, which is the 2nd order derivative of the function. The derivative of the 2nd order derivative is the 3rd order derivative of the function. This continues on for as many derivatives as we desire to calculate.
For the apostrophe notation, the 2nd order derivative is written by stacking another apostrophe after the first:
$$f''(x)$$
The 3rd order derivative is written by further apostrophe stacking:
$$f'''(x)$$
For the fractional notation, exponentials are used. The 2nd order derivative is written as:
$$\frac{d^2}{dx^2}f(x) \:or\: \frac{d^2 f}{dx^2}$$
The 3rd order derivative is written as:
$$\frac{d^3}{dx^3}f(x) \:or\: \frac{d^3 f}{dx^3}$$
For the dot notation, multiple dots are used. The 2nd order derivative is written as:
$$\ddot{f}(t)$$
The 3rd order derivative is written as:
$$\dddot{f}(t)$$
From here, the pattern for symbolizing derivatives beyond the 3rd order should be clear.
Estimating the Derivative
The derivative is simply the slope of the function, rise over run. For linear functions, this is easy because the slope of a linear equation is the same value everywhere and is easy to calculate.
For non-linear functions like $f(x) = x^2$ however, the slope of the function changes depending on the value of the input $x$.
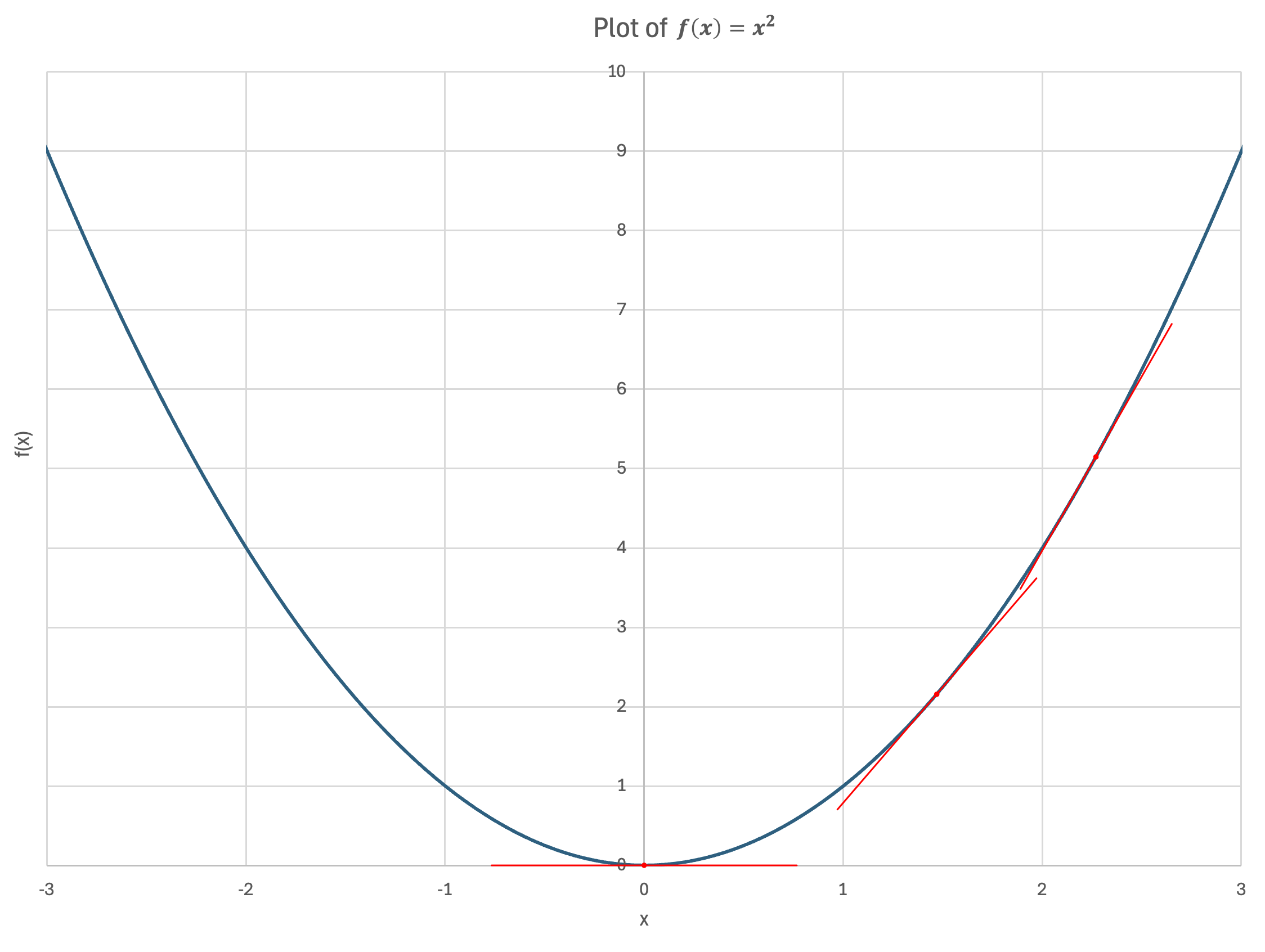
We can estimate the value of the derivative by a forward difference derivative approximation. For a function $f(x)$ and a value $h$, the derivative is approximated by:
$$f'(x) \approx \frac{f(x+h) - f(x)}{h}$$
Derivative of $f(x) = x^2$
Let's consider the quadratic equation $f(x) = x^2$.
We will start by finding the derivative of the function at $x = 2$.
We will estimate the derivative for $h = 1$, $h = 0.5$, and $h = 0.25$.
$$f'(x = 2, h = 1) = \frac{f(x+h) - f(x)}{h} = \frac{(2 + 1)^2 - 2^2}{1} = \frac{9 - 4}{1} = 5 $$
$$f'(x = 2, h = 0.5) = \frac{f(x+h) - f(x)}{h} = \frac{(2 + 0.5)^2 - 2^2}{1} = \frac{6.25 - 4}{0.5} = 4.5 $$
$$f'(x = 2, h = 0.25) = \frac{f(x+h) - f(x)}{h} = \frac{(2 + 0.25)^2 - 2^2}{1} = \frac{5.0625 - 4}{0.25} = 4.25 $$
If we plot a line through the point $\big(2,f(2) \big)$ and $\big( 2+h,f(2+h) \big)$ for each estimate, we obtain the below graphs:
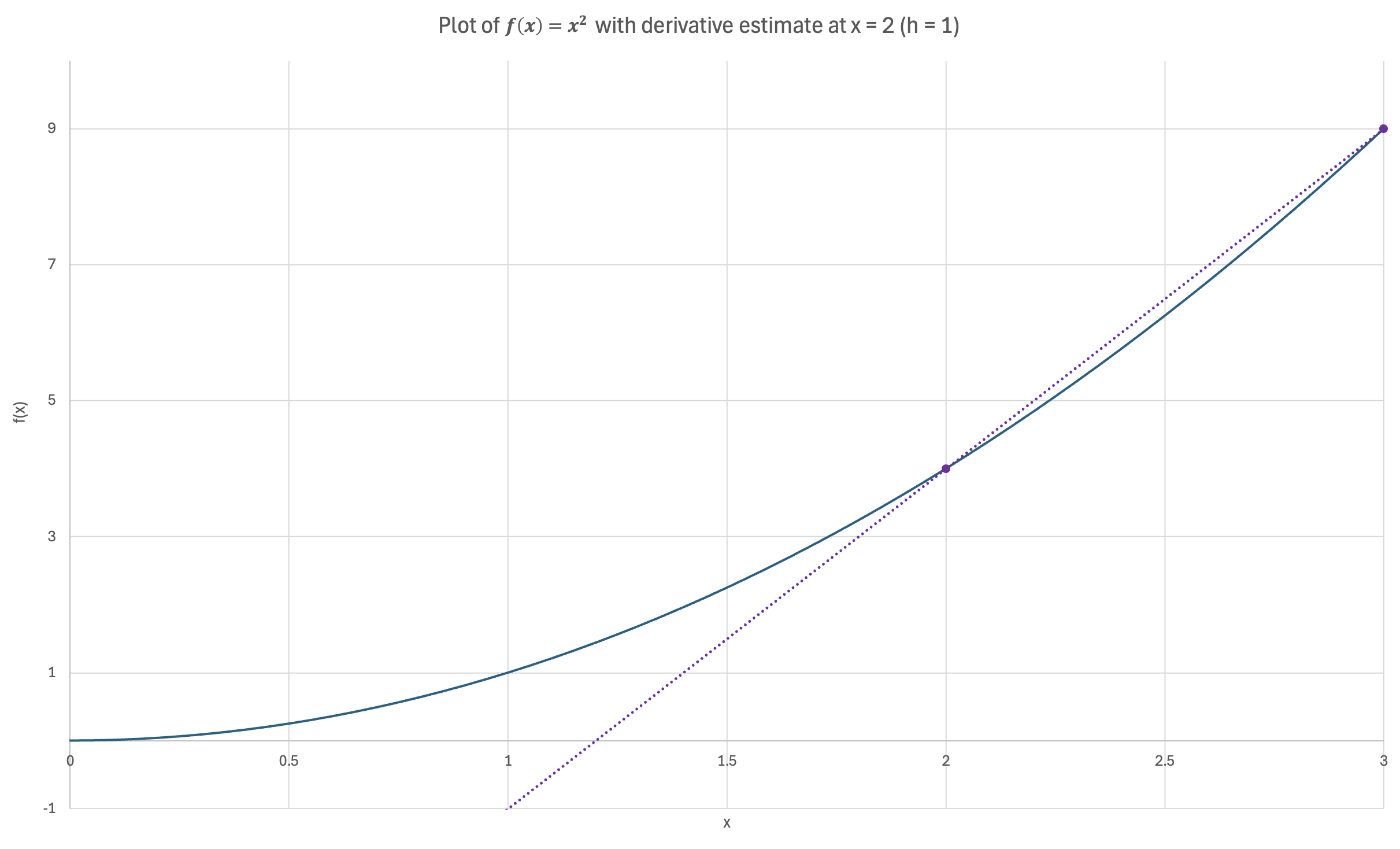
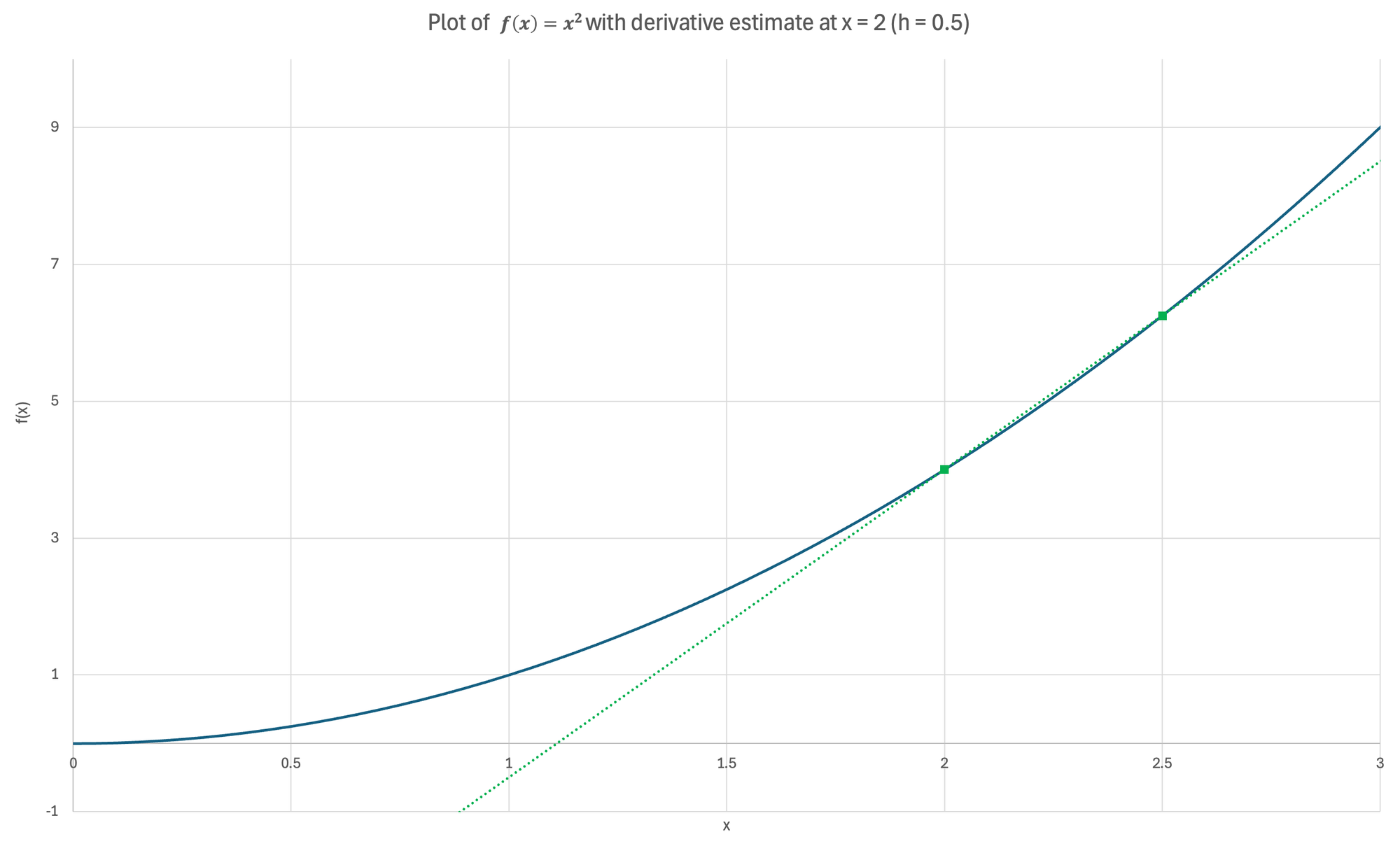
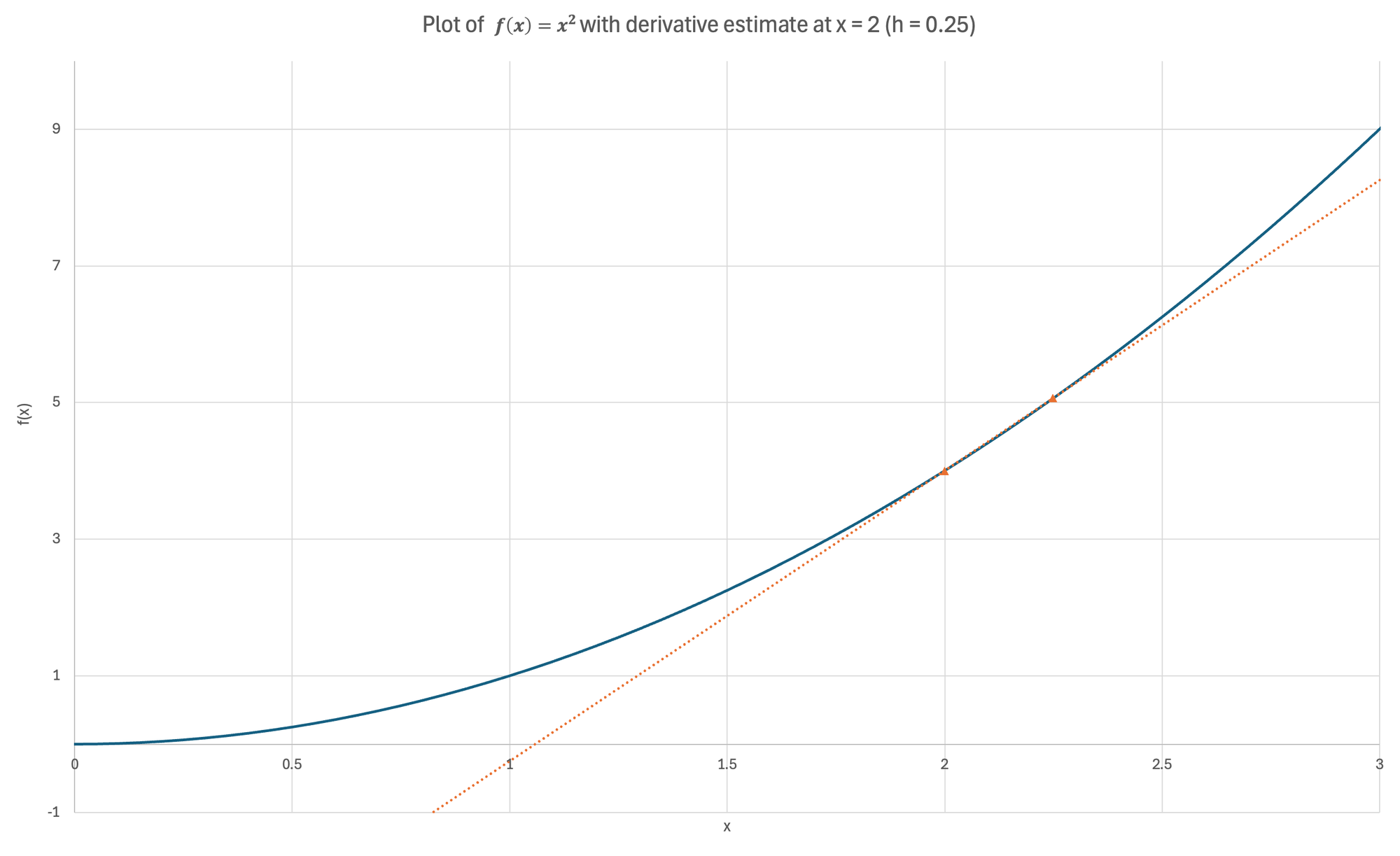
Figure 6: Visual demonstration of estimating the derivative using a forward difference Left- Derivative estimate for $h = 1$| Center- Derivative estimate for $h = 0.5$ | Right- Derivative estimate for $h = 0.25$
Visually, we can see that as $h$ becomes smaller, the estimated slope is a better approximation for the actual slope of the function. However, we can't just substitute $h = 0$ into our estimate:
$$f'(x = 2, h = 0) = \frac{f(x+h) - f(x)}{h} = \frac{(2 + 0)^2 - 2^2}{0} = \frac{0}{0} = indeterminate$$
Instead, we need to determine the value the estimate converges to as $h$ becomes increasingly small. This is called a limit.
The true slope is the slope as $h$ becomes very near $0$ but not actually equal to zero (since this would be indeterminate).
$$f'(x = 2) = lim_{h \rightarrow 0} \frac{f(2+h) - f(2)}{h} = lim_{h \rightarrow 0} \frac{(2 + h)^2 - 2^2}{h}$$
If we were to continue decreasing $h$ and estimate the slope numerically, we find that the slope converges to $4$.
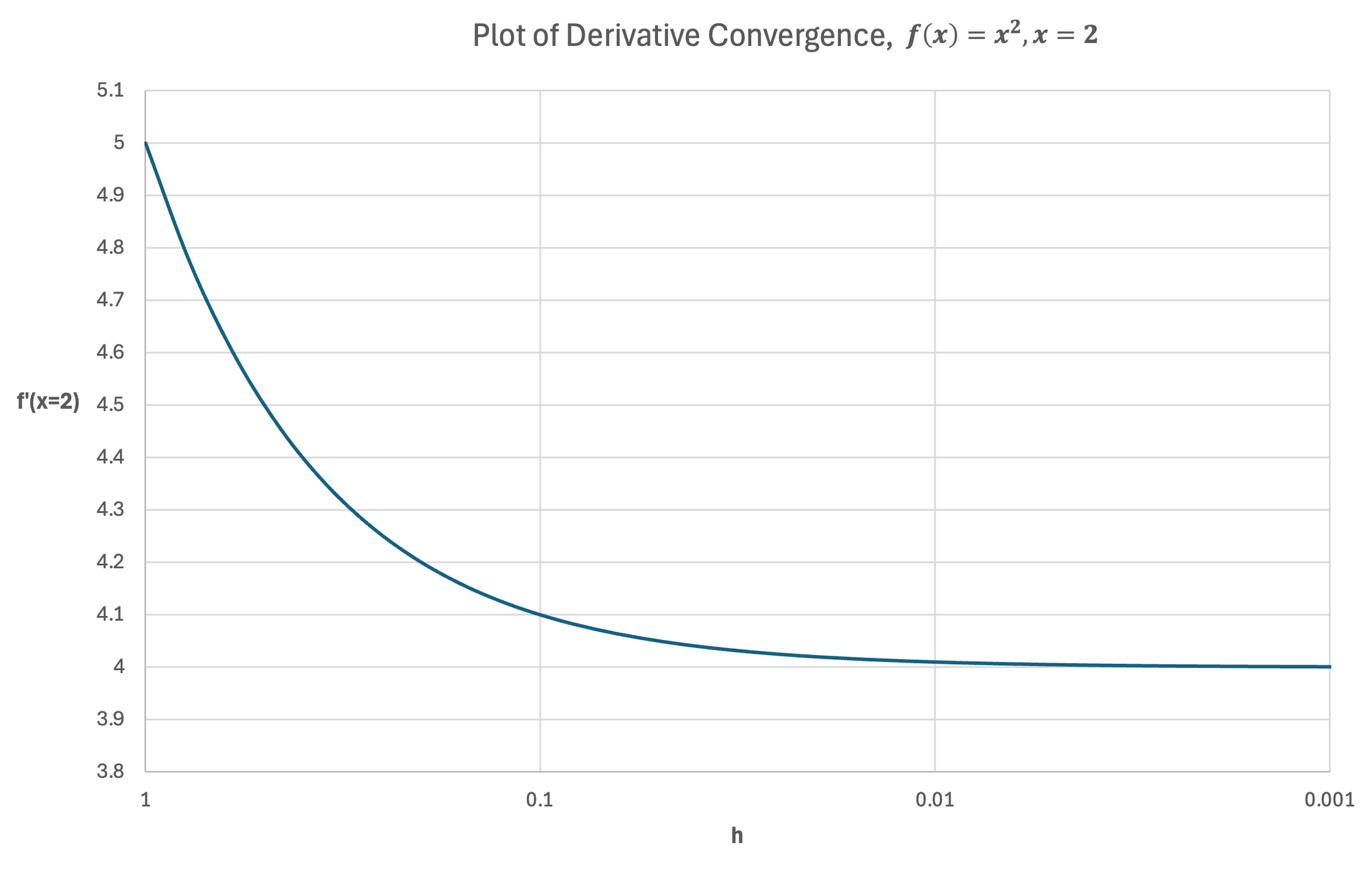
While this is certainly a valid method of calculating the derivative, it is quite unwieldy. It is possible to symbolically calculate the derivative without a numerical convergence study.
For the example $f(x) = x^2$, we calculate this limit as follows:
$$f'(x = 2) = lim_{h \to 0} \frac{(2 + h)^2 - 2^2}{h}$$
$$\downarrow$$
$$f'(x = 2) = lim_{h \to 0} \frac{(2^2 + 4h + h^2) - 2^2}{h}$$
$$\downarrow$$
$$f'(x = 2) = lim_{h \to 0} \frac{4h + h^2}{h}$$
$$\downarrow$$
$$f'(x = 2) = lim_{h \to 0} (4 + h)$$
Now, as $h$ becomes increasingly small, $(4 + h)$ converges to $4$:
$$f'(x = 2) = lim_{h \to 0} (4 + h) = 4$$
Through the same mechanism, it is possible to calculate the derivative for any arbitrary input value $x$:
$$f'(x) = lim_{h \to 0} \frac{(x + h)^2 - x^2}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{(x^2 + 2xh + h^2) - x^2}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{2xh + h^2}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} (2x + h)$$
Now, as $h$ becomes increasingly small, $(2x + h)$ converges to $2x$:
$$f'(x) = lim_{h \to 0} (2x + h) = 2x$$
When $x = 2$, $f'(x) = 4$.
When $x = 0$, $f'(x) = 0$ (by inspection, we can see that the slope is a flat horizontal line at $x = 0$, which corresponds to a slope of $f'(x) = 0$.
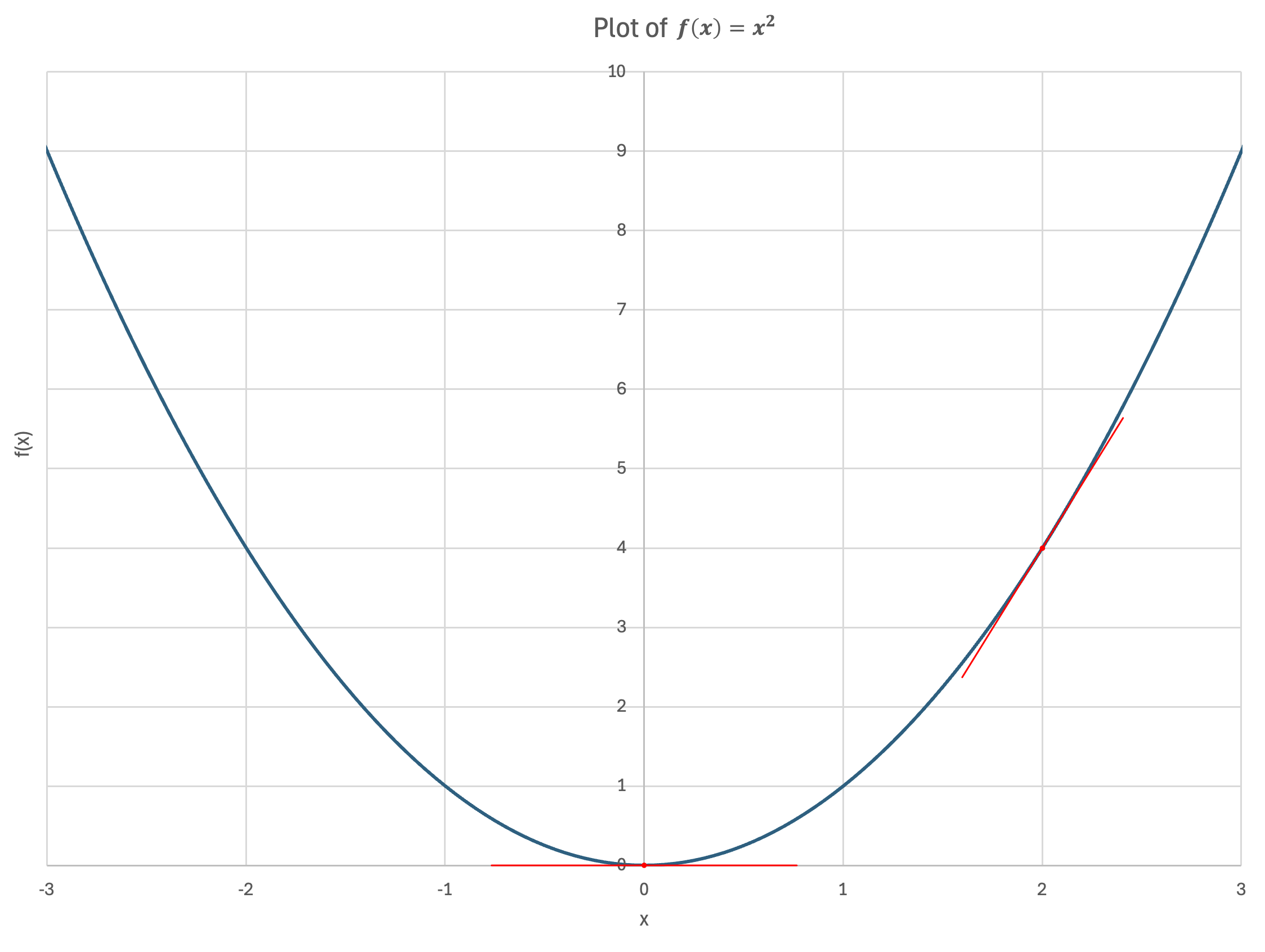
We have here symbolically the slope of the function $f(x) = x^2$ at any value of $x$!
Derivative of Arbitrary Quadratic Functions
For quadratic equations of the form $f(x) = ax^2 + bx + c$ where $a, b, c$ are numbers, finding the derivative is more laborious. Recall our definition of the derivative using a limit driven estimate:
$$f'(x) = lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$$
Substituting:
$$f'(x) = lim_{h \to 0} \frac{(a(x+h)^2 + b(x+h) + c - (ax^2 + bx + c)}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{(a(x+h)^2 + b(x+h) + c - ax^2 - bx - c}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{(a(x^2 + 2xh + h^2) + bx + bh - ax^2 - bx}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{ax^2 + 2axh + ah^2 + bh - ax^2}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} \frac{2axh + ah^2 + bh}{h}$$
$$\downarrow$$
$$f'(x) = lim_{h \to 0} (2ax + b + h) = 2ax + b$$
For any quadratic $f(x) = ax^2 + bx + c$, its derivative is $f'(x) = 2ax + b$.
In our earlier case where $f(x) = x^2$, $a = 1$, $b = 0$, and $c = 0$ so $f'(x) = 2x$, which matches our earlier result.
For the linear function case $f(x) = mx + y_0$ where $a = 0$, $b = 1$, $c = y_0$, the derivative is the constant $f'(x) = m$, which matches our earlier result.
Derivatives of Arbitrary Polynomial Functions
Through a very similar process to the quadratic function, we can calculate that the derivative for any arbitrary polynomial function $f(x) = ax^n$ is $f'(x) = anx^{n-1}$.
The derivative of the sum of any $n$ arbitrary polynomial functions $f(x) = \sum_{i=1}^n a_ix^i$ is similarly $f'(x) = \sum_{i = 2}^n a_i(i)x^{i-1}$.
For example, consider the polynomial:
$$f(x) = 4x^5 + 2x^4 + 3x^2 + 7x + 1$$
Its derivative is:
$$f'(x) = 20x^4 + 8x^3 + 6x + 7$$
Derivatives of Other Functions
The strategy outlined in this article for polynomial functions is largely the same we will employ for other functions (trigonometric, exponential, etc.), however, they are more difficult to calculate. In future articles, we will explore and calculate the derivatives of other functions.
