Introduction to Field Theory

Prerequisites Required- Basic Mathematics, Standard Vectors
Today's topic is fields.

Nope, not that kind of field; mathematical fields. Fields are actually very basic. A field consists of a property that is mapped over space (in one or more dimensions).
A Note on Symmetry and Invariance
The concept of symmetry is very useful in studying and classifying fields. To be symmetric means that if you transform an object, it is indistinguishable from the untransformed version of that same object. To be symmetric with respect to a transformation is to also be invariant to that transformation.
Below are several examples:
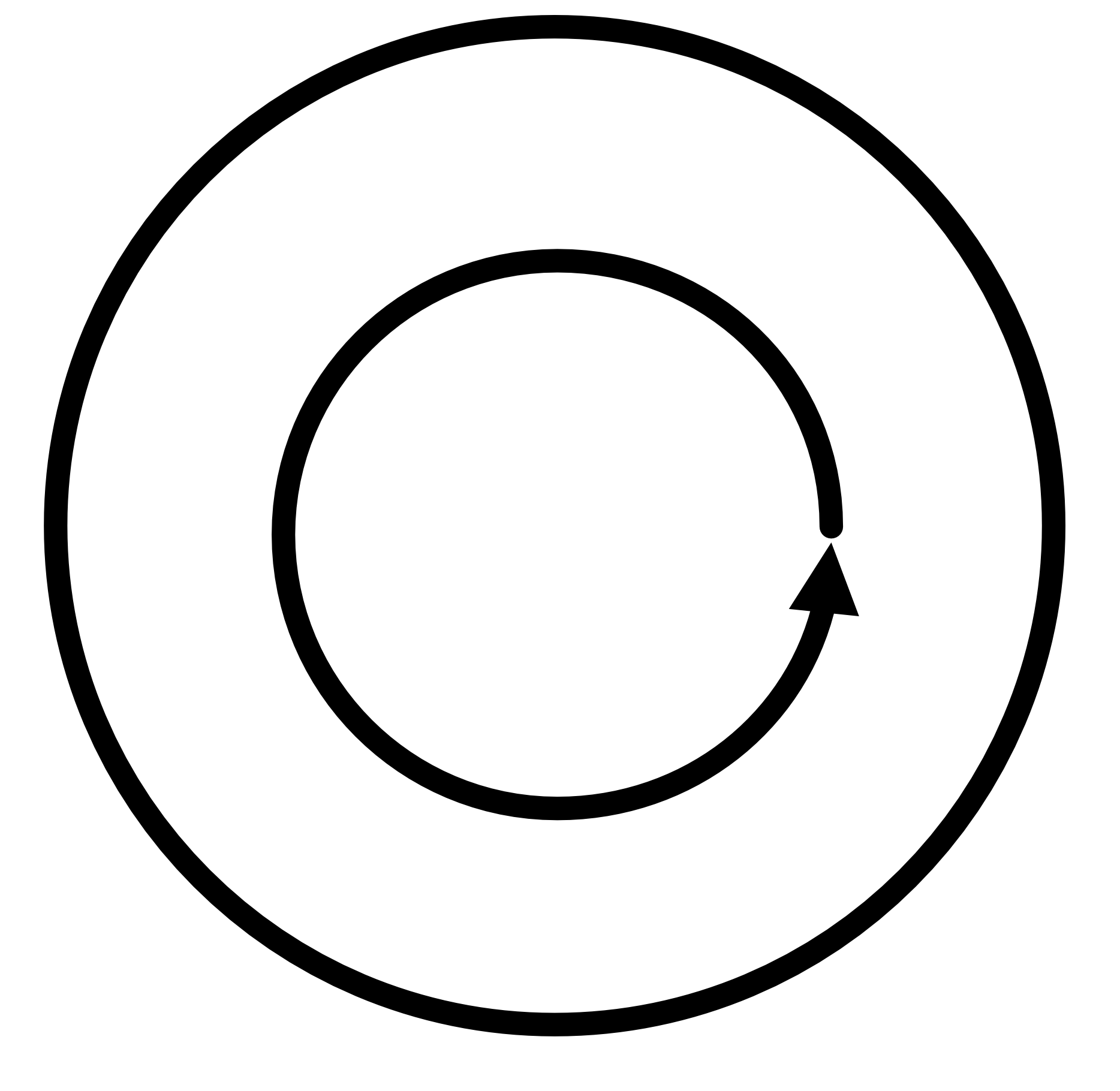
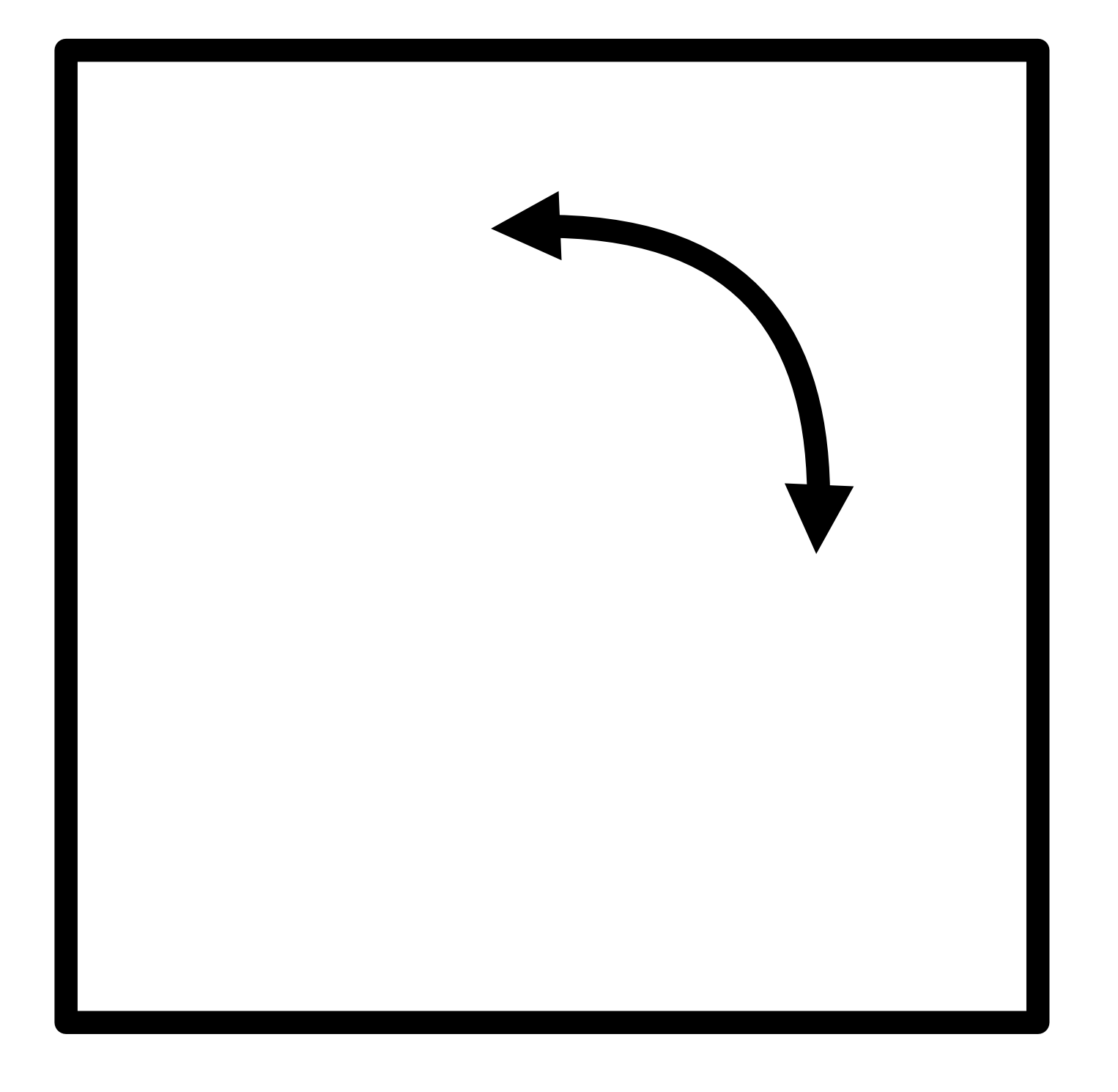
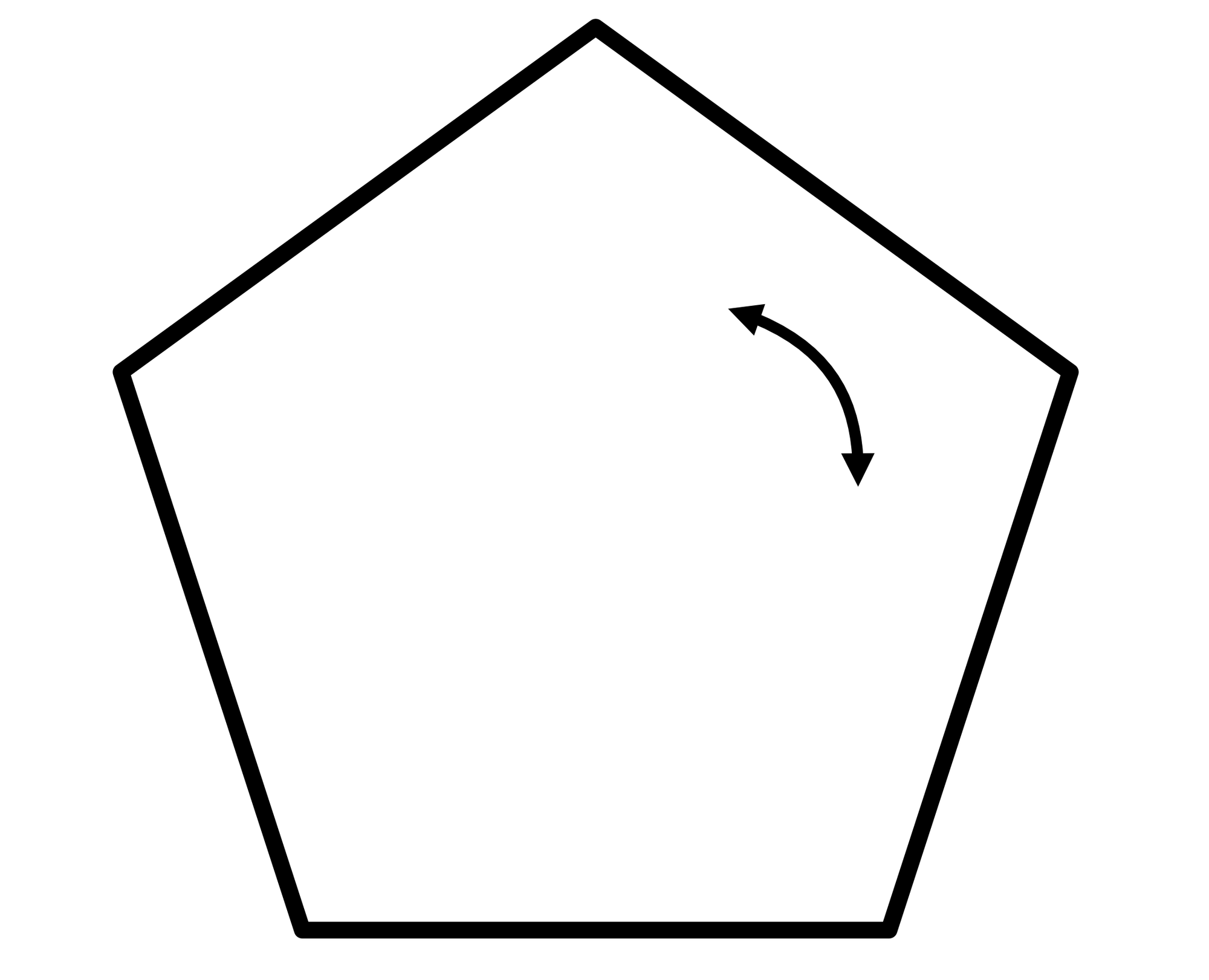
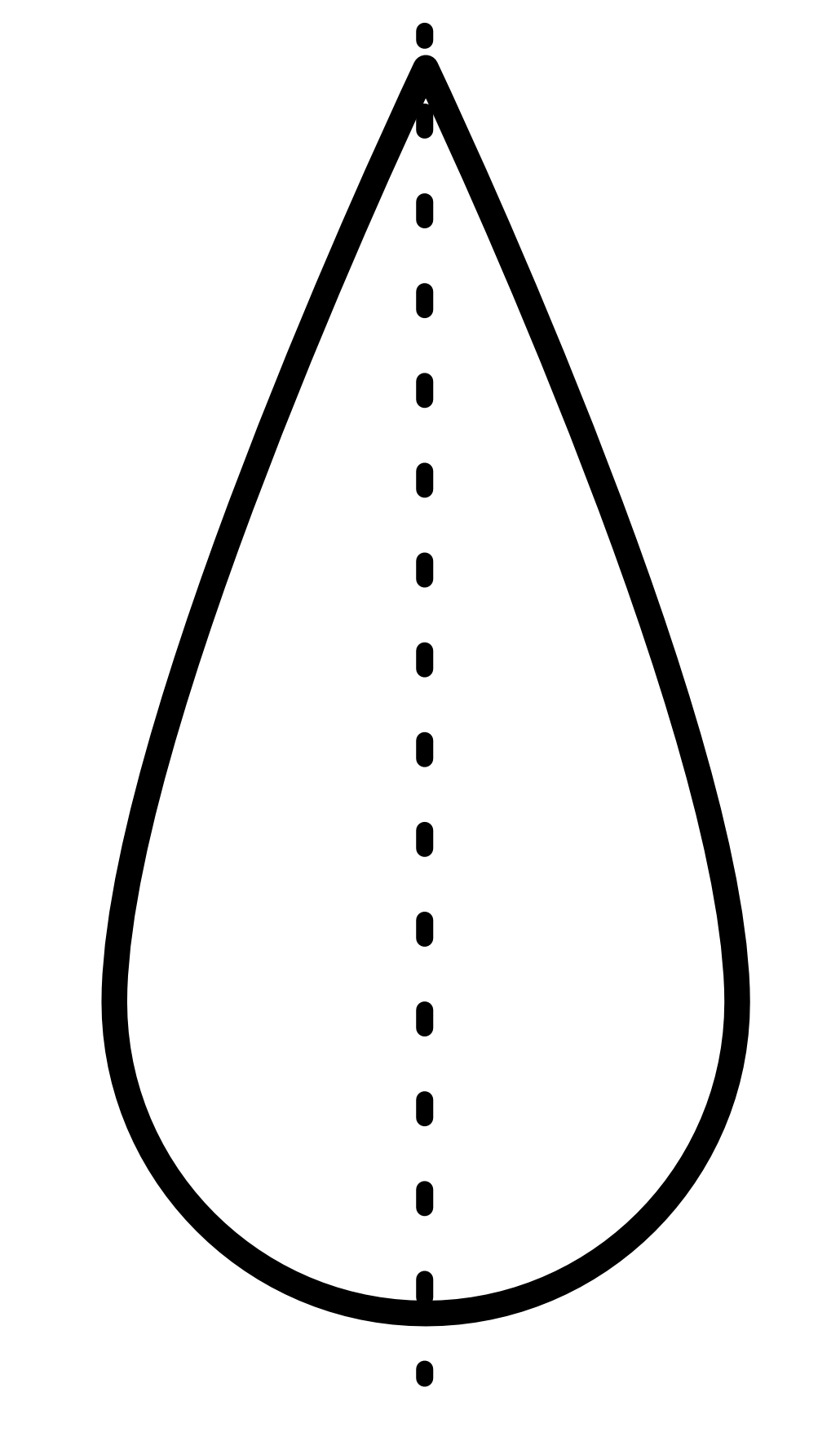

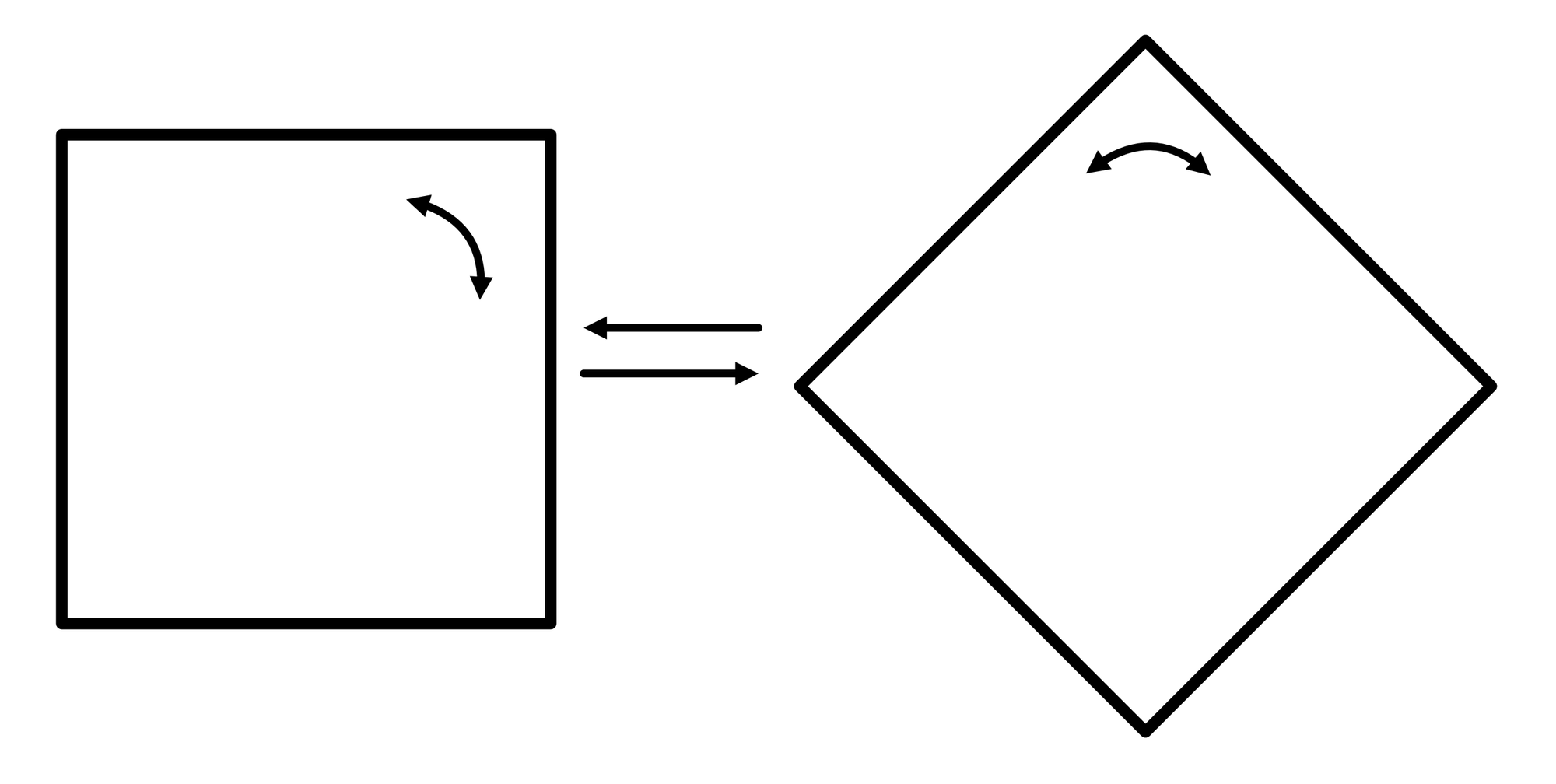
Figure 2: Upper Left- A circle is invariant to any rotation. | Upper Center- A square is invariant to 90 degree rotations. | Upper Right- Pentagons are invariant to 72 degree rotations. | Lower Left- This droplet is invariant to a flip about its horizontal center | Lower Center- Solid colors extending out to infinity are invariant to rotation and translation | Lower Right- A square is invariant to two sequential 45 degree rotations, irrespective of the order or direction they are applied.
Uniform Scalar Fields
Below is an example of a field. The axes, shown in white aren't part of the field, they are just there to help us assign spacial coordinates to parts of the field. This is called a color field because each location in 2D space is assigned a color.

The field above is an example of a uniform field. It is blue everywhere. Notably, this is also a scalar field because the property color is a directionless quantity. This kind of field is appropriately called a uniform scalar field.
Uniform fields are generally the most unremarkable. Consider an example where a blob of the field is moving to the right. This is shown below with a blob and an arrow.

Regardless of this motion, to an observer, the field is still uniformly blue and the motion cannot even be perceived. Below is an animation of the above motion.

Uniform fields are spatially symmetric. No matter how we translate or rotate our reference coordinate frame, the field looks the same! This is called translation and rotation invariance.
In the below sequence, an additional coordinate system is generated from the first through a translation and rotation. Then the camera is aligned to the new frame. The field appears identical in the new frame as it did in the old frame.

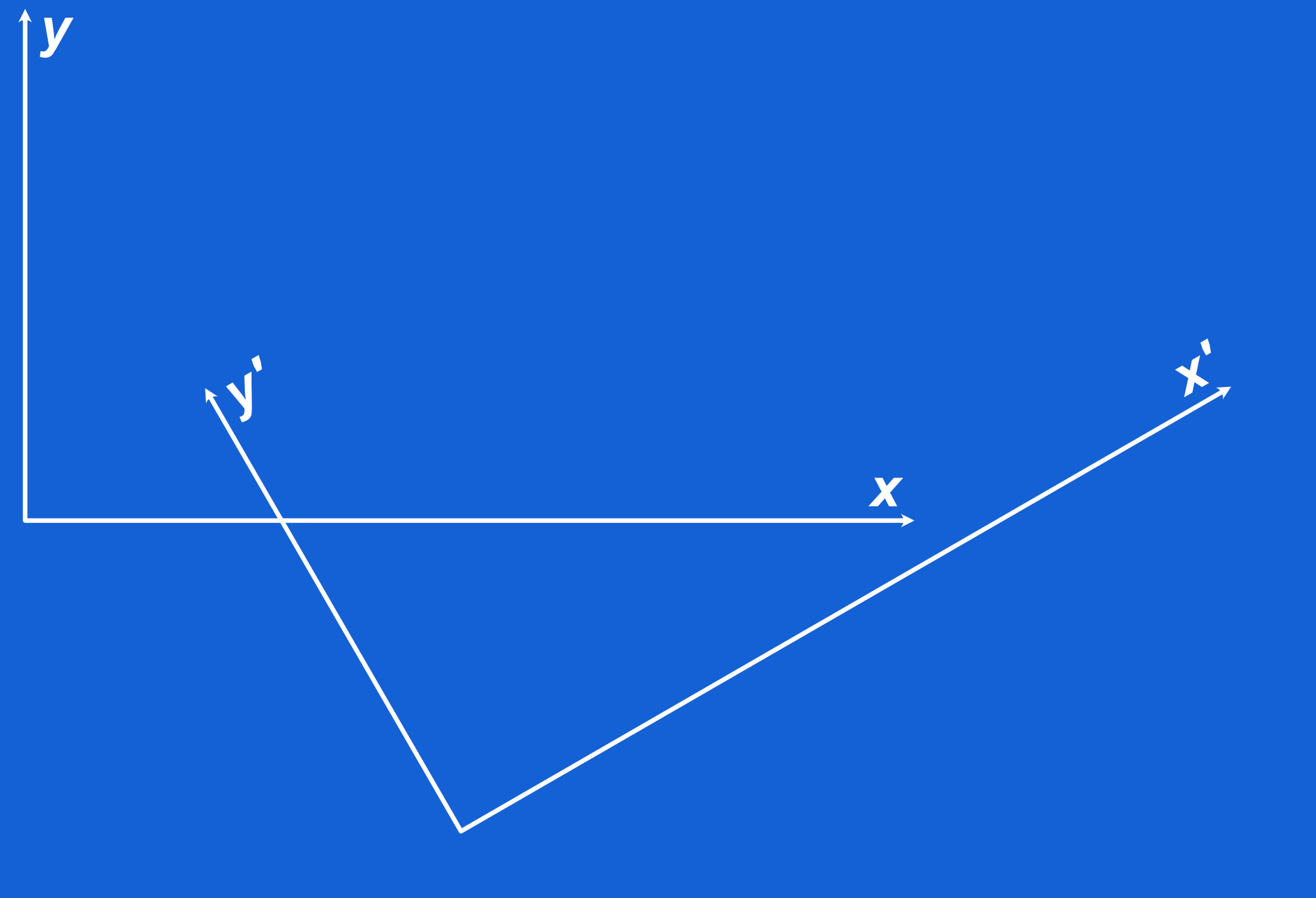

Figure 6: Left- Uniform scalar field with respect to main reference frame | Center- Main reference frame has been translated and rotated into the prime reference frame | Right- When similarly framed in the camera, the uniform scalar field in the prime reference frame appears identical to the main reference frame.
Fields are not limited to two dimensions (though 2D fields are certainly easier to represent on a flat screen). The below diagram demonstrates a 3D uniform color field. No matter what coordinate in space you measure the color at, it is the same shade of blue.

Though we had chosen color as the field property, we could have chosen anything. In the below example, we've chosen temperature (in Kelvin) as the field property and used a color scale.

Rather than using colors, it might seem reasonable to directly label the field everywhere with numbers.

This is of course chaos since we can't read most of the numbers. One solution is to sparsely label points in space so that we can read the numbers.

Though the field graph does not tell us the temperature between the labels, we can reasonably interpolate to get a close approximation. Above, we surmise that the temperature between the numbers is always 3.
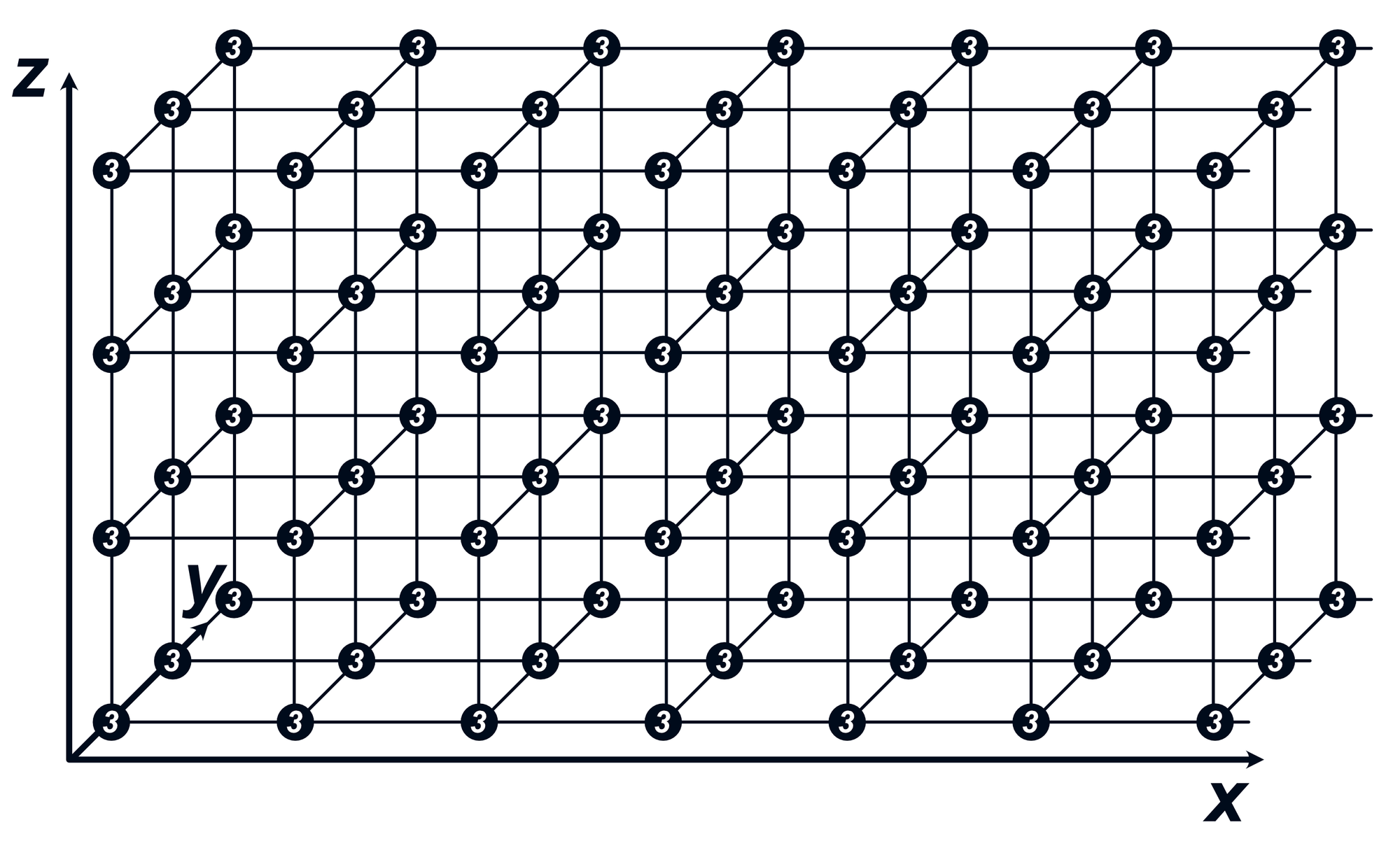
When moving to 3D space, even the sparse intervals yield a chaotic diagram.

To resolve this, we can make the points even more sparse (and add perspective grids) to make them intelligible.
Uniform Vector Fields
In the previous sections, the property being mapped to space was a scalar. A uniform vector field is just like a uniform scaler field except the property being mapped is a vector. For example, we might use a uniform vector field to describe the velocity of a fluid.
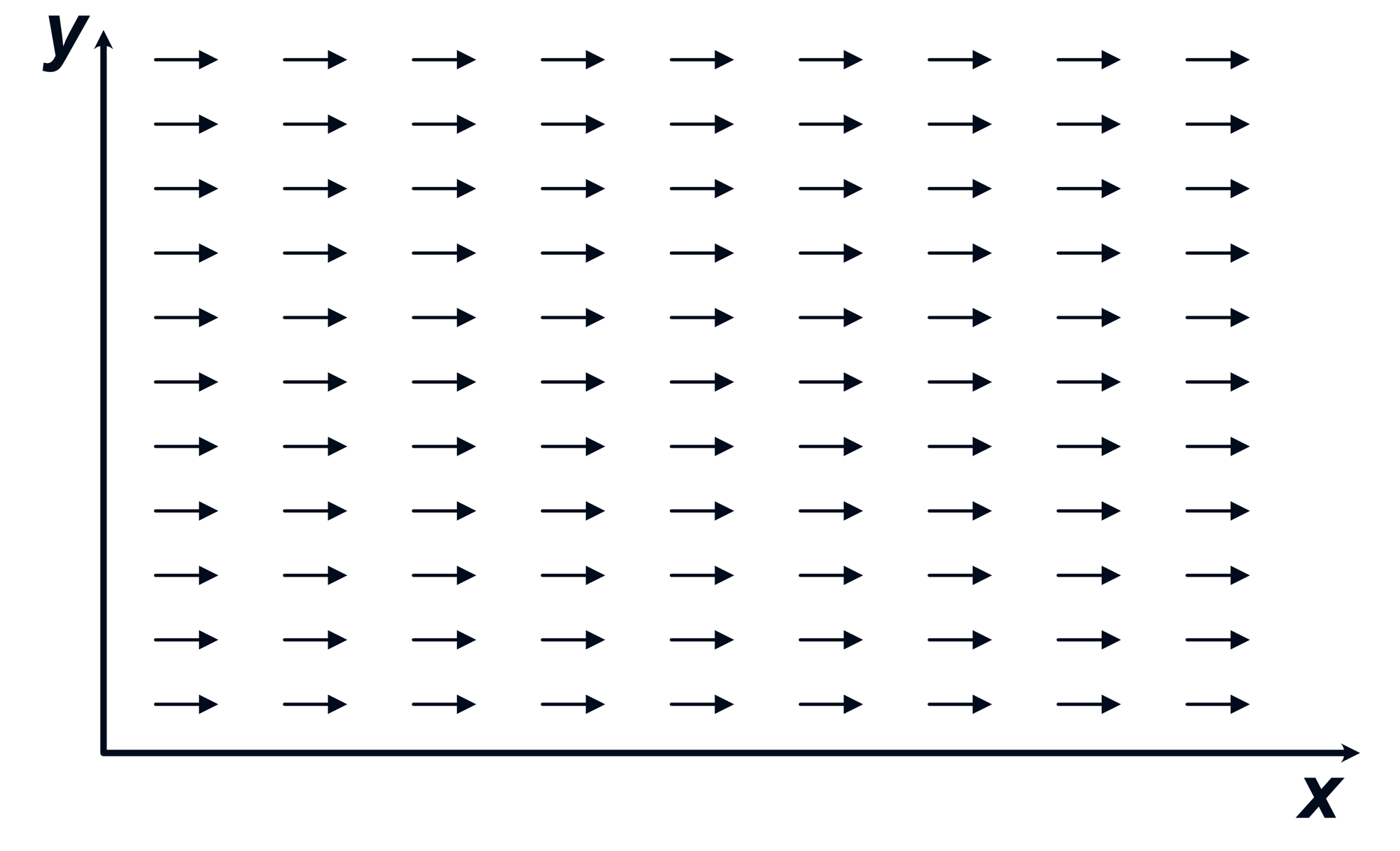
The above diagram depicts that the fluid flow is from left to right. We can use the length of the arrows to depict the magnitude of the field, though it is also valid to use colors or labels as was done in the previous sections.

Uniform vector fields are translation invariant but not rotation invariant. When the reference frame is rotated, every point in the field now points in a different direction in the new frame.
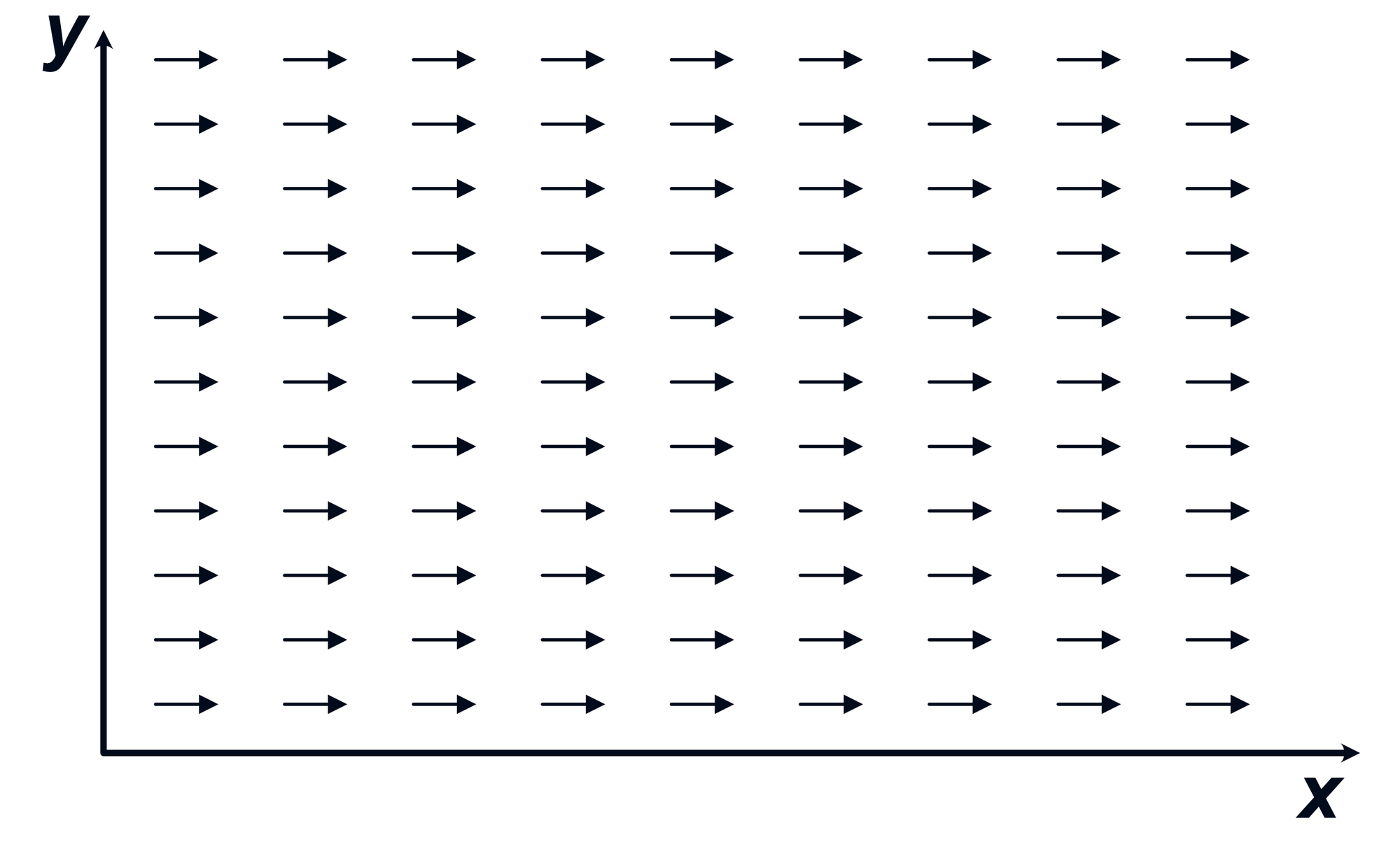
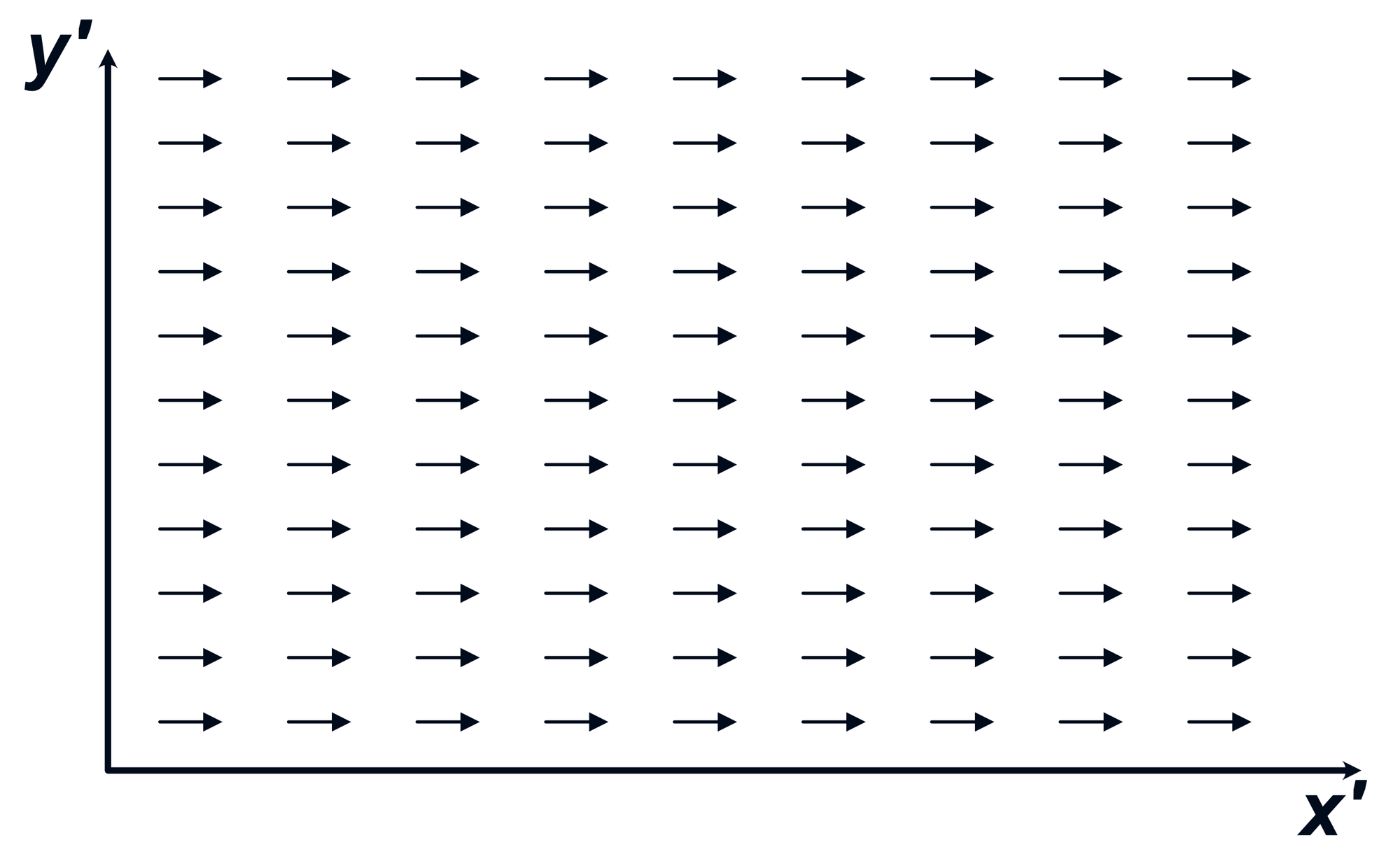

Figure 15: Left- A vector field in the main reference frame. | Center- When the main reference frame is translated into a new primed frame, the uniform vector field appears identical. | Right- When the main reference frame is rotated into a new primed frame, the uniform vector field now appears rotated.
Non-Uniform Fields
The uniform fields were useful to help us become familiar with the concept of fields but most real applications involve properties that change over space. These are called non-uniform fields. Non-uniform fields (both scalar and vector) are conceptually similar to uniform fields except that the field property is no longer the same everywhere. Below, a number of non-uniform fields are depicted.


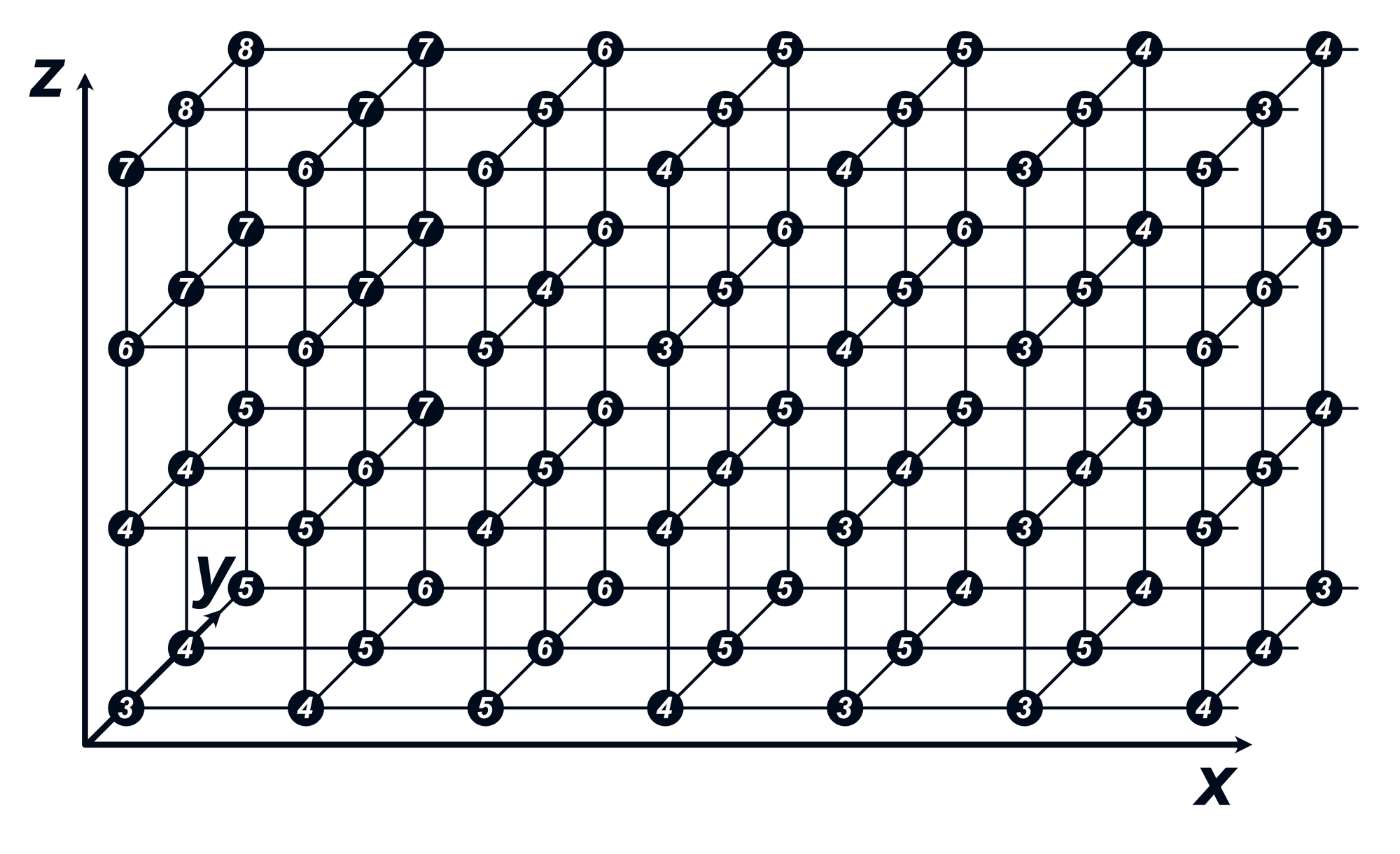
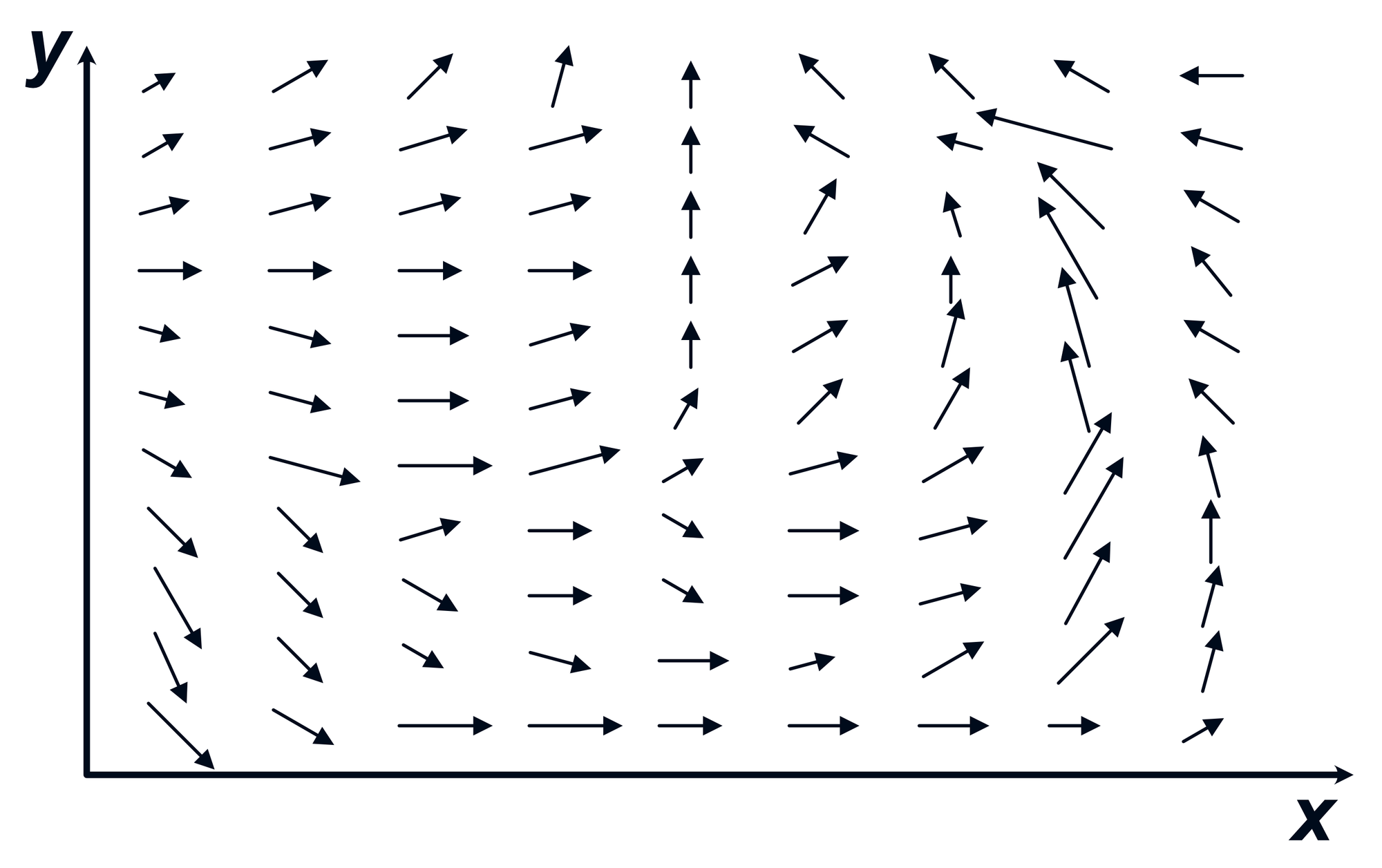
Figure 16: Upper Left- Non-uniform scalar 2D field, given by colors | Upper Right- Non-uniform scalar 2D field, given by labels| Lower Left- Non-uniform scalar 3D field, given by labels | Lower Right- Non-uniform vector 2D field
Time-Varying Fields
Up to this point, the fields we have discussed have not been changing in time. These kinds of fields are called static fields or temporally uniform fields (because they are uniform against the backdrop of flowing time). Equally valid fields are time-varying or time-dependent fields. These fields have properties that change over time. Time-varying fields can be scalar or vector fields.

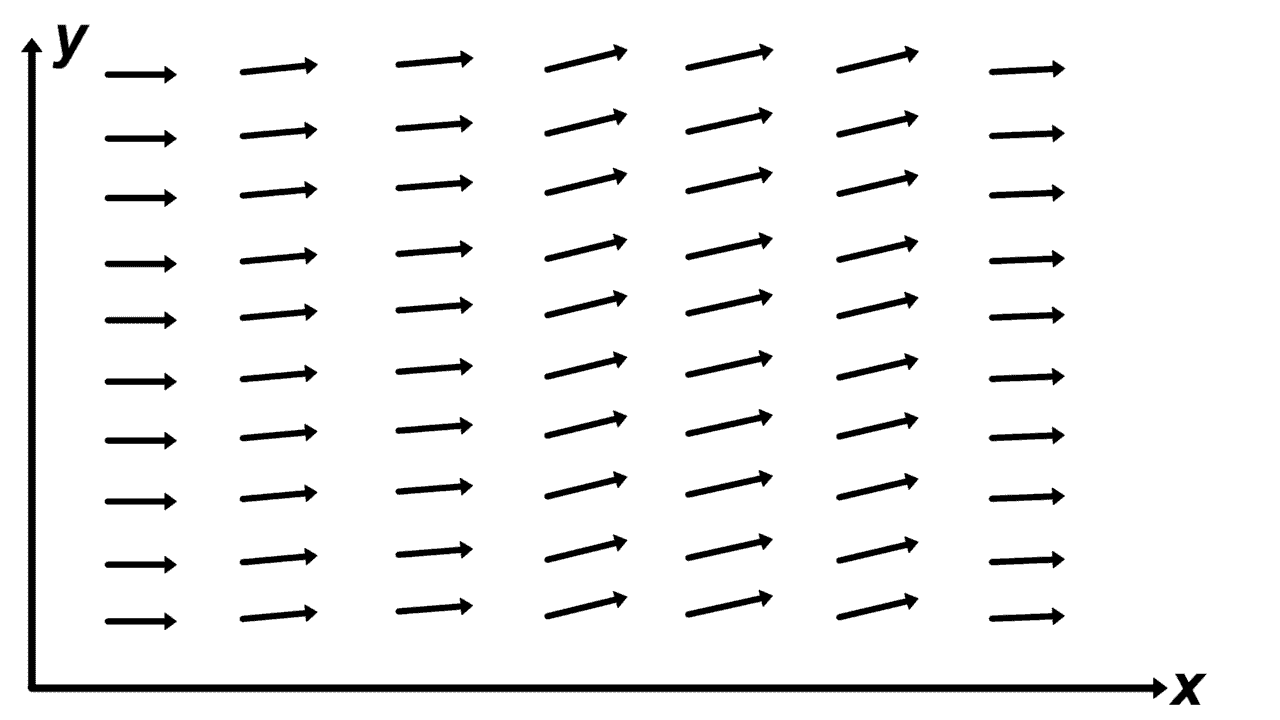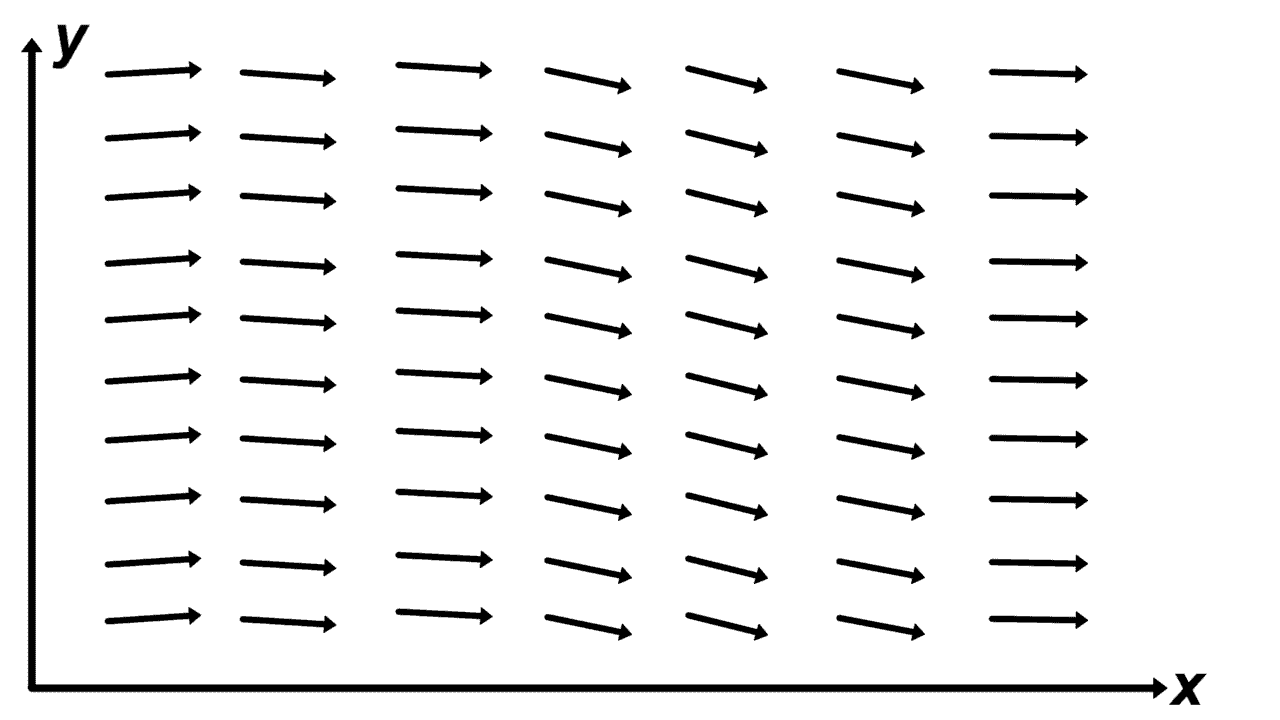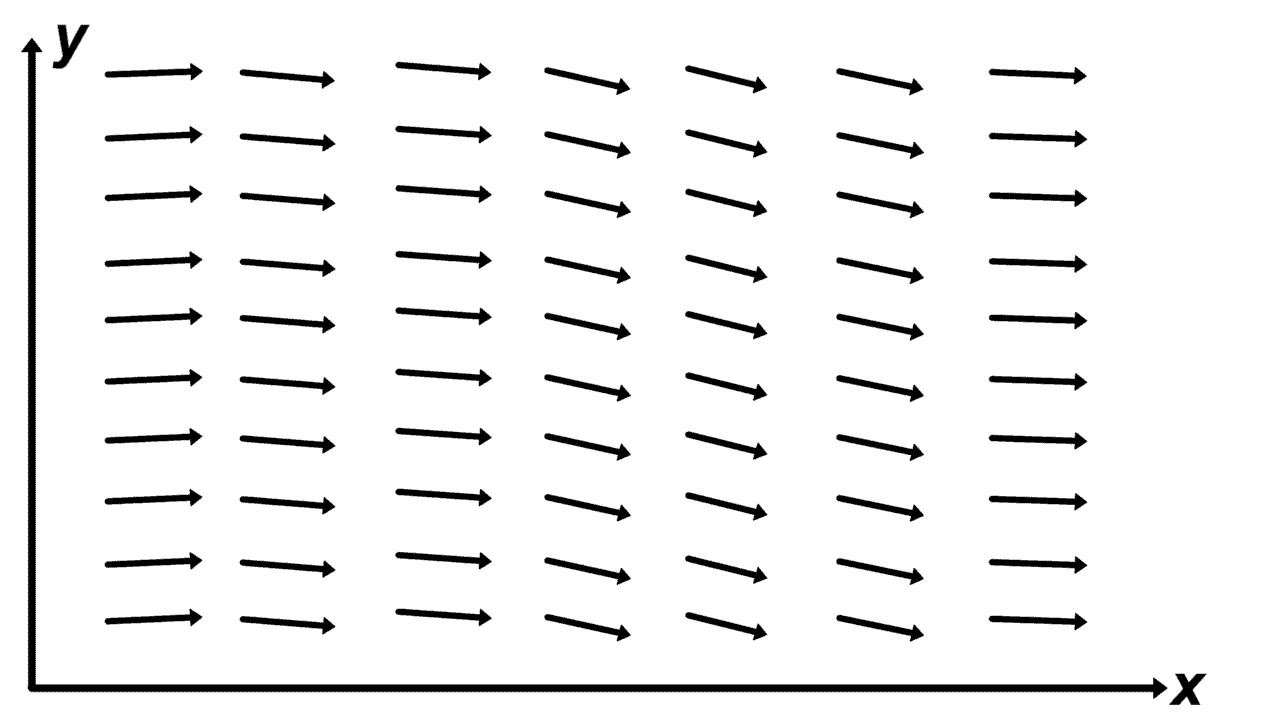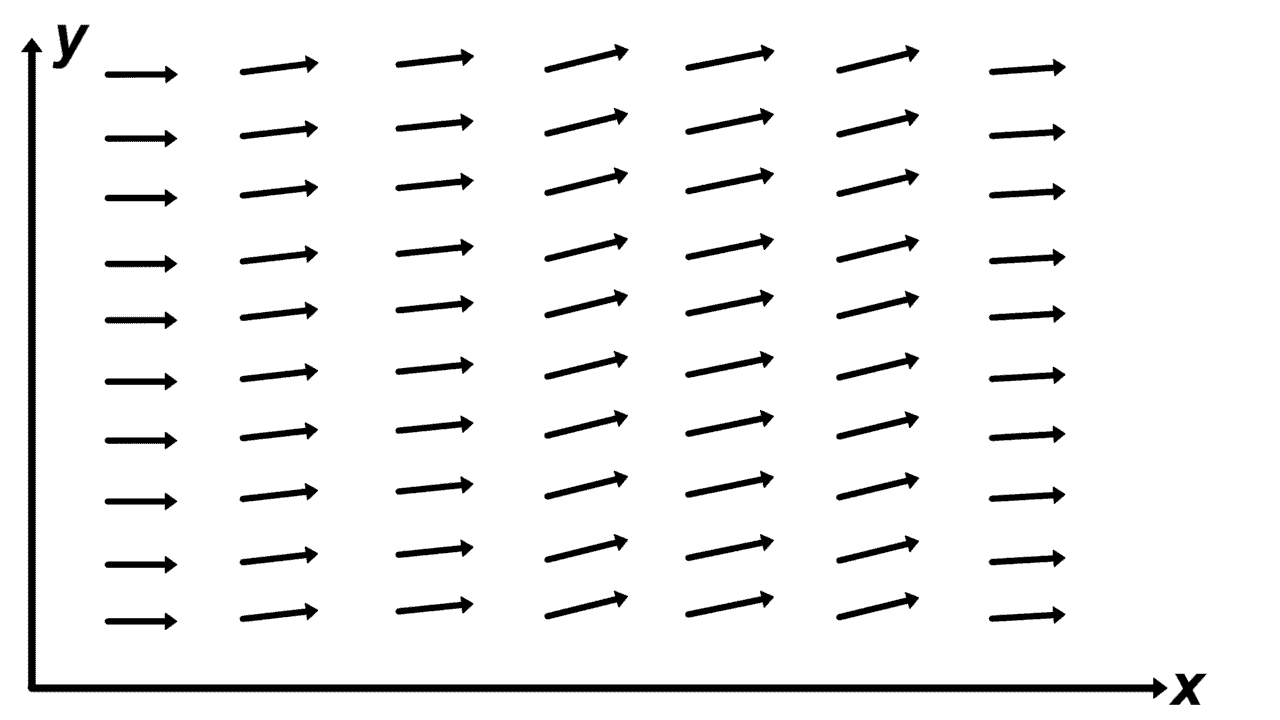
Figure 17: Left- Time-varying non-uniform scalar field | Right- Time-varying non-uniform vector field
It is possible for a field to be uniform and time-varying, which would mean that the entire field changes with time uniformly.

Field Descriptors
We have to this point discussed many different kinds of fields. The fields themselves consist of their location and time dependent field property, but as we've seen, they can be uniform or non-uniform, scalar or vector, etc. To describe the field, we can compound the field's descriptors:
uniformity type|temporal type|property type
The below are all examples of fields:
- Uniform static scalar field
- Non-uniform static scalar field
- Uniform static vector field
- Non-uniform static vector field
- Uniform time-varying scalar field
- Non-uniform time-varying scalar field
- Uniform time-varying vector field
- Non-uniform time-varying vector field
Mathematics of Fields
The mathematics of fields are actually very simple. As the degrees of symmetry go down, the complexity of the equations go up. We will assume that the spacial coordinates are the standard 3D cartesian $x$, $y$, and $z$ but the spacial coordinates could be 2D coordinates, polar, cylindrical, spherical, or any other convenient method of describing space.
Uniform Static Scalar Fields
The general form for a uniform static scalar field $F$ returns a single scalar value $u$ everywhere, where $u$ is the uniform value of the field:
$$F = u$$
Non-Uniform Static Scalar Fields
The general form for a non-uniform static scalar field $F$ is a function that accepts spacial coordinates as arguments and returns the value of the field:
$$F = f(x,y,z)$$
It could also be said that the non-uniform static scalar field $F$ is a function that accepts a position vector $\overline{p}$, corresponding to the vector between the origin and a point in space. The function returns the value of the field:
$$F = f(\overline{p})$$
Uniform Static Vector field
The general form for the uniform static vector field $\overline{F}$ returns a single vector value $\overline{u}$ everywhere, where $\overline{u}$ is the uniform vector value of the field:
$$\overline{F} = \overline{u}$$
Non-Uniform Static Vector Field
The general form for a non-uniform static vector field $\overline{F}$ is a function that accepts spacial coordinates as arguments and returns the vector value of the field:
$$\overline{F} = \overline{f}(x,y,z)$$
It could also be said that the non-uniform static vector field $\overline{F}$ is a function that accepts a position vector $\overline{p}$, corresponding to the vector between the origin and a point in space. The function returns the vector value of the field:
$$\overline{F} = \overline{f}(\overline{p})$$
Uniform Time-Varying Scalar Field
The general form for a uniform time-varying scalar field $F$ is a function $u(t)$ that accepts a time as an argument and returns a single scalar value $u$ everywhere:
$$F = u(t)$$
Non-Uniform Time-Varying Scalar Field
The general form for a non-uniform time-varying scalar field $F$ is a function that accepts spacial coordinates and time as arguments and returns the value of the field:
$$F = f(x,y,z,t)$$
It could also be said that the non-uniform time-varying scalar field $F$ is a function that accepts time and a position vector $\overline{p}$,corresponding to the vector between the origin and a point in space. The function returns the value of the field:
$$F = f(\overline{p},t)$$
Uniform Time-Varying Vector Field
The general form for the uniform time-varying vector field $\overline{F}$ is a function $\overline{u}(t)$ that accepts a time as an argument and returns a single vector value $\overline{u}$ everywhere:
$$\overline{F} = \overline{u}(t)$$
Non-Uniform Time-Varying Vector Field
The general form for a non-uniform time-varying vector field $\overline{F}$ is a function that accepts spacial coordinates and time as arguments and returns the vector value of the field:
$$\overline{F} = \overline{f}(x,y,z,t)$$
It could also be said that the non-uniform time-varying vector field $\overline{F}$ is a function that accepts a time and position vector $\overline{p}$, corresponding to the vector between the origin and a point in space. The function returns the vector value of the field:
$$\overline{F} = \overline{f}(\overline{p},t)$$
