Logarithmic Arithmetic
Required Prerequisites- Exponential Arithmetic
Today, the logarithm is taught mostly in context of subjects like compound interest, decay rates, sound pressures, and earthquake intensities. Though useful, these subjects do not give the logarithm the credit it is due. From 1624 (when Henry Briggs published Arithmetica Logarithmica) until 1972 (when Hewlett-Packard release the first scientific pocket calculator), the logarithm was the primary means by which most of the world performed arithmetic. Logarithms were used to design airplanes, create the atomic bomb, send men to the moon, and so much more. If not for the discovery of logarithms, we would not be enjoying any of the modern technological marvels we have today.
Multiplication and Division are Hard!
Subtraction and addition by hand are relatively easy, but division and multiplication are hard. Even simple calculations like $\frac{26}{7}$ or $641.85*7.31$ require an incredible amount of mental gymnastics to compute using manual methods. To make matters worse, the amount of time required for division is not fixed. The result of $\frac{26}{7}$ is irrational, with infinitely many decimals. Technically, the calculation will never be done!

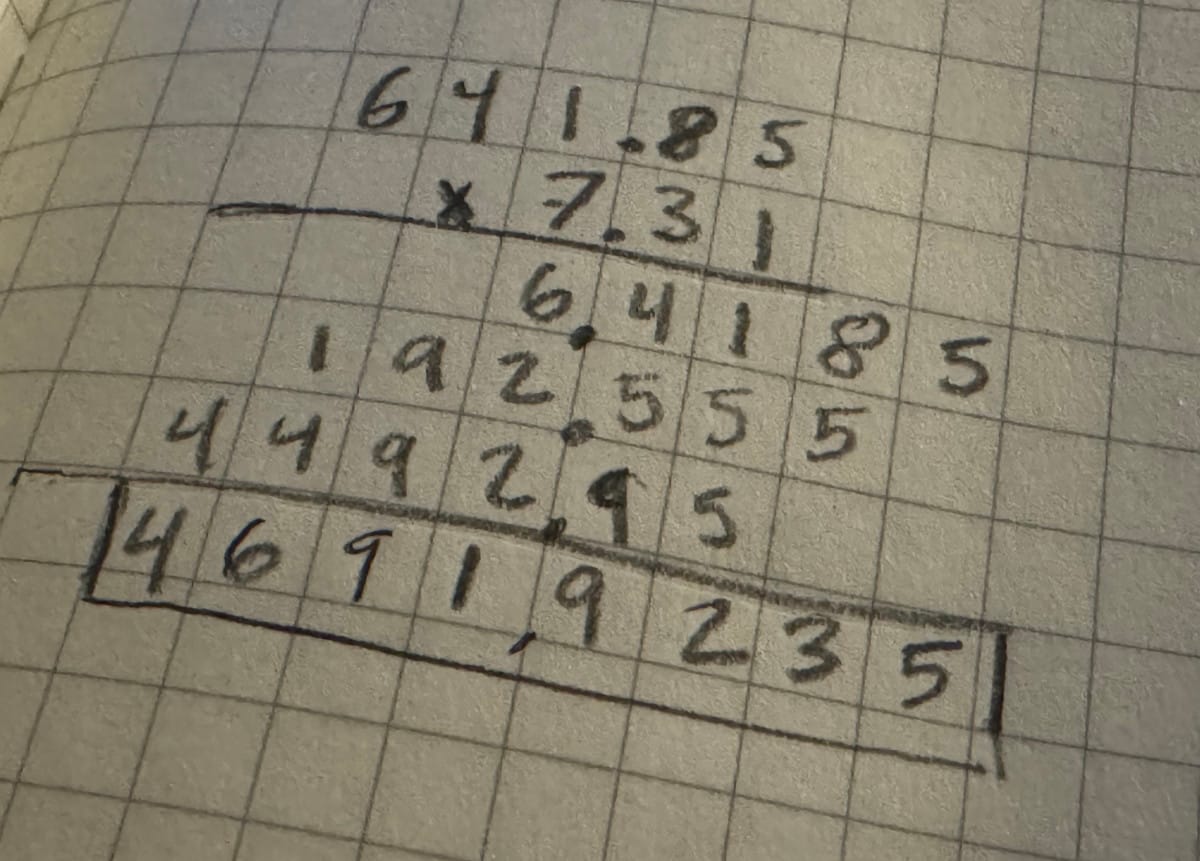
Figure 1: Left- Long division demonstrating $\frac{26}{7} = 3.71428571$ | Right- Long multiplication demonstrating $641.85*7.31 = 4691.9235$.
If only multiplication and division could be simpler... as we will see shortly, with the power of logarithms, they can be!
The Logarithm Definition
To derive the logarithm, we will be using exponential arithmetic extensively, I recommend reviewing it.
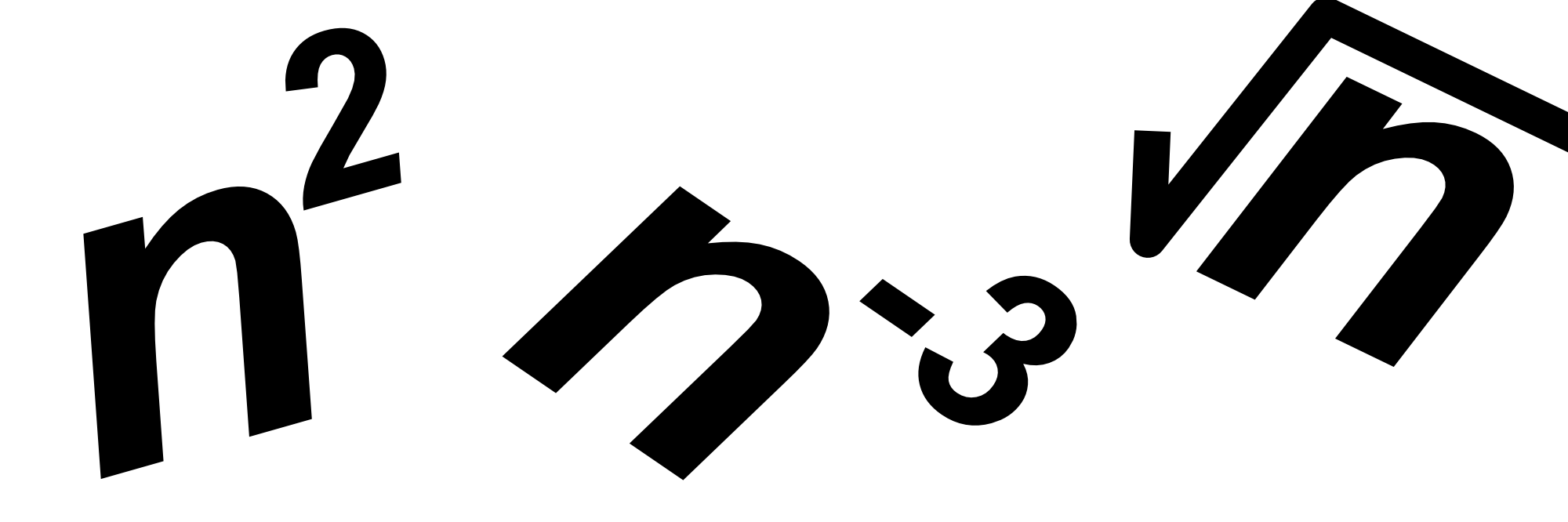
During exponentiation, we multiply a base number $b$ by itself multiple times $p$ to obtain a new number $n$:
$$n = b ^p$$
In a very simple example, $b=2$ and $p=3$ so that:
$$2 ^3 = 2 * 2 * 2 = 8$$
Consider the relationship $n = b^p$ and suppose we have the base number $b$, but instead of knowing $p$, we have the new number $n$ and need to solve for $p$. For example, let $n = 4$ and $b = 2$:
$$2 ^p = 4$$
What is the value for $p$ that makes this equation true? Obviously, $p = 2$:
$$2 ^ 2 = 4$$
Often, this isn't such an easy problem. If $n = 1.5$ and $b =3$, what is $p$?
$$3 ^{p} = 1.5$$
This problem of finding the power $p$ that makes $n = b ^p$ true is perfectly reasonable but difficult to write down nicely with our current symbols; we can't write an equation with $p$ by itself on one side.
Consider the area of a square. The area $A$ of a square with side length $L$ is given by:
$$L^2 = A$$
This equation has an input and output, each on separate sides of the equality sign:
$$(\underbrace{L}_{input})^2 = \underbrace{A}_{output}$$
The input of the equation is on the left. The output on the right. This equation is neat and concise, but in the problem of solving for the power in an exponential, it is not so easy to separate the inputs $n$, $b$, and output $p$:
$$n = b ^p$$
The base-$b$ logarithm is by definition, the mathematical operation that when performed on an exponential $b^p$, returns the power of the exponential:
$$\boxed{\text{log}_b{(b^p)} = p}$$
For example, consider the exponential $3 ^4$. Taking the base-$3$ logarithm of $3 ^4$, we obtain:
$$\text{log}_3{(3^4)} = 4$$
If we take the base-$b$ logarithm of both sides of the equation $n = b ^p$, we obtain:
$$\text{log}_b{(n)} = \text{log}_b{(b^p)}$$
From the fundamental definition, $\text{log}_b{(b^p)} = p$, which then gives:
$$\text{log}_b{(n)} = p$$
We now have an equation with the inputs $b$, $n$ on one side and the output $p$ on the other:
$$\underbrace{\text{log}_b{(n)}}_{inputs} = \underbrace{p}_{outputs}$$
Taking the base-$b$ logarithm of both sides of $n = b^p$ has transformed it!
$$\boxed{n = b ^p\ \underbrace{\rightarrow}_{\text{log}_b}\ \text{log}_b(n) = p}$$
This process, left to right, is the logarithm transformation.
Consider the situation where we take the base number $b$ and raise it to each side of the equation $\text{log}_b(n) = p$:
$$b ^{\text{log}_b(n)} = b ^p $$
Since $n = b ^p$, we can substitute $b ^p$ with $n$ to obtain:
$$\boxed{b ^ {\text{log}_b(n)} = n}$$
This equation, obtained by exponentiating $b$ to each side of $\text{log}_b(n) = p$ is the inverse logarithm:
$$\boxed{ \text{log}_b(n) = p\ \underbrace{\rightarrow}_{b\text{^}}\ n = b ^p}$$
We now have the fundamental definition for the logarithm transformation and how to reverse it:
$$\boxed{n = b ^p\ \begin{matrix} \underbrace{\rightarrow}_{\text{log}_b} \\ \text{||} \\ \underbrace{\leftarrow}_{b\text{^}}\end{matrix}\ \text{log}_b(n) = p}$$
When $b = 2$ and $n = 4$, the base-$2$ logarithm transformation gives:
$$4 = 2 ^p\ \underbrace{\rightarrow}_{\text{log}_2}\ \text{log}_2(4) = p$$
The solution for this equation is $p = 2$. Its exponential and logarithm forms are given by:
$$4 = 2 ^2\ \underbrace{\rightarrow}_{\text{log}_2}\ \text{log}_2(4) = 2$$
Our First Logarithm Table
Suppose that for the base $3$, we create an exponential table that contains the inputs $p$ and outputs $n$ for $n = 3 ^p$:
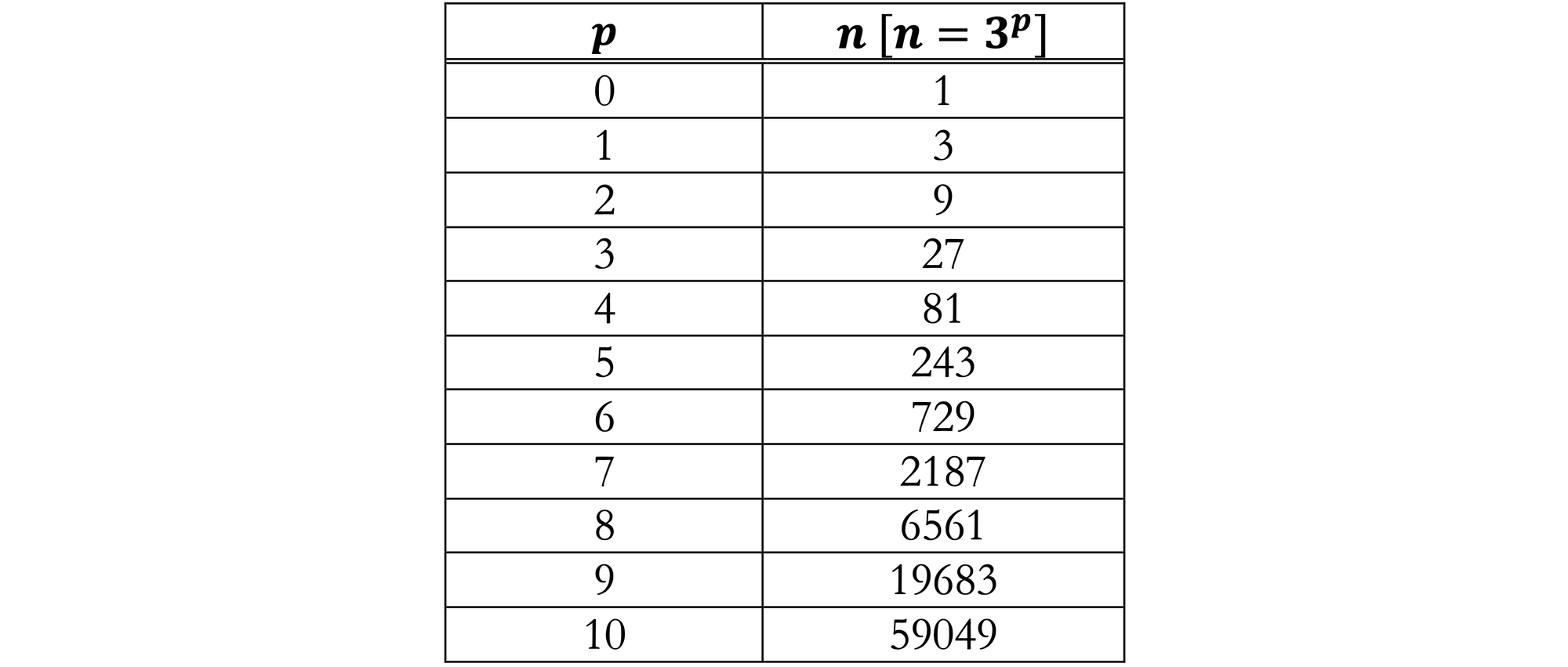
To convert the exponential table to a logarithm table, we use the logarithm transformation equation to relabel the table's columns so that $n$ is the input and $p$ is the output:
$$n = 3 ^p\ \underbrace{\rightarrow}_{\text{log}_3}\ \text{log}_3(n) = p$$
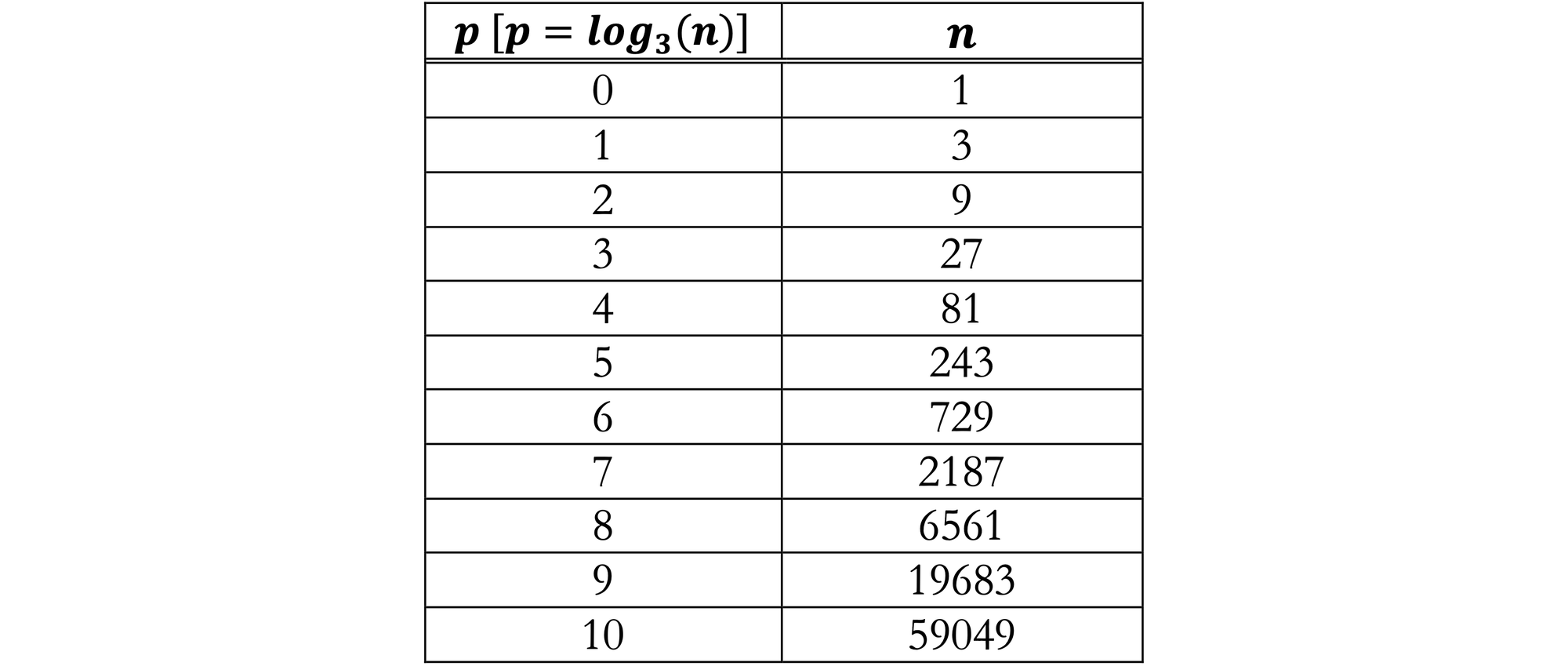
Since the contents of the exponential and logarithmic tables are identical, proper labeling of the columns permit the same table to be used for both. The table is most useful for us with $n$ on the left.
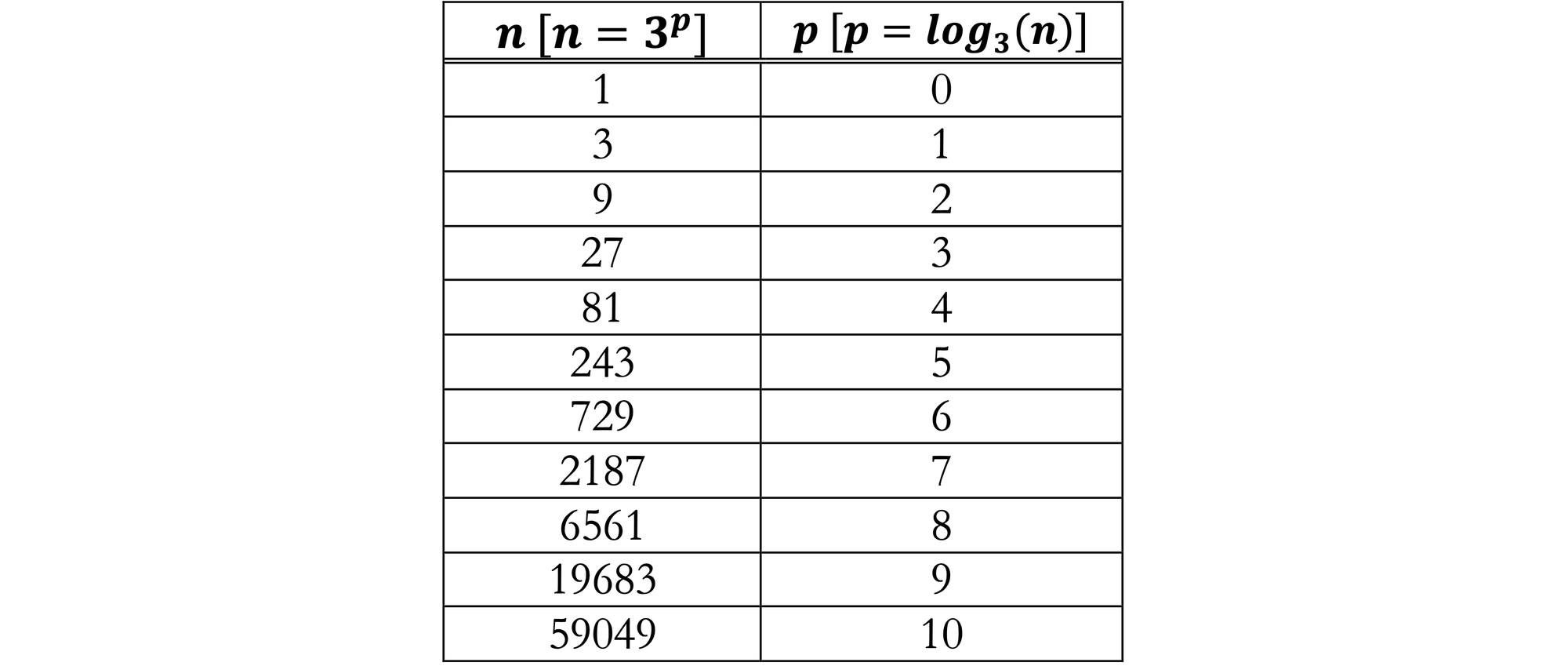
Each row in the $p$ column is the base-$3$ logarithm of the $n$ column, $\text{log}_3(n)$ Each row of the $n$ column is $3$ raised to the power $p$ column, $b ^p$.
Using the base-$3$ table, $\text{log}_3(243) = 5$, $\text{log}_3(27) = 3$, and $3 ^6 = 729$.
Easy Multiplication using Logarithms
Using logarithms, we can multiply two exponential numbers $n_1$ and $n_2$ with shared base $b$:
$$n_1 = b ^{p_1},\ n_2 = b ^{p_2}$$
Taking the base-$b$ logarithm of each side of these equations, we obtain:
$$\text{log}_b(n _1) = p _1, \ \text{log}_b(n _2) = p _2$$
If we multiply together $n_1$ and $n_2$ and use the product of exponentials rule we obtain:
$$n_1 * n_2 = b ^{p_1} * b ^{p_2} = b ^{p_1 + p_2}$$
Using the logarithm definition, the base-$b$ logarithm of both sides of this equation is:
$$\text{log}_b(n _1 * n _2) = \text{log}_b(b ^{p_1 + p_2}) = p_1 + p_2$$
Since $\text{log}_b(n _1) = p _1$ and $\text{log}_b(n _2) = p _2$, we substitute to obtain:
$$\boxed{\text{log}_b(n _1 * n _2) = \text{log}_b(n _1) + \text{log}_b(n _2)}$$
This fundamental logarithm property is called the product rule.
A practical use of this property can be demonstrated with an example. We desire to calculate $9 * 243$. From the base-$3$ table, we observe that:
$$\text{log}_3(9) = 2,\ \text{log}_3(243) = 5$$
Using the product rule property, we find:
$$\text{log}_3(9 * 243) = \text{log}_3(9) + \text{log}_3(243) = 2 + 5 = 7$$
$$\text{log}_3(9 * 243) = 7$$
Now, the base $3$ can be exponentiated to the power of each side:
$$3 ^{\text{log}_3(9 * 243)} = 9 * 243 = 3 ^7$$
Using the base-$3$ table, $3 ^7 = 2187$. Therefore:
$$9 * 243 = 2187$$
The problem of performing multiplication has been reduced to using a table and addition!
Easy Division using Logarithms
Using logarithms, we can divide two exponential numbers $n_1$ and $n_2$ with shared base $b$:
$$n_1 = b ^{p_1},\ n_2 = b ^{p_2}$$
Taking the base-$b$ logarithm of each side of these equations, we obtain:
$$\text{log}_b(n _1) = p _1, \ \text{log}_b(n _2) = p _2$$
When dividing $n_1$ by $n_2$, we obtain:
$$\frac{n_1}{n_2} = n_1 * n_2 ^ {-1} = b ^{p_1} * b ^{-p_2} = b ^{p_1 - p_2}$$
Using the logarithm definition, the base-$b$ logarithm of both sides of this equation is:
$$\text{log}_b(\frac{n _1}{n _2}) = \text{log}_b(b ^{p_1 - p_2}) = p_1 - p_2$$
Since $\text{log}_b(n _1) = p _1$ and $\text{log}_b(n _2) = p _2$, we substitute to obtain:
$$\boxed{\text{log}_b(\frac{n _1}{n _2}) = \text{log}_b(n _1) - \text{log}_b(n _2)}$$
This fundamental logarithm property is called the quotient rule.
A practical use of this property can be demonstrated with an example. We desire to calculate $\frac{729}{9}$. From the base-$3$ table, we observe that:
$$\text{log}_3(729) = 6,\ \text{log}_3(9) = 2$$
Using the quotient rule property, we find:
$$\text{log}_3(\frac{729}{9}) = \text{log}_3(729) - \text{log}_3(9) = 6 - 2 = 4$$
$$\text{log}_3(\frac{729}{9}) = 4$$
Now, the base $3$ can be exponentiated to the power of each side:
$$3 ^{\text{log}_3(\frac{729}{9}} = \frac{729}{9} = 3 ^4$$
Using the base-$3$ table, $3 ^4 = 81$. Therefore:
$$\frac{729}{9} = 81$$
The problem of performing division has been reduced to using a table and subtraction!
Easy Exponentiation and Roots Using Logarithms
Recall the logarithm transformation:
$$n = b ^p\ \underbrace{\rightarrow}_{\text{log}_b}\ \text{log}_b(n) = p$$
Raising both sides of $n = b ^p$ to a power $q$, we obtain:
$$n ^q = (b ^p) ^q$$
Using the power of power rule, we obtain:
$$n ^q = b ^{pq}$$
Taking the base-$b$ logarithm of both sides, we obtain:
$$\text{log}_b(n ^q) = \text{log}_b(b ^{pq})$$
$$\text{log}_b(n ^q) = pq\ \textbf{ [1]}$$
Multiplying both sides of $\text{log}_b(n) = p$ by $q$, we obtain:
$$q\text{log}_b(n) = pq\ \textbf{[2]}$$
Since $pq = pq$, statements $[1]$ and $[2]$ are equal, and we obtain:
$$\boxed{\text{log}_b(n ^q) = q\text{log}_b(n)}$$
This fundamental logarithm property is called the power rule.
A practical use of this property can be demonstrated with an example. We desire to calculate $729 ^{\frac{1}{3}}$. Using the power rule:
$$\text{log}_3(729 ^{\frac{1}{3}}) = \frac{1}{3}\text{log}_3(729)$$
From the base-$3$ table:
$$\text{log}_3(729) = 6$$
Therefore:
$$\frac{1}{3}\text{log}_3(729) = \frac{1}{3}(6) = 2$$
Exponentiating $3$ to both sides:
$$3 ^{\text{log}_3(729 ^{\frac{1}{3}})} = 729 ^{\frac{1}{3}} = 3 ^ 2$$
Using the base-$3$ table, $3 ^2 = 9$:
$$729 ^{\frac{1}{3}} = 9$$
Incredibly, the problem of finding a cubed root has been reduced to using a table and division!
Logarithms of Negative Numbers
Suppose we have a base number $b = 2$, raised to a power $p$, set equal to a new number $n = -4$:
$$2 ^p = -4$$
Unfortunately, this equation has no solution. This means that the logarithm $\text{log}_2(-4)$ also has no real solution. Accordingly, the base-$b$ logarithm for any negative number $-n$ is undefined.
$$\text{log}_b(-n) = undefined$$
Though the logarithm of a negative number is undefined, the inverse logarithm remains valid when applied to the logarithm of a negative number:
$$b ^{\text{log}_b(-n)} = -n$$
This fundamental logarithm property is called the round-trip rule.
The round-trip rule states that as long as we don't try to calculate the value of the logarithm of a negative number, negative numbers can still be taken "round-trip" through the logarithm transformation:
$$-n\ \underbrace{\rightarrow}_{\text{log}_b}\ \text{log}_b(-n)\ \underbrace{\rightarrow}_{b\text{^}}\ b ^{\text{log}_b(-n)} = -n$$
As an example, we can take the number $-4$ round-trip through the base-$2$ logarithm transformation:
$$-4\ \underbrace{\rightarrow}_{\text{log}_2}\ \text{log}_2(-4)\ \underbrace{\rightarrow}_{2\text{^}}\ 2 ^{\text{log}_2(-4)} = -4$$
Any negative number $-n$ is equal to $-1$ times $n$:
$$-n = -1 * n$$
Taking the base-$b$ logarithm of the right side and using the product rule:
$$\text{log}_b(-1 * n) = \text{log}_b(-1) + \text{log}_b(n)$$
Exponentiating the base $b$ to both sides, we obtain:
$$b ^{\text{log}_b(-1 * n)} = b ^{\text{log}_b(-1) + \text{log}_b(n)}$$
Exponentiation rules permit the exponent to be split:
$$b ^{\text{log}_b(-1 * n)} = (b ^{\text{log}_b(-1)} ) (b ^{\text{log}_b(n)})$$
Simplifying, we obtain:
$$-1 * n = -1 *n$$
As has been shown, both $-1$ and $-n$ make it round-trip though the logarithm transformation unmodified. Consider when a negative number $-n$ is multiplied by another number $m$:
$$-n * m = -1 * n * m$$
Taking the logarithm of both sides:
$$\text{log}_b(-n * m) = \text{log}_b(-1) + \text{log}_b(n) + \text{log}_b(m)$$
Exponentiating the base $b$ to both sides, we obtain:
$$b ^{\text{log}_b(-n * m)} = b ^{\text{log}_b(-1) + \text{log}_b(n) + \text{log}_b(m)}$$
$$b ^{\text{log}_b(-n * m)} = (b ^{\text{log}_b(-1)}) (b ^{\text{log}_b(-1) + \text{log}_b(n) + \text{log}_b(m)})$$
Simplifying, we obtain:
$$-n * m = b ^{\text{log}_b(-1) + \text{log}_b(n) + \text{log}_b(m)}$$
$$-n * m = (b ^{\text{log}_b(-1) })(b ^{\text{log}_b(n)})(b ^{\text{log}_b(m)})$$
$$-n * m = -1 * n * m$$
When performing multiplication or division, negative signs are preserved and can be propagated without needing to track the negative sign through the round-trip process.
We can also use logarithms to calculate the value of exponentiated negative numbers, though we've not yet arrived at a point where doing so is very useful. First, the negative number should be separated into positive and base-$(-1)$ exponentiated numbers:
$$\sqrt{-5} = \sqrt{5} * \sqrt{-1}$$
After separation, the positive root can be calculated as normal using logarithm rules and tables, $\sqrt{5} = 2.236$. Substituting:
$$\sqrt{-5} = \sqrt{5} * \sqrt{-1} = 2.236 * \sqrt{-1}$$
$\sqrt{-1}$ is a complex number, which we explored briefly in the article on quadratic functions.
A Clarification on the Existence of Logarithms for Negative Numbers
This is an advanced note. Unless you are a devout mathematics enthusiast, you can likely ignore this clarification.
To say that the logarithm of a negative number is undefined is not entirely correct. If the result of the logarithm is required to be a real number, then the logarithm of a negative number is indeed undefined. However, if we permit the result of a logarithm to be a complex number, then the logarithm of a negative number does exist.
Though the logarithm of a negative number technically does exist, the round-trip rule means it's not typically needed for conventional arithmetic. Because calculating logarithms of negative numbers is a more complex topic, it will be left for a future discussion.
The Base-10 Logarithm Table
Earlier, we created and used a base-3 logarithm table for a number of examples, but there isn't really anything special about the base-3 logarithm. As we will see shortly, the base-10 logarithm actually has a property that makes it excellent for arithmetic. Below is a simple base-$10$ table:
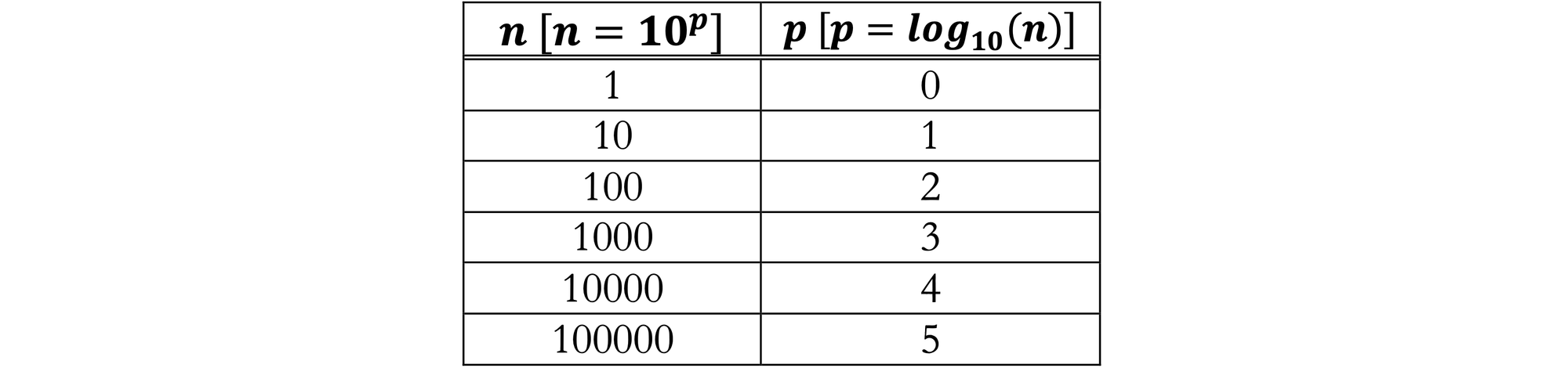
Consider we want to multiply two numbers, $6432.34$ and $56.712$. We just need a table with $\text{log}_{10}(6432.34)$ and $\text{log}_{10}(56.712)$... except our table sucks. We clearly need a bigger one!
While calculating the base-$10$ logarithms of powers of $10$ is easy, doing so for arbitrary numbers is very difficult. Even calculating $\text{log}_{10}(2)$ is an exhaustive exercise. To most people, calculating a giant table of logarithms would seem like an insane task, but English mathematician Henry Briggs saw this challenge as an opportunity to change the world. Briggs, assisted by a group of human computers, published base-$10$ logarithm tables for the integers $1-20,000$ and $90,000-100,000$ in Arithmetica Logarithmica in 1624.


Figure 2: Example pages from Henry Briggs' Arithmetica Logarithmica, 1624
The work was grueling, but the result was worth it. Briggs' initiated an acceleration in mathematics that today has gifted us with technology beyond his wildest imaginations.
If you'd like to download a PDF version of Arithmetic Logarithmica, the link is available below, source scans courtesy of https://archive.org/.
Scientific Notation
The aforementioned beneficial property of the base-$10$ logarithm is that it works very well with numbers in integer scientific notation. Integer scientific notation is when a number $n$ is expressed as an integer $m$ (without any trailing zeros) multiplied by $10$ to a power $p$:
$$n = m * 10^p$$
Below are some examples of decimal numbers expressed in integer scientific notation:
$$7823.2938 = 78232938 * 10 ^{-4}$$
$$0.8293 = 8293 * 10 ^{-4}$$
$$1,838,270,000,000 = 183827 * 10^7$$
By converting a decimal number to integer scientific notation format, a logarithm table only needs to contain the logarithm value for integers.
Example of Multiplication with Base-10 Logarithm Table
We want to multiply two numbers, $6432.34$ and $56.712$. We begin by converting them to four digit scientific notation:
$$6432.34 \approx 6432 * 10 ^ 0 \: \text{and} \: 56.712 \approx 5671 * 10 ^ {-2}$$
Multiplying them together in scientific notation, we obtain:
$$(6432 * 10 ^ {0}) * (5671 * 10 ^ {-2}) = 6432 * 5671 * 10 ^ {-2}$$
Using the logarithm product rule:
$$\text{log}_{10}(6432 * 5671 * 10 ^{-2}) = \text{log}_{10}(6432) + \text{log}_{10}(5671) + \text{log}_{10}(10 ^{-2})$$
$$\text{log}_{10}(6432 * 5671 * 10 ^{-2}) = \text{log}_{10}(6432) + \text{log}_{10}(5671) - 2$$


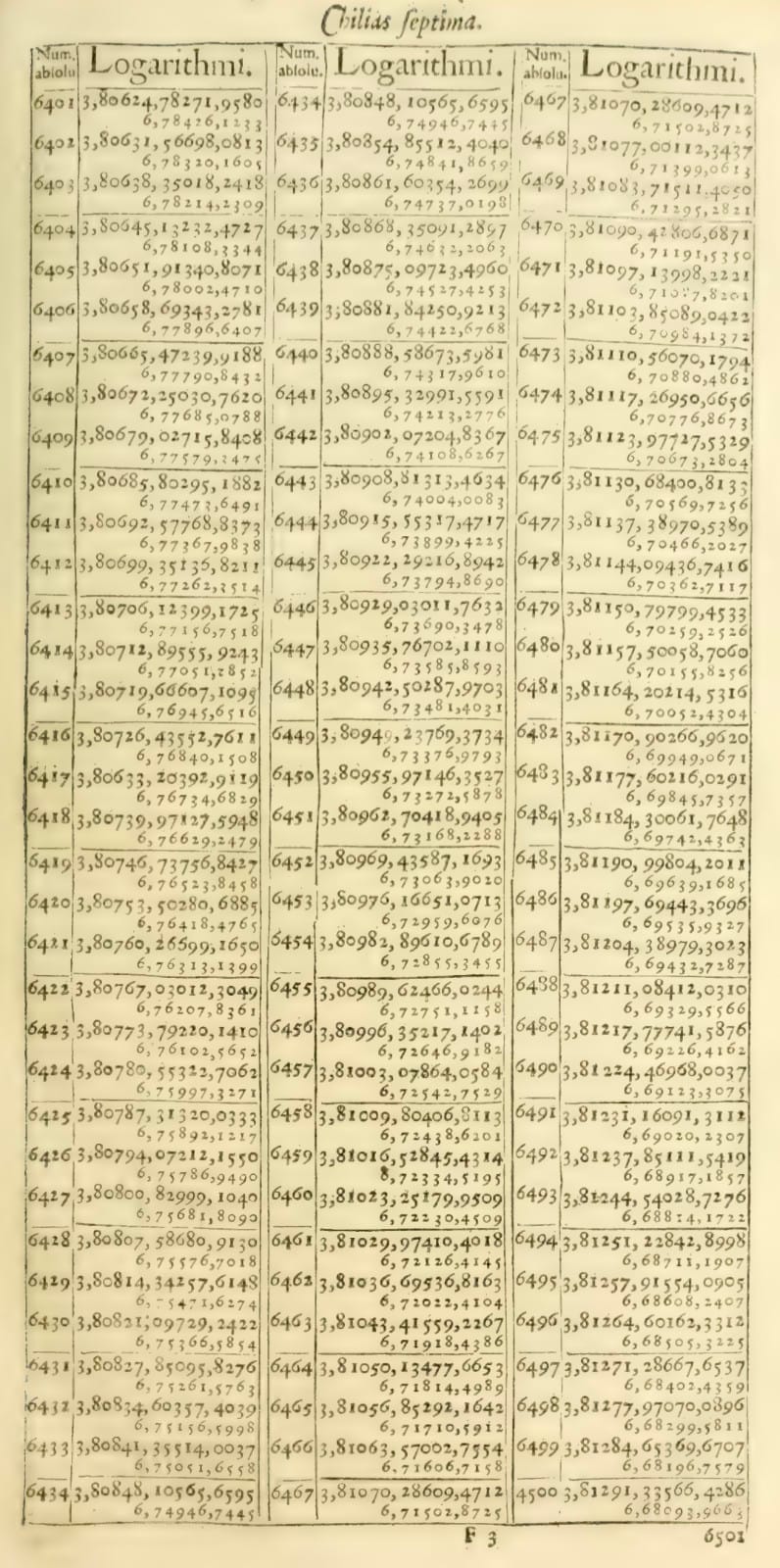
Figure 3: Pages from Arithmetica Logarithmica for calculating $6432.34*56.712$
Using Briggs' logarithm table (figure 3):
$$\text{log}_{10}(6432) = 3.80834$$
$$\text{log}_{10}(5671) = 3.75365$$
$$\text{log}_{10}(6432) + \text{log}_{10}(5671) - 2 =3.80834 +3.75365 -2 = 5.56199$$
$$\text{log}_{10}(6432 * 56.71) = 5.56199$$
Raising $10$ to each side, we obtain:
$$10 ^{\text{log}_{10}(6432 * 56.71)} = 10 ^ {5.56199}$$
$$6432 * 56.71= 10 ^ {5.56199}$$
When calculating exponentials, Briggs' table provides the most digits of precision for exponentials between $3$ and $4$ (and all exponentials need to be less than $4$). We need to reduce the non-integer exponent by multiplying by a base-$10$ exponential pair:
$$6432 * 56.71= 10 ^ {5.56199} * 10 ^{-2} * 10 ^ 2$$
$$6432 * 56.71 = 10 ^ {3.56199} * 10 ^2$$
Using the base-$10$ table (figure 3):
$$10 ^ {3.56199} = 3648$$
Therefore:
$$3648 * 10 ^2 = 364800$$
$$\boxed{6432.34 * 56.712 = 364800}$$
Note that the actual full and correct answer is $6432.34 * 56.712 = 364790.866$
Even with all of our rounding, our calculation (which we calculated using only a large table and a single addition) had an error of $<0.003\%$. Incredible.
Example of Division with Base-10 Logarithm Table
Now consider the case where we desire to divide $56.712$ by $2.31$. We begin by converting them to four digit scientific notation:
$$56.712 \approx 5671 * 10 ^ {-2} \: \text{and} \: 2.31 = 231 * 10 ^ {-2}$$
Taking their quotient, we obtain:
$$\frac{5671 * 10 ^ {-2}}{231 * 10 ^ {-2}} = \frac{5671}{231}$$
Using the logarithm quotient rule:
$$\text{log}_{10}(\frac{5671}{231}) = \text{log}_{10}(5671) - \text{log}_{10}(231)$$



Figure 4: Pages from Arithmetica Logarithmica for calculating $\frac{56.712}{2.31}$
Using Briggs' logarithm table (figure 4):
$$\text{log}_{10}(5671) = 3.75365$$
$$\text{log}_{10}(231) = 2.36361$$
$$\text{log}_{10}(5671) - \text{log}_{10}(231) = 3.75365 - 2.36361 = 1.39004$$
$$\text{log}_{10}(\frac{5671}{231}) = 1.39004$$
Raising $10$ to each side, we obtain:
$$10 ^{\text{log}_{10}(\frac{5671}{231})} = 10 ^{1.39004}$$
$$\frac{5671}{231} = 10 ^{1.39004}$$
When calculating exponentials, Briggs' table provides the most digits of precision for exponentials between $3$ and $4$ (and all exponentials need to be less than $4$). We need to increase the non-integer exponent by multiplying by a base-$10$ exponential pair:
$$\frac{5671}{231} = 10 ^{1.39004} * 10 ^{2} * 10 ^ {-2}$$
$$\frac{5671}{231} = 10 ^{3.39004} * 10 ^ {-2}$$
Using the base-$10$ table (figure 4):
$$10 ^{3.39004}= 2455$$
Therefore:
$$\frac{5671}{231} = 2455 * 10 ^ {-2} = 24.55$$
$$\boxed{\frac{56.712}{2.31} = 24.55}$$
Note that the actual full and correct answer is $$\frac{56.712}{2.31} = 24.55064935$$
Even with all of our rounding, our calculation (which we calculated using only a large table and a single subtraction) has an error of $<0.003\%$. Pretty good.

