Trigonometric Functions

Prerequisites Required- Quadratic Functions
Previously, we discussed linear and quadratic functions. Amongst the landscape of mathematical functions, trigonometric functions are some of the most important, having critical applications in geometry, physics, and engineering. To be honest, the study of triangles to such an intense degree seemed absurd to me until later when I realized that trigonometric functions are used everywhere!
Angles
Angle is the amount of rotation between the two lines; the amount one line would have to rotate to be aligned in the same direction as the other.
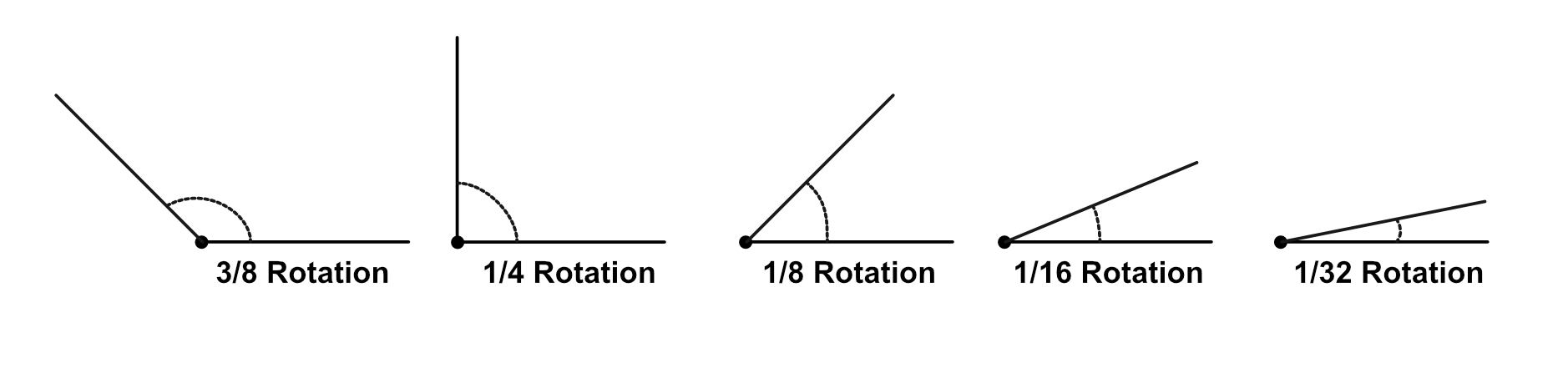
We don't normally represent angle in units of rotation but instead in units of degrees or radians. Angles in degrees are often notated with a small circle, $120$ degrees is written $120^\circ$.
Rotations to Degrees: $\theta (degrees) = \theta (rotations) *360$
$360$ degrees being equal to $1$ rotation is mostly historical baggage from ancient Babylonian astronomy and Greek geometry. However, it's very pervasive.
As an alternative to rotations or degrees, we can instead measure an angle based on the length of the radius $1$ arc that subtends it, with units of radians. The circumference of a circle of radius $1$ is $2\pi$ which is equal to $6.2831853072...$. The nature of $\pi$ is described in more detail in the below article.
Consider the below triangle/arc that is $\frac{1}{32}$ of a rotation.
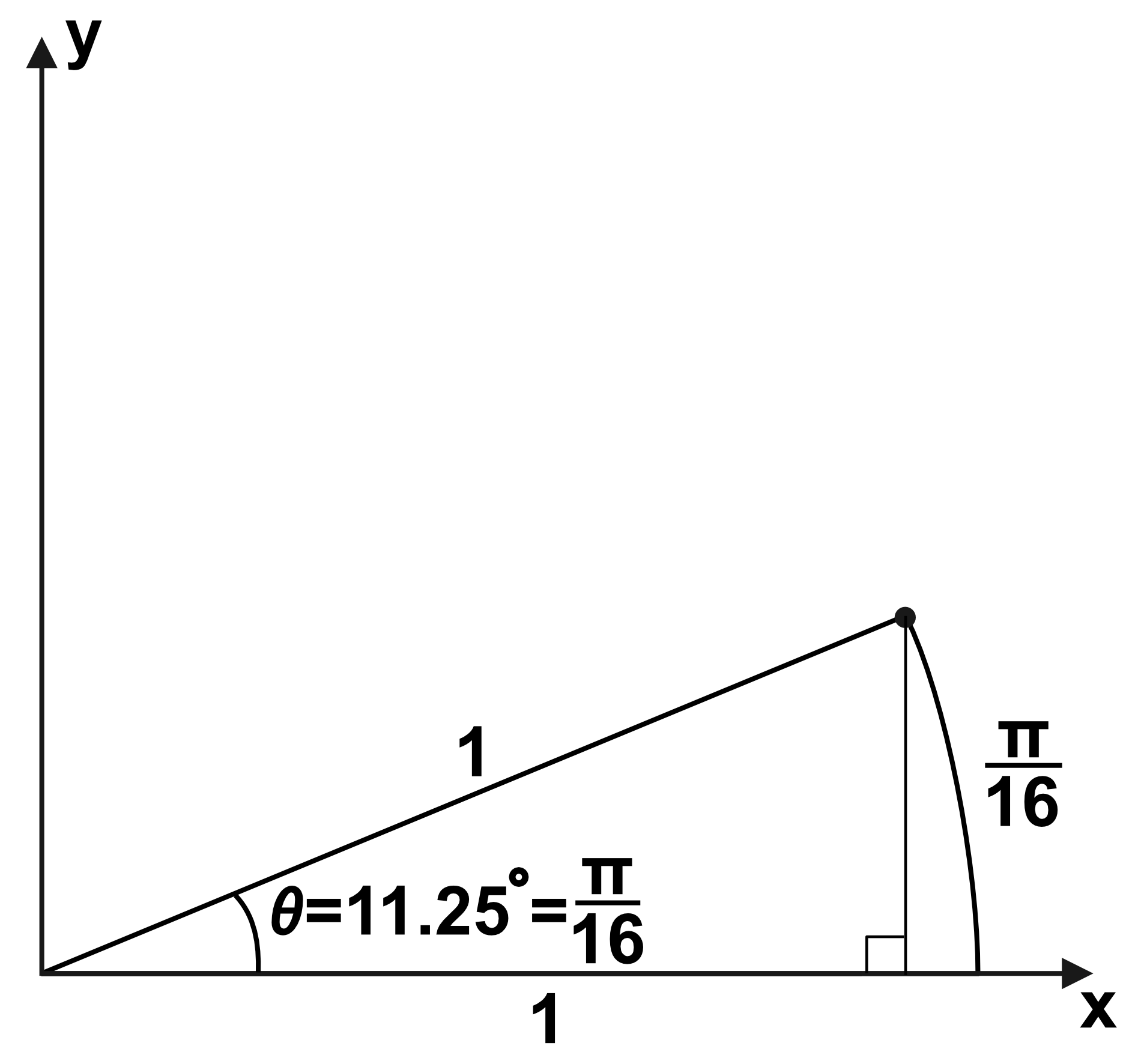
$\frac{1}{32}$ rotation corresponds to an angle of $11.25^\circ$.
The length of the radius $1$ arc created by this angle is equal to the radius $1$ circle's circumference divided by $32$:
$$L = 2\pi\frac{1}{32} = \frac{\pi}{16} = 0.1963495408...$$
Therefore, rather than calling this angle $\frac{1}{32}$ of a rotation or $11.25^\circ$, we say this angle is $\frac{\pi}{16}$ radians.
Similar to degrees, there is a straightforward conversion from rotations to radians:
Rotations to Radians: $\theta (radians) = \theta (rotations) *2\pi$

Given the above angles, we can convert rotations to degrees and radians:
$3/8\:rotation = 135^\circ = \frac{3\pi}{4}\:radians$
$1/4\:rotation = 90^\circ = \frac{\pi}{2}\:radians$
$1/8\:rotation = 45^\circ = \frac{\pi}{4}\:radians$
$1/16\:rotation = 22.5^\circ = \frac{\pi}{8}\:radians$
$1/32\:rotation = 11.25^\circ = \frac{\pi}{16}\:radians$
Radians are the more standard measure for angle, but because degrees are so common, we will utilize both units regularly in this article.
The Right Triangle
Our adventure in trigonometry begins with the right triangle. A triangle is a shape with three sides, and a right triangle is a triangle that has a $90^\circ$ angle.
Note that there are many different kinds of triangles.
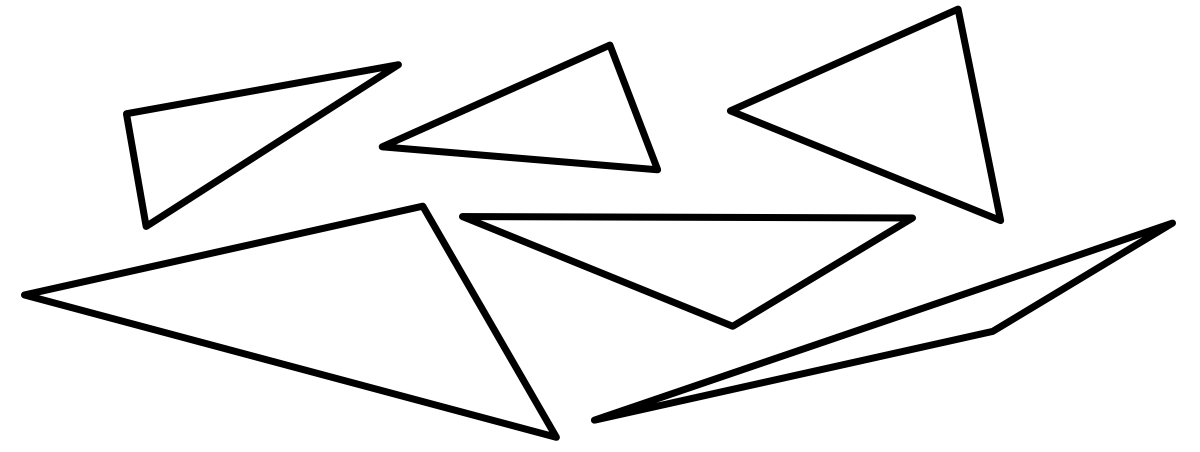
However, observe that all triangles (even right triangles) can be split in half to yield two right triangles.
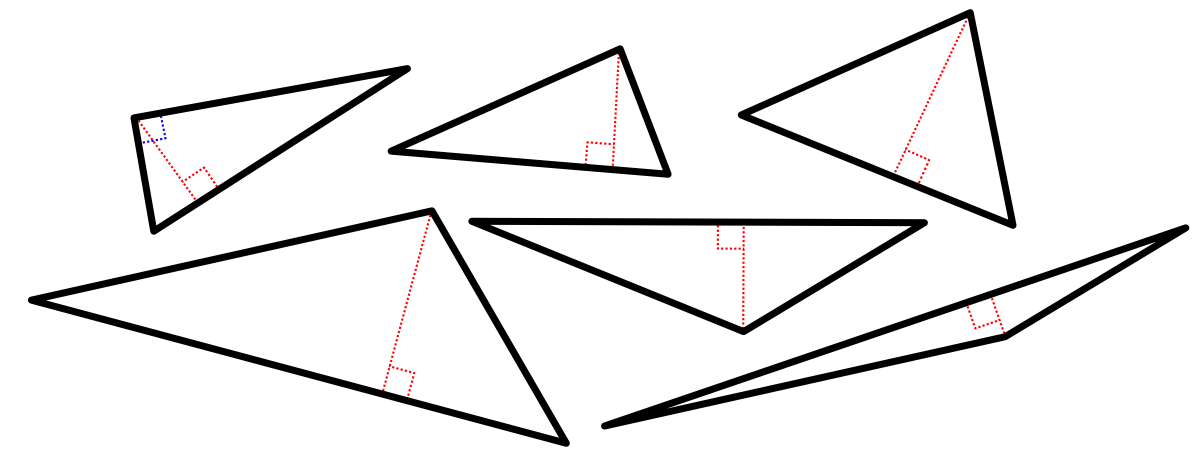
Therefore, to know right triangles is to know all triangles since all triangles are composed of right triangles.
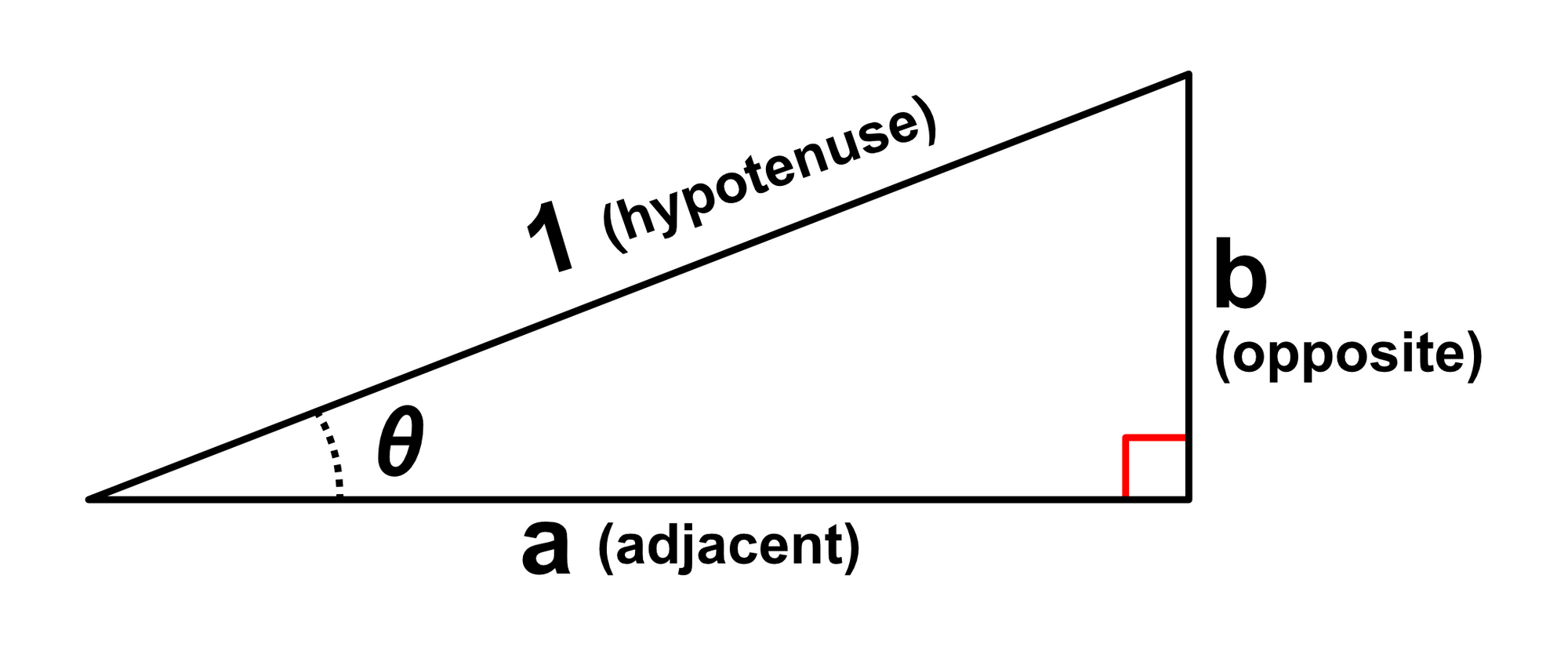
Below is an example standard right triangle. The primary angle of interest is $\theta$. The long side opposite the $90^\circ$ angle is side $c$, the hypotenuse. The side opposite the angle $\theta$ is side $b$, the opposite side. The side adjacent to the angle $\theta$ that is not the hypotenuse is side $a$, the adjacent side.
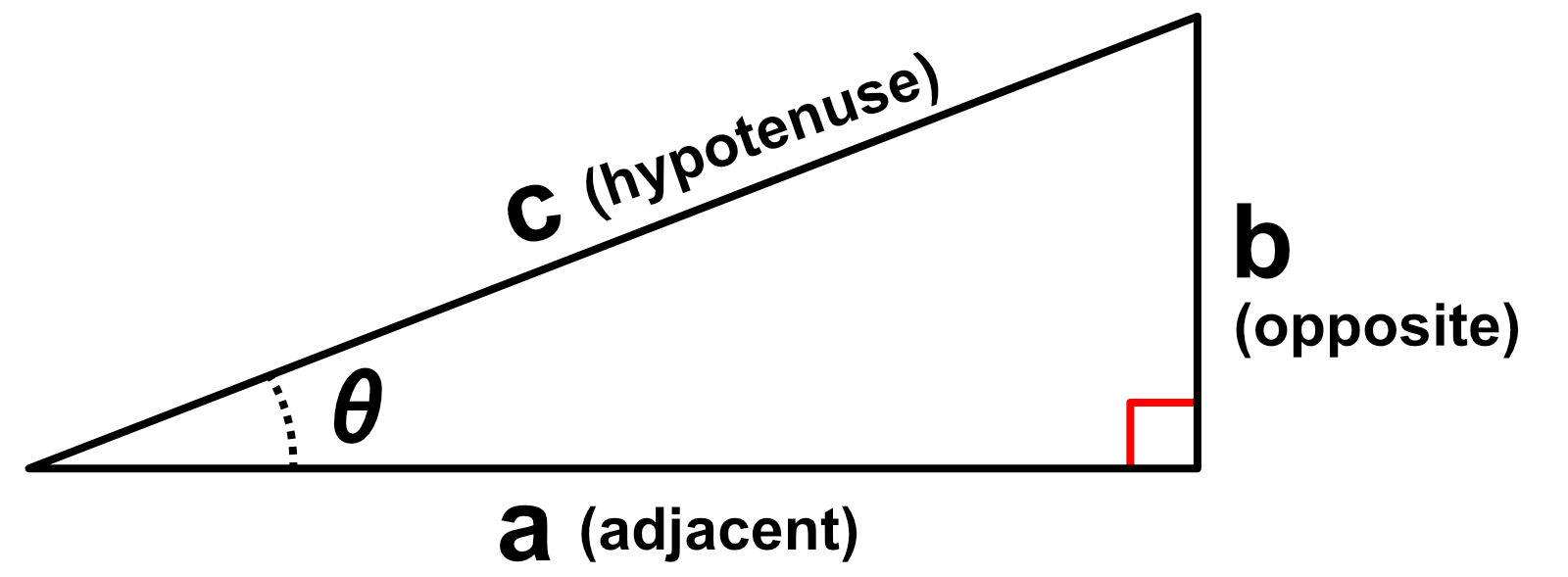
The corner containing the angle $\theta$ was chosen arbitrarily, we could have easily selected the other angle as $\theta$, but the adjacent and opposite sides would correspondingly flip.
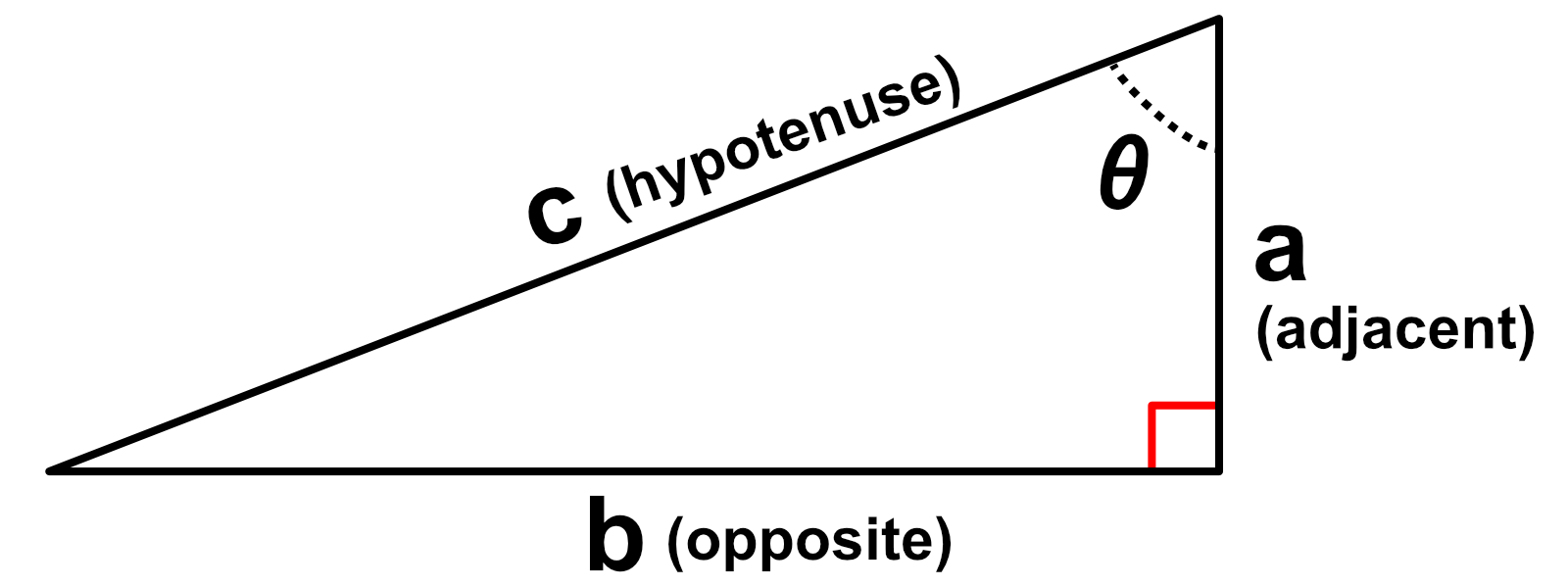
Two triangles of different size with equal angle $\theta$ are called similar triangles.
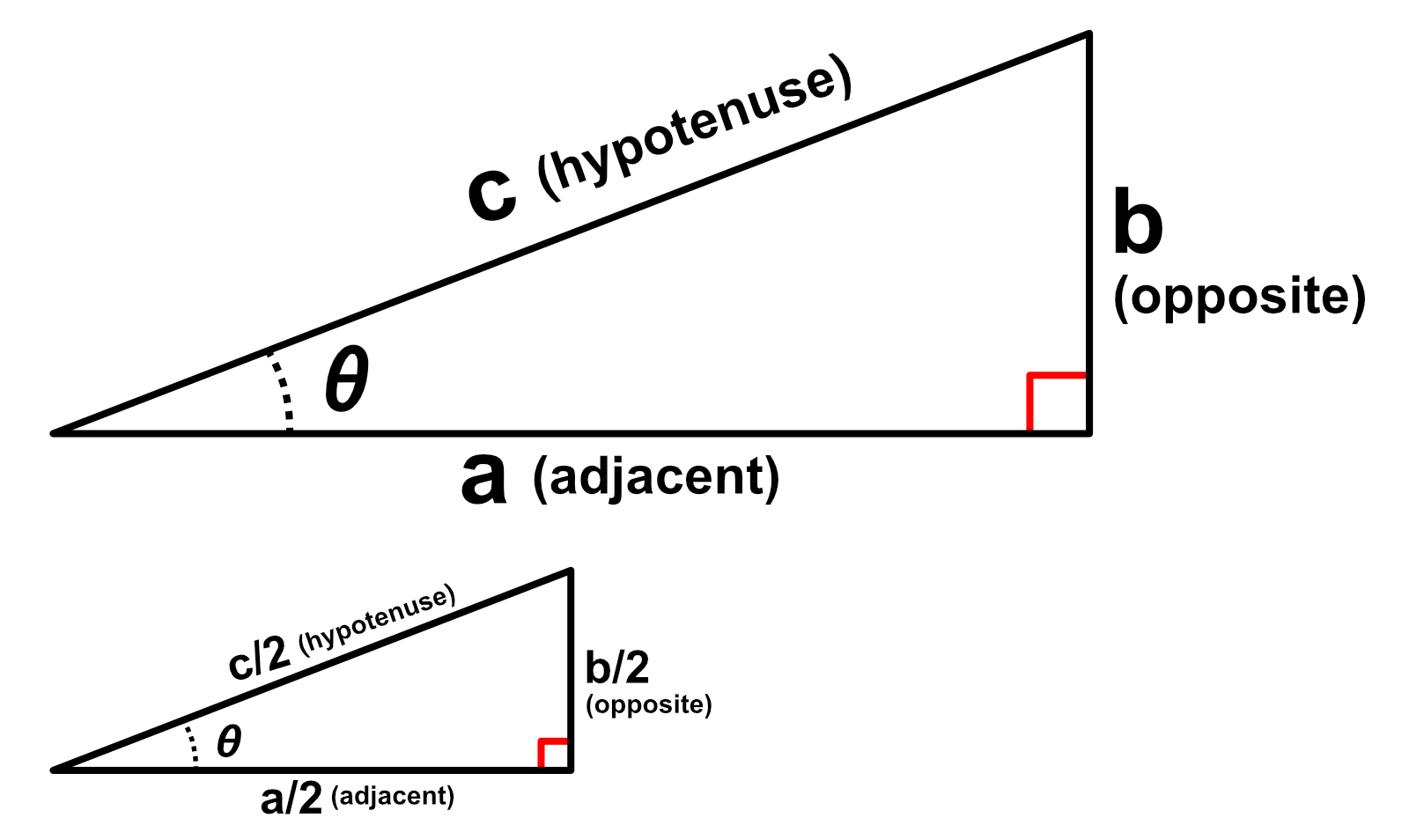
Regardless of a triangle's size, the ratio of side lengths for all triangles with a given angle is a constant. Each ratio has a special name:
$\frac{b}{c} = \frac{\frac{b}{2}}{\frac{c}{2}} = sine = \frac{opposite}{hypotenuse}$
$\frac{a}{c} = \frac{\frac{a}{2}}{\frac{c}{2}} = cosine = \frac{adjacent}{hypotenuse}$
$\frac{b}{a} = \frac{\frac{b}{2}}{\frac{a}{2}} = tangent = \frac{opposite}{adjacent}$
Sine is often abbreviated as $sin$, cosine as $cos$, and tangent as $tan$.
A helpful method of remembering these ratios is the phrase SOHCAHTOA:
$\textbf{s}ine = \frac{\textbf{o}pposite}{\textbf{h}ypotenuse}\: [SOH]$
$\textbf{c}osine = \frac{\textbf{a}djacent}{\textbf{h}ypotenuse}\: [CAH]$
$\textbf{t}angent = \frac{\textbf{o}pposite}{\textbf{a}djacent}\: [TOA]$
Because SOHCAHTOA sort of sounds like a Native American name (Sacagawea was a 19th century Native American woman), many math teachers in the United States tell their students politically insensitive stories to give the phrase flavor and attempt to improve memorization. I will spare you this experience...
The Pythagorean Theorem
Suppose that we have a triangle with side lengths $a$ and $b$.

By inspection, we can see that if the lengths of $a$ and $b$ are fixed, then the length of $c$ is also fixed. How do we calculate the length of the hypotenuse $c$?
The pythagorean theorem states:
$$a^2 + b^2 = c^2$$
The proof of this theorem is very straightforward. All we need to know is that the area of a square with side length $d$ is $A_{square} = d^2$ and the area of a triangle with side lengths $a$ and $b$ is $A_{triangle} = \frac{ab}{2}$:
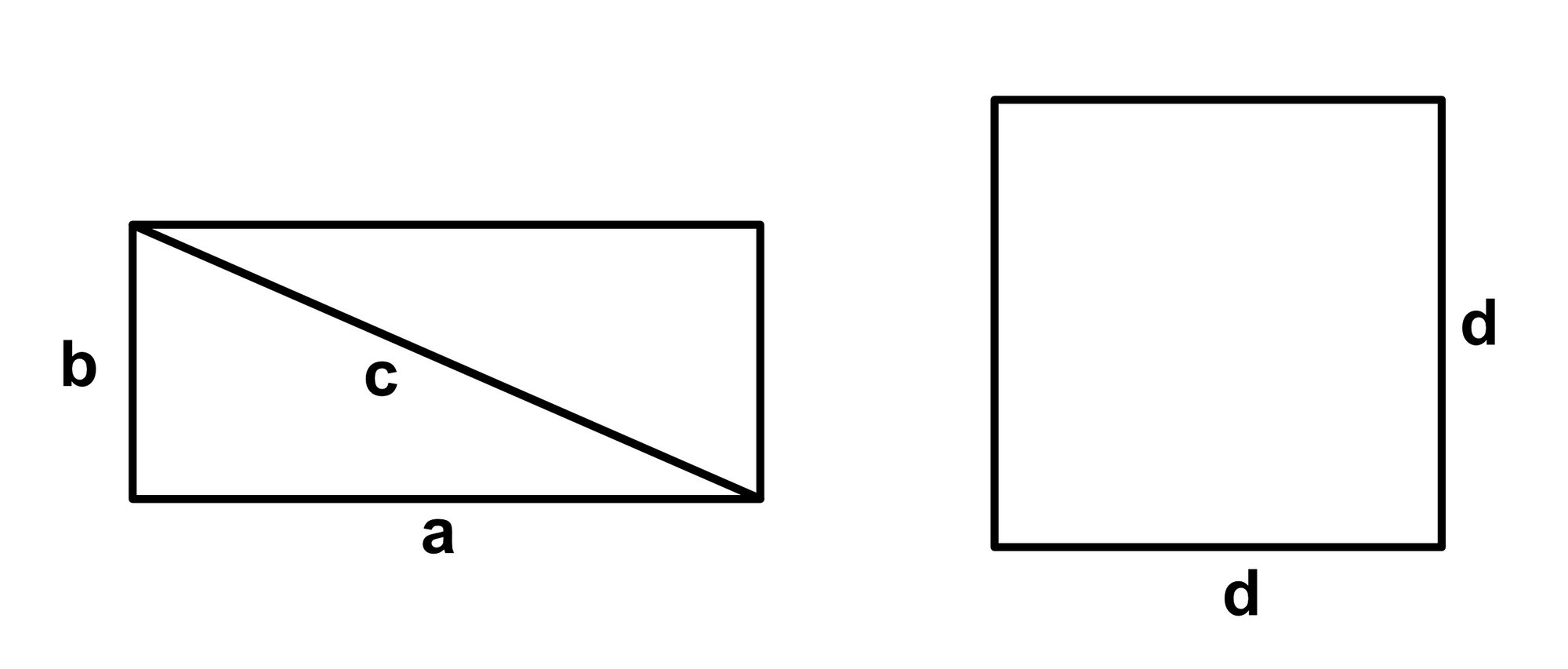
Consider we have a right triangle, we copy it four times, and arrange them to appear as a square, as shown below.
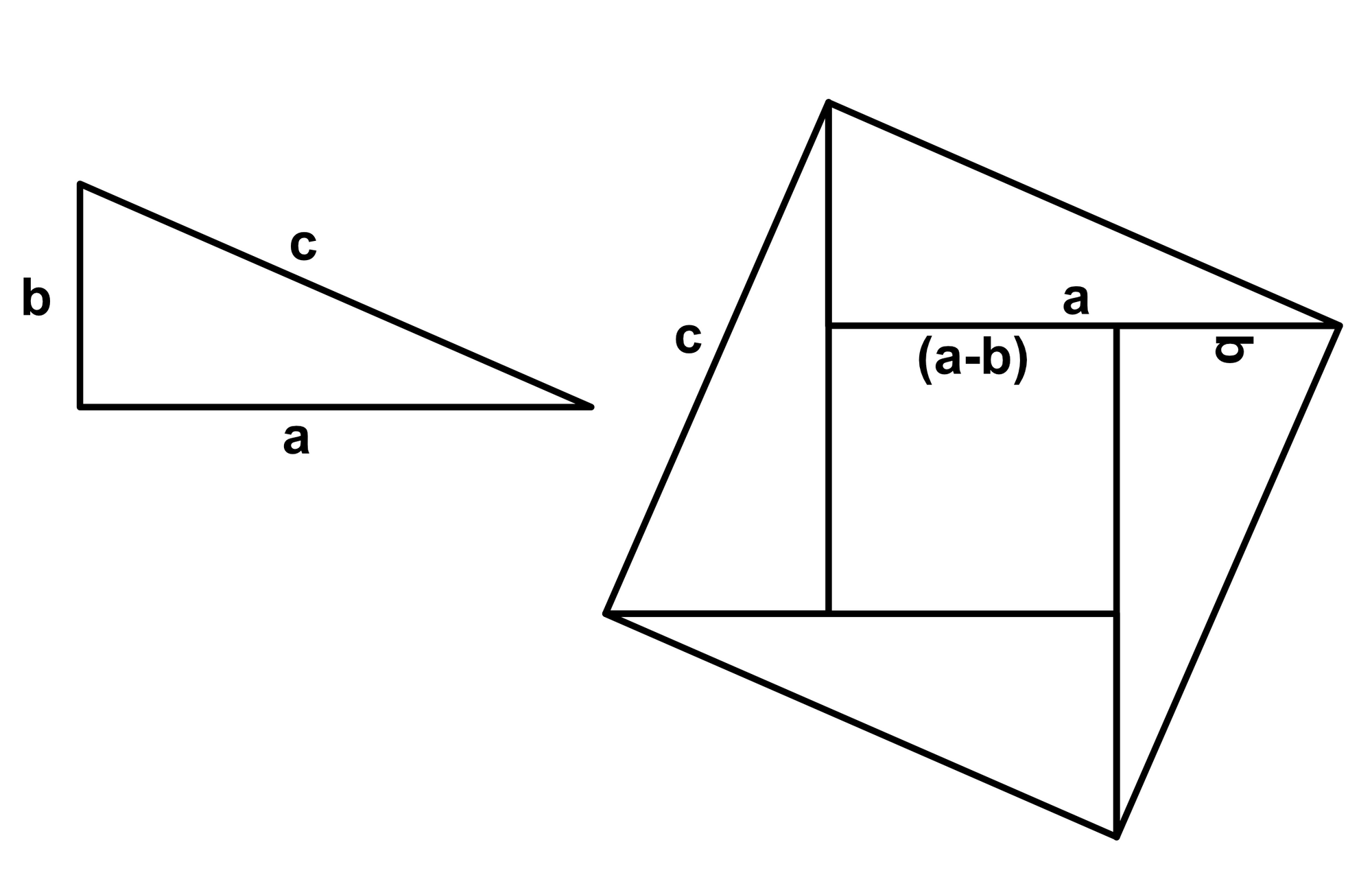
The area of the outer square is $c^2$. The area of the inner square is $(a-b)^2$. The area of each triangle is $\frac{ab}{2}$. The area of the inner square and the four triangles add up to equal the area of the outer square:
$$c^2 = (a-b)^2 + 4\frac{ab}{2}$$
$$\downarrow$$
$$c^2 = a^2 -2ab + b^2 + 4\frac{ab}{2}$$
$$\downarrow$$
$$c^2 = a^2 -2ab + b^2 + 2ab$$
$$\downarrow$$
$$c^2 = a^2 + b^2$$
$$\downarrow$$
$$\boxed{a^2 + b^2 = c^2}$$
Triangle Side Lengths from the Pythagorean Theorem
Suppose we have a right triangle, but we only know two of the side lengths.

We can do algebraic manipulation on the pythagorean theorem to isolate $c$
$$a^2 + b^2 = c^2$$
$$\downarrow$$
$$c^2 = a^2 + b^2$$
$$\downarrow$$
$$c = \pm \sqrt{a^2 + b^2}$$
$$\text{Because the length $c$ must be positive}$$
$$\downarrow$$
$$\boxed{c = \sqrt{a^2 + b^2}}$$
Through a similar process, we can arrive at:
$$a = \sqrt{c^2 - b^2}$$
$$b = \sqrt{c^2 - a^2}$$
Triangle Examples
Consider the below triangle examples.
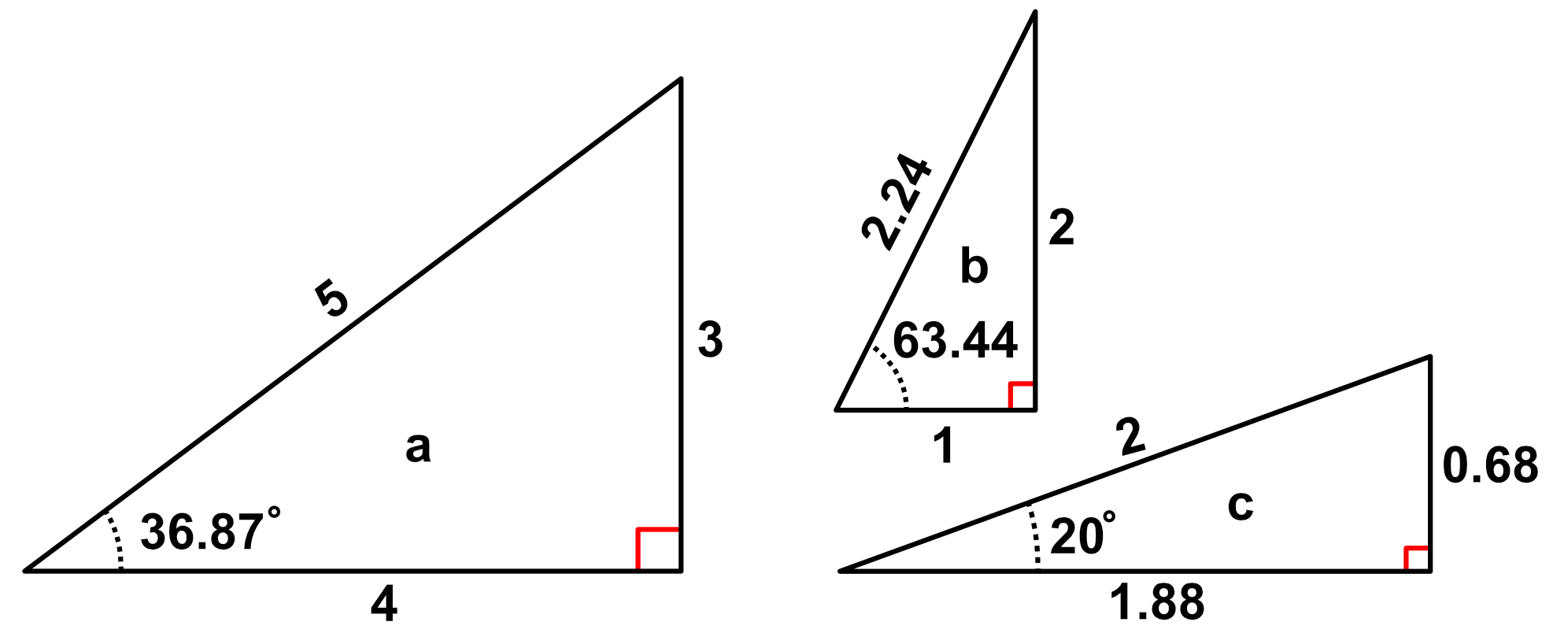
Let's calculate the sine, cosine, and tangent of triangle $a$:
$sin_{triangle\:a} = \frac{opposite}{hypotenuse} = \frac{3}{5} = 0.6$
$cos_{triangle\:a}= \frac{adjacent}{hypotenuse} = \frac{4}{5} = 0.8$
$tan_{triangle\:a} = \frac{opposite}{adjacent} = \frac{3}{4} = 0.75$
Consider triangle $A$, which is just triangle $a$ scaled by 3:
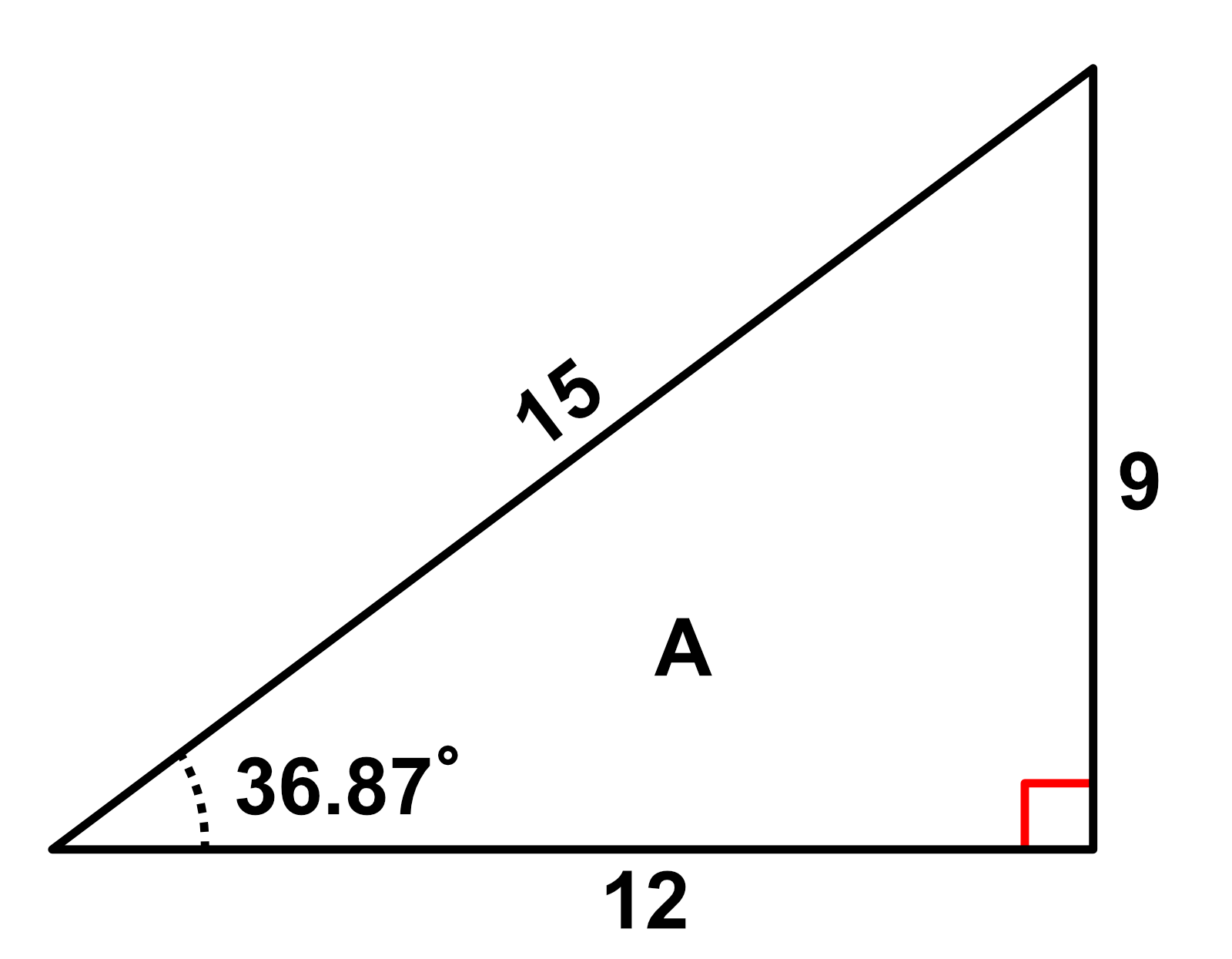
Let's calculate the sine, cosine, and tangent of triangle $A$:
$sin_{triangle\:a} = \frac{opposite}{hypotenuse} = \frac{9}{15} = 0.6$
$cos_{triangle\:a}= \frac{adjacent}{hypotenuse} = \frac{12}{15} = 0.8$
$tan_{triangle\:a} = \frac{opposite}{adjacent} = \frac{9}{12} = 0.75$
We obtain the same answer!
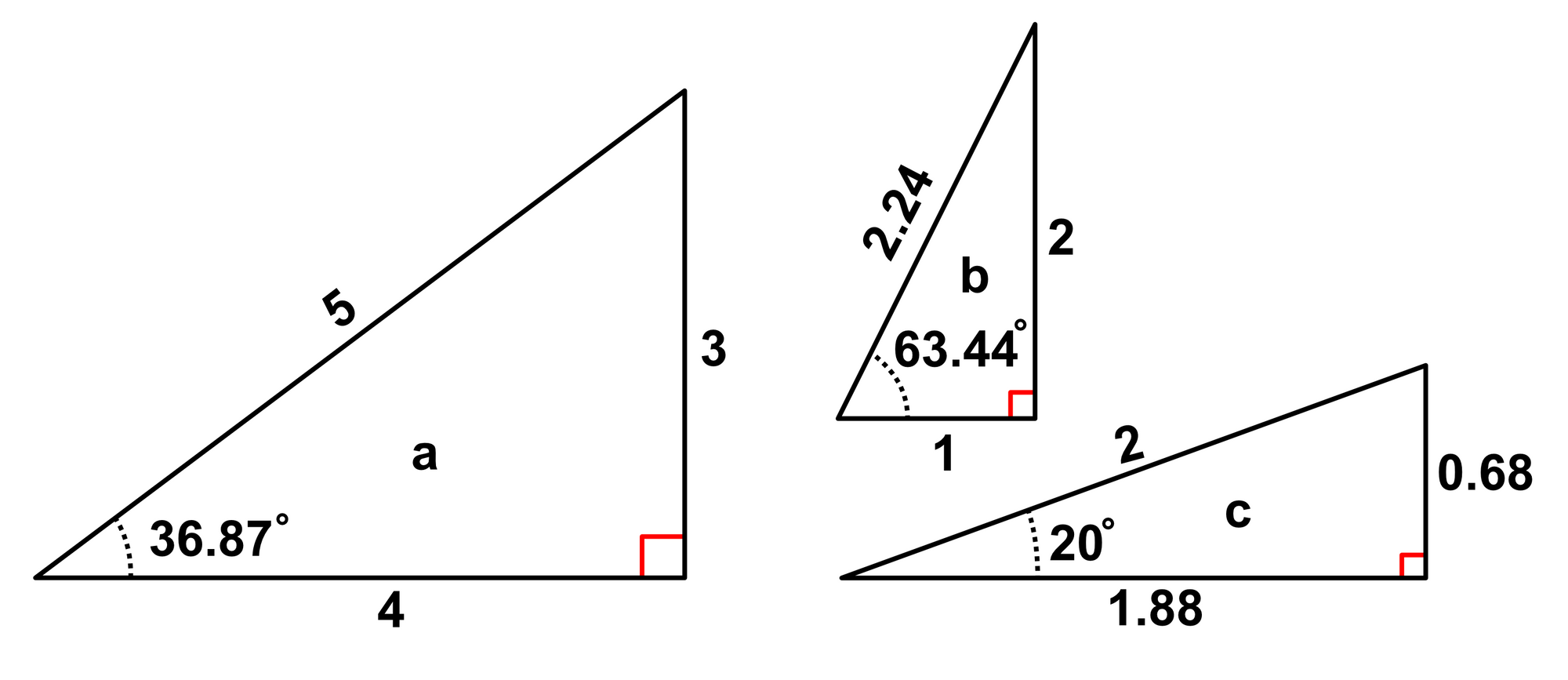
Let's calculate the sine, cosine, and tangent of triangle $b$. Note that the diagram has trunctated the value of the hypotenuse from $2.23606797749978969640...$ to $2.24$. For this exercise, we will maintain just 2 digits of precision.
The sin of triangle $b$ is:
$sin_{triangle\:b} = \frac{2}{2.24} = 0.89$
$cos_{triangle\:b} = \frac{1}{2.24} = 0.45$
$tan_{triangle\:b} = \frac{2}{1} = 2$
These are completely different values than triangle $a$, but if we were to scale triangle $b$ larger to triangle $B$, we would obtain the same values for the sine, cosine, and tangent for $b$ and $B$.
Though triangles $a$ and $A$ have different side lengths, they have the same angle $\theta_a$. Though triangles $b$ and $B$ have different side lengths, they have the same angle $\theta_b$. The angles of the two triangles are not equal, $\theta_a \ne \theta_b$. Instead of strictly thinking about sine, cosine, and tangent as the ratio of a triangle's sides, we can think about these as functions of an angle.
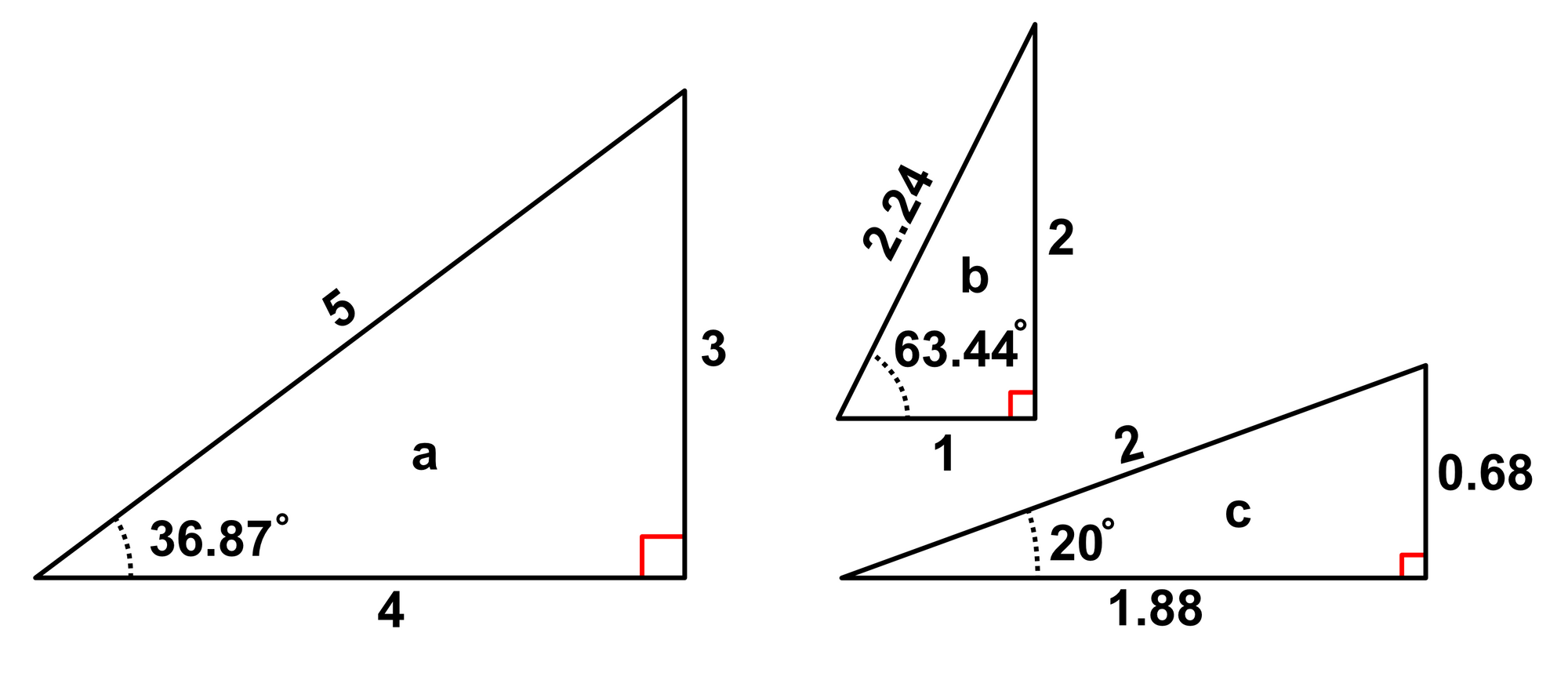
Consider triangle $a$, with an angle of $36.87$ degrees ($36.87^\circ$).
Instead of writing $sin_{triangle\:a} = \frac{9}{15} = 0.6$, we could write $sin_{36.87^\circ triangle} = \frac{opposite}{hypotenuse} = \frac{3}{5} = 0.6$ or more plainly, $sin(36.87) = 0.6$. For all of the trigonometric functions, this gives us:
$sin(36.87^\circ) = 0.6$
$cos(36.87^\circ) = 0.8$
$tan(36.87^\circ) = 0.75$
For triangle $b$, we obtain:
$sin(63.44^\circ) = 0.89$
$cos(63.44^\circ) = 0.45$
$tan(63.44^\circ) = 2$
For triangle $c$, we obtain:
$sin(20^\circ) = 0.34$
$cos(20^\circ) = 0.94$
$tan(20^\circ) = 0.36$
We call these functions (sine, cosine, and tangent) trigonometric functions!
Calculating Trigonometric Functions for Triangles
Suppose that we desire to evaluate $sin(\theta)$, $cos(\theta)$, and $tan(\theta)$ for any arbitrary angle $\theta$. How would we go about this? One observation we make is that two of our trigonometric ratios have the hypotenuse on the bottom.
$sine = \frac{opposite}{hypotenuse}$
$cosine = \frac{adjacent}{hypotenuse}$
Dividing is a pain, so let's define the unit triangle, which has a hypotenuse of 1.
One way we might go about calculating values for trigonometric functions would be drawing a quarter circle ($90^\circ$ angle) with radius $1$, splitting it in half, and then drawing a vertical line to make a $45^\circ$ triangle. Then we can use a precision ruler to measure the side lengths of the triangle.
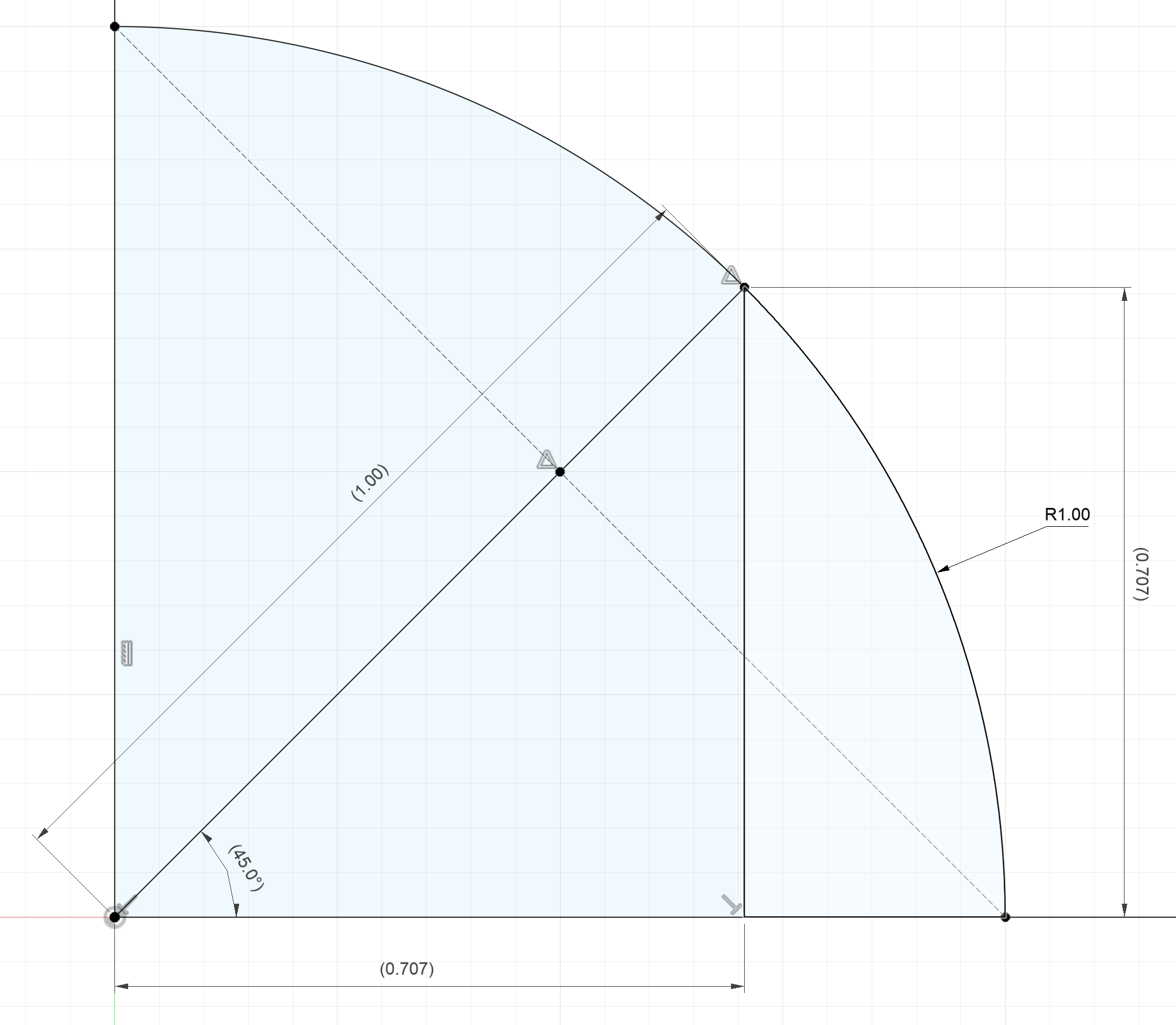
Now, knowing the side lengths, we can calculate the value for the trigonometric functions for $45^\circ$.
$sin(45) = \frac{opposite}{hypotenuse} = \frac{0.707}{1} = 0.707$
$cos(45) = \frac{adjacent}{hypotenuse} = \frac{0.707}{1} = 0.707$
$tan(45) = \frac{opposite}{adjacent} = \frac{0.707}{0.707} = 1$
This subdivision process can be repeated by splitting each of the two wedges in half. We can repeat the process for as small of an angle $\theta$ we would like:
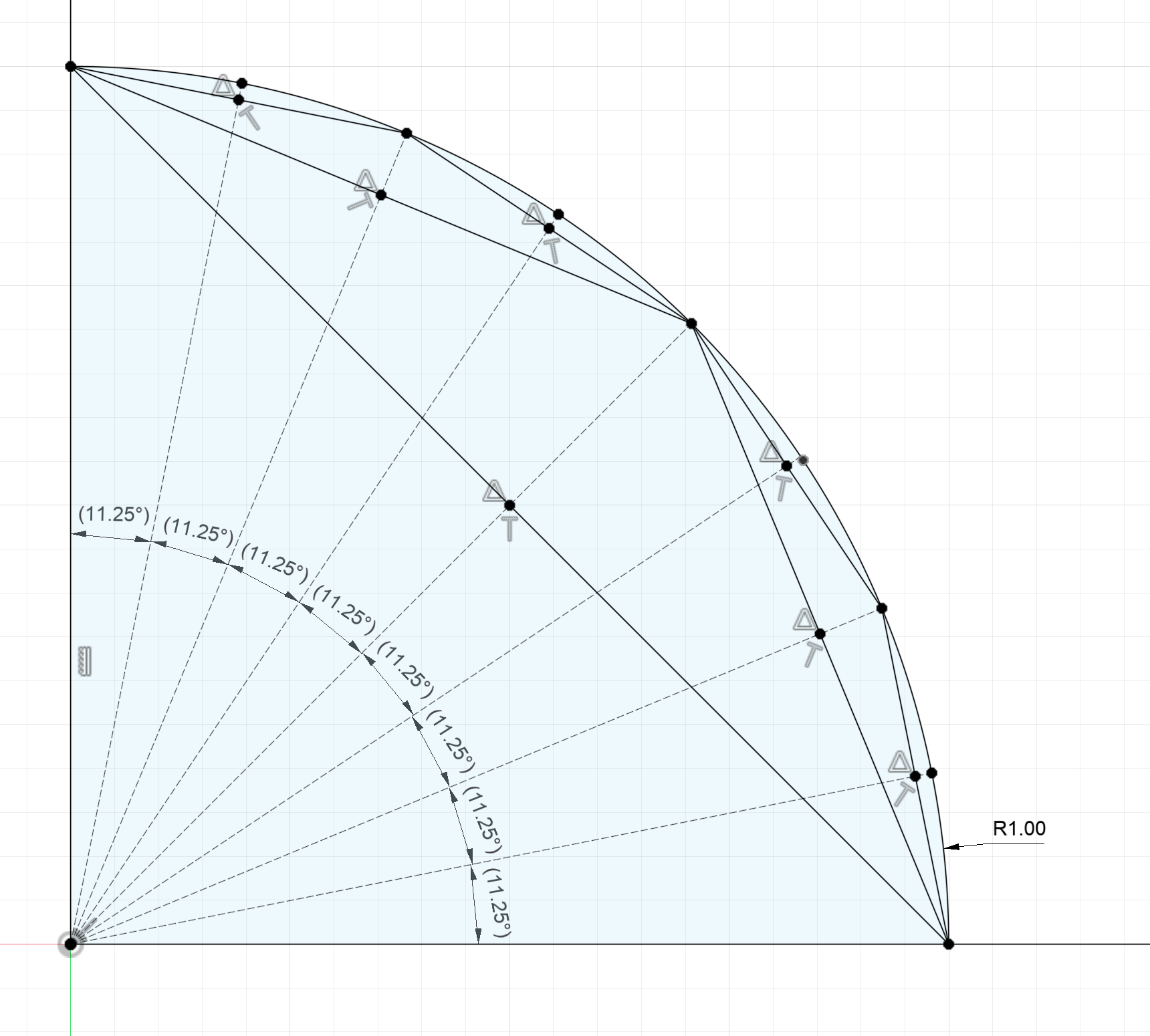
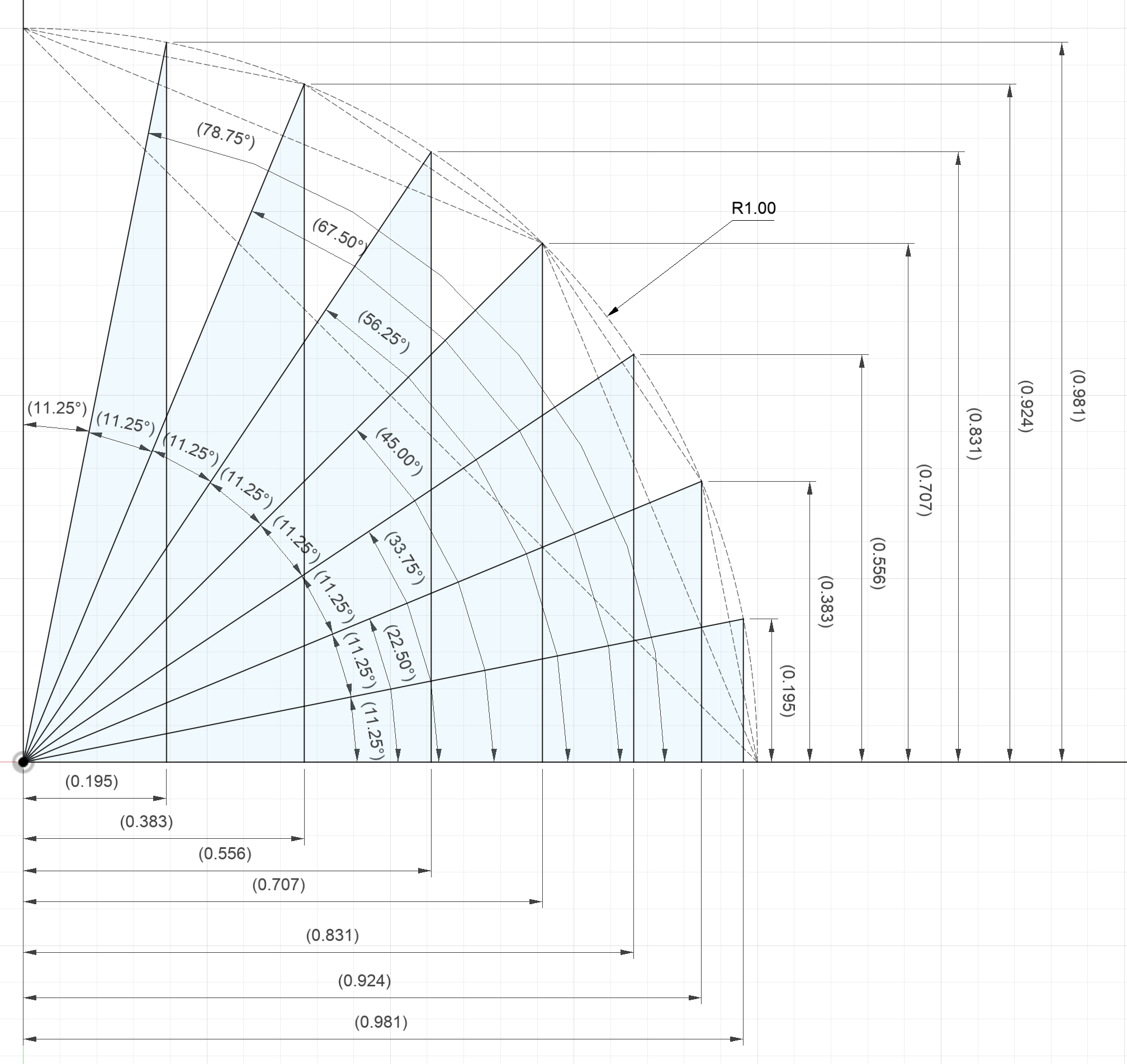
Figure 20:Left- Quarter circle segmented in to $8$ arcs | Right- Segmented quarter circle transformed into triangles
From our efforts and measurements, we can build a table that contains the values for the sin, cosine, and tangent of each angle:
| Fraction of Circle | Angle (Degrees) | Angle (Radians) | Sine | Cosine | Tangent |
|---|---|---|---|---|---|
| 1/32 | 11.25 | π/16 | 0.195 | 0.981 | 0.199 |
| 2/32 | 22.5 | π/8 | 0.383 | 0.924 | 0.415 |
| 3/32 | 33.75 | 3π/16 | 0.556 | 0.831 | 0.669 |
| 4/32 | 45 | π/4 | 0.707 | 0.707 | 1 |
| 5/32 | 56.25 | 5π/16 | 0.831 | 0.556 | 1.495 |
| 6/32 | 67.5 | 3π/8 | 0.924 | 0.383 | 2.413 |
| 7/32 | 78.75 | 7π/16 | 0.981 | 0.195 | 5.031 |
We can also plot these functions to show their general shape.
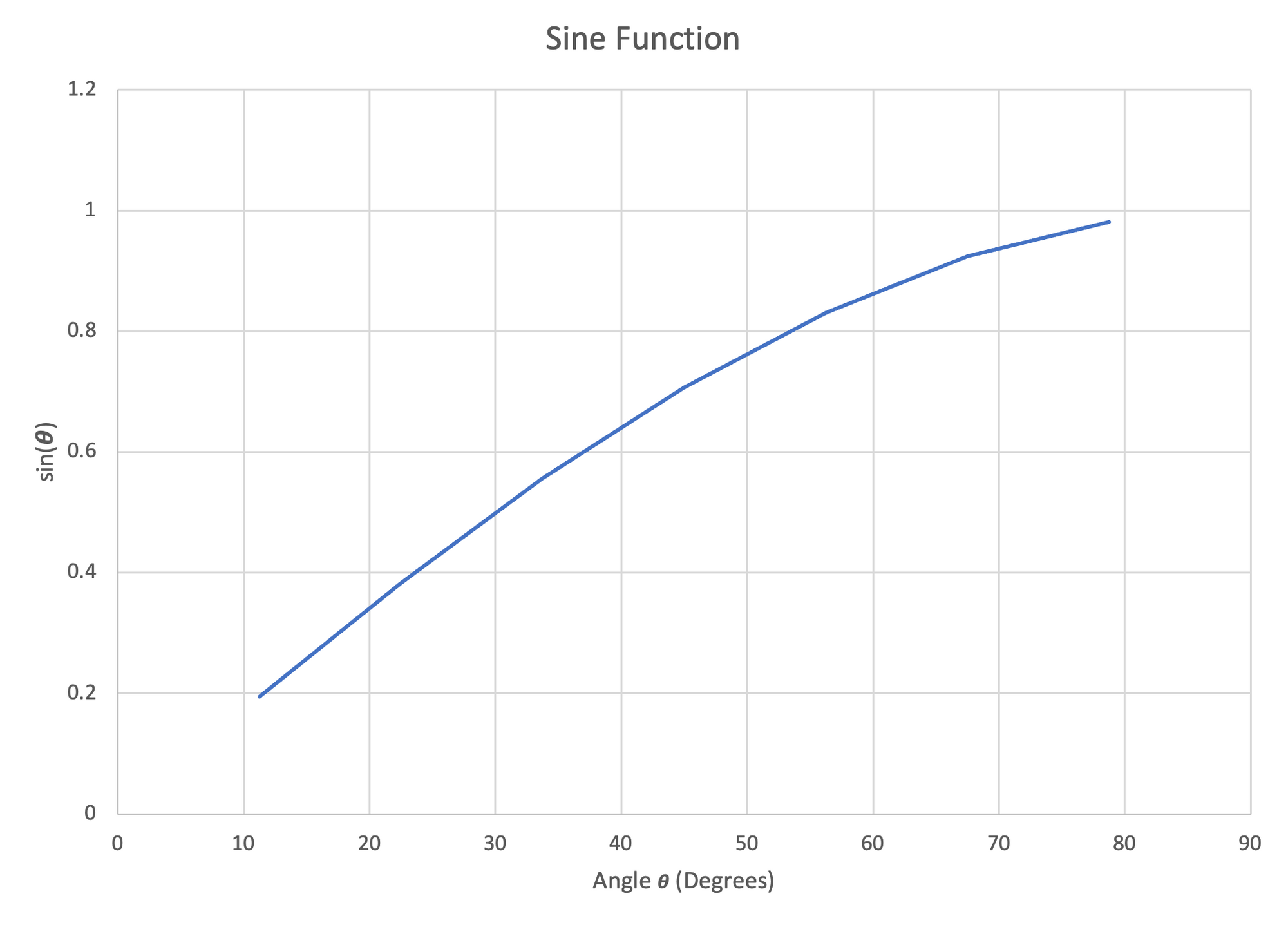
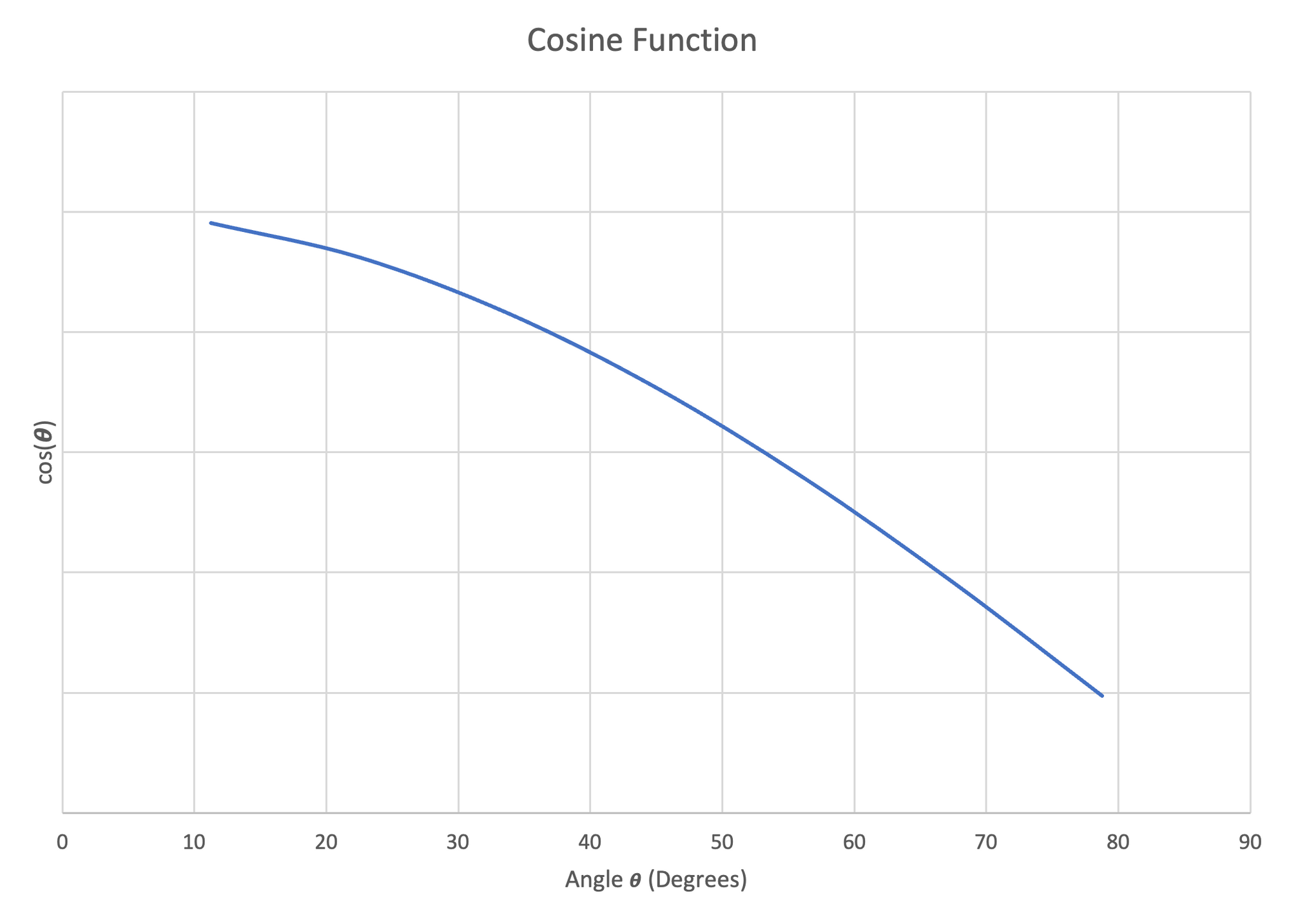
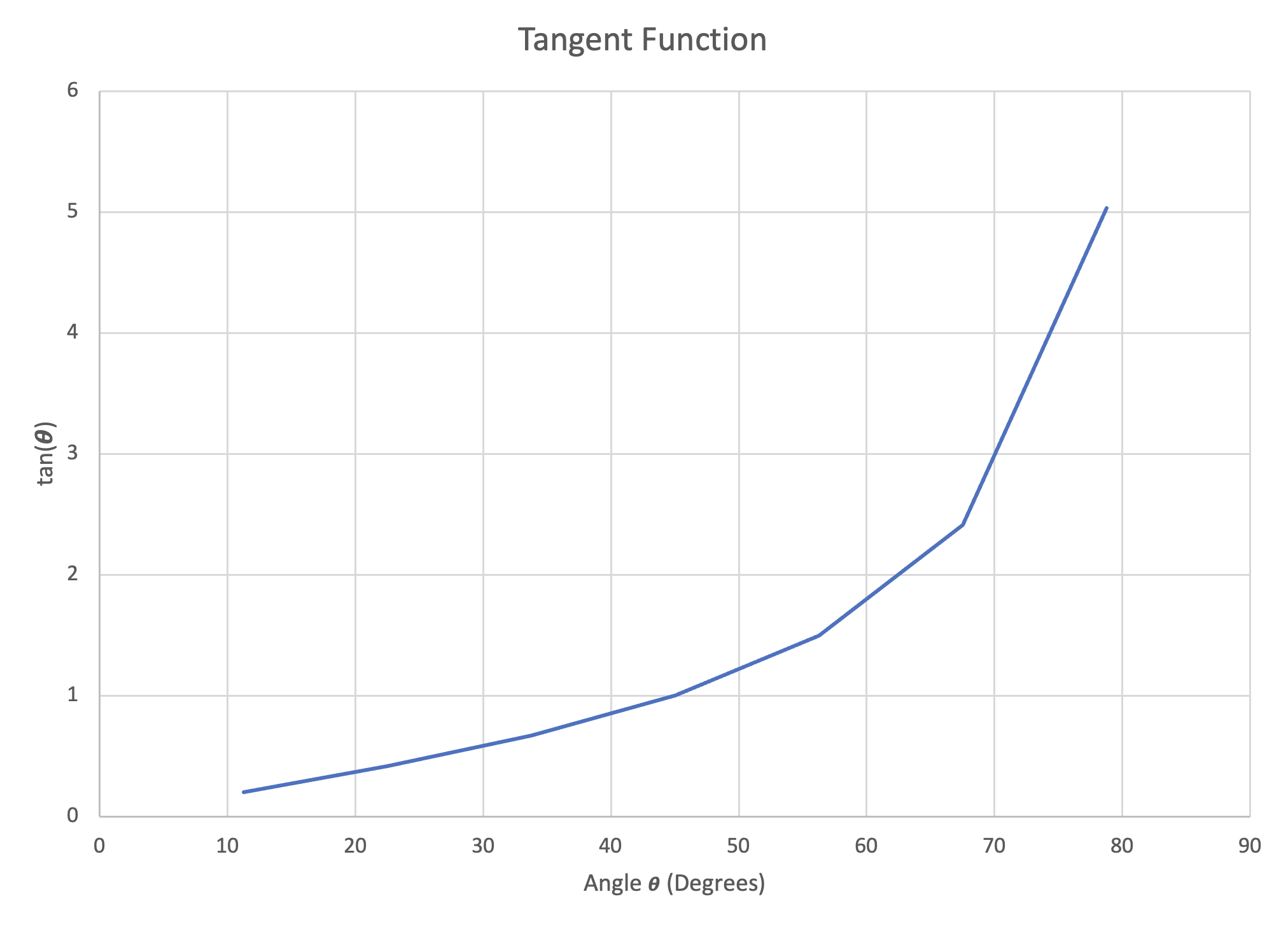
Figure 21: Left- Plot of Sine Function, $11.25^\circ-78.75^\circ$ | Center- Plot of Cosine Function, $11.25^\circ-78.75^\circ$ | Right- Plot of Tangent Function, $11.25^\circ-78.75^\circ$
The only issue with our process is that there are practical limits to how many times we can segment our quarter circle and the precision with which we can measure line lengths. There are more scalable methods but these will be left for a future discussion.
Inverse Trigonometric Functions for Triangles
As already reviewed, the sin, cosine, and tangent functions take in an angle (radians or degrees) and return a triangle's side ratio.
The inverse tangent functions $sin^{-1}$, $cos^{-1}$, $tan^{-1}$ (also called the arc tangent functions, written $arcsin$, $arccos$, $arctan$) take in a triangle's side ratio and return an angle (exactly what we were doing before but backwards). Similar to the regular trigonometric functions, the inverse trigonometric functions also have different outputs for degrees and radians. Consider once again the triangle formed by our subdivided quarter circle.

$sin^{-1}(\frac{opposite}{hypotenuse}) = sin^{-1}(0.707) = 45^\circ$
$cos^{-1}(\frac{adjacent}{hypotenuse}) = cos^{-1}(0.707) = 45^\circ$
$tan^{-1}(\frac{opposite}{adjacent}) = tan^{-1}(1) = 45^\circ$
We can apply the same segmentation methodology to arrive at the inverse trigonometric functions for many different triangles.
| Opposite/Hypotenuse | arcsine (Degrees) | arcsine (Radians) |
|---|---|---|
| 0.195 | 11.25 | π/16 |
| 0.383 | 22.5 | π/8 |
| 0.556 | 33.75 | 3π/16 |
| 0.707 | 45 | π/4 |
| 0.831 | 56.25 | 5π/16 |
| 0.924 | 67.5 | 3π/8 |
| 0.981 | 78.75 | 7π/16 |
| Adjacent/Hypotenuse | arccosine (Degrees) | arccosine (Radians) |
|---|---|---|
| 0.981 | 11.25 | π/16 |
| 0.924 | 22.5 | π/8 |
| 0.831 | 33.75 | 3π/16 |
| 0.707 | 45 | π/4 |
| 0.556 | 56.25 | 5π/16 |
| 0.383 | 67.5 | 3π/8 |
| 0.195 | 78.75 | 7π/16 |
| Opposite/Adjacent | arctangent (Degrees) | arctangent (Radians) |
|---|---|---|
| 0.199 | 11.25 | π/16 |
| 0.415 | 22.5 | π/8 |
| 0.669 | 33.75 | 3π/16 |
| 1 | 45 | π/4 |
| 1.495 | 56.25 | 5π/16 |
| 2.413 | 67.5 | 3π/8 |
| 5.031 | 78.75 | 7π/16 |
Like the regular tangent function, the inverse tangent functions can be plotted.
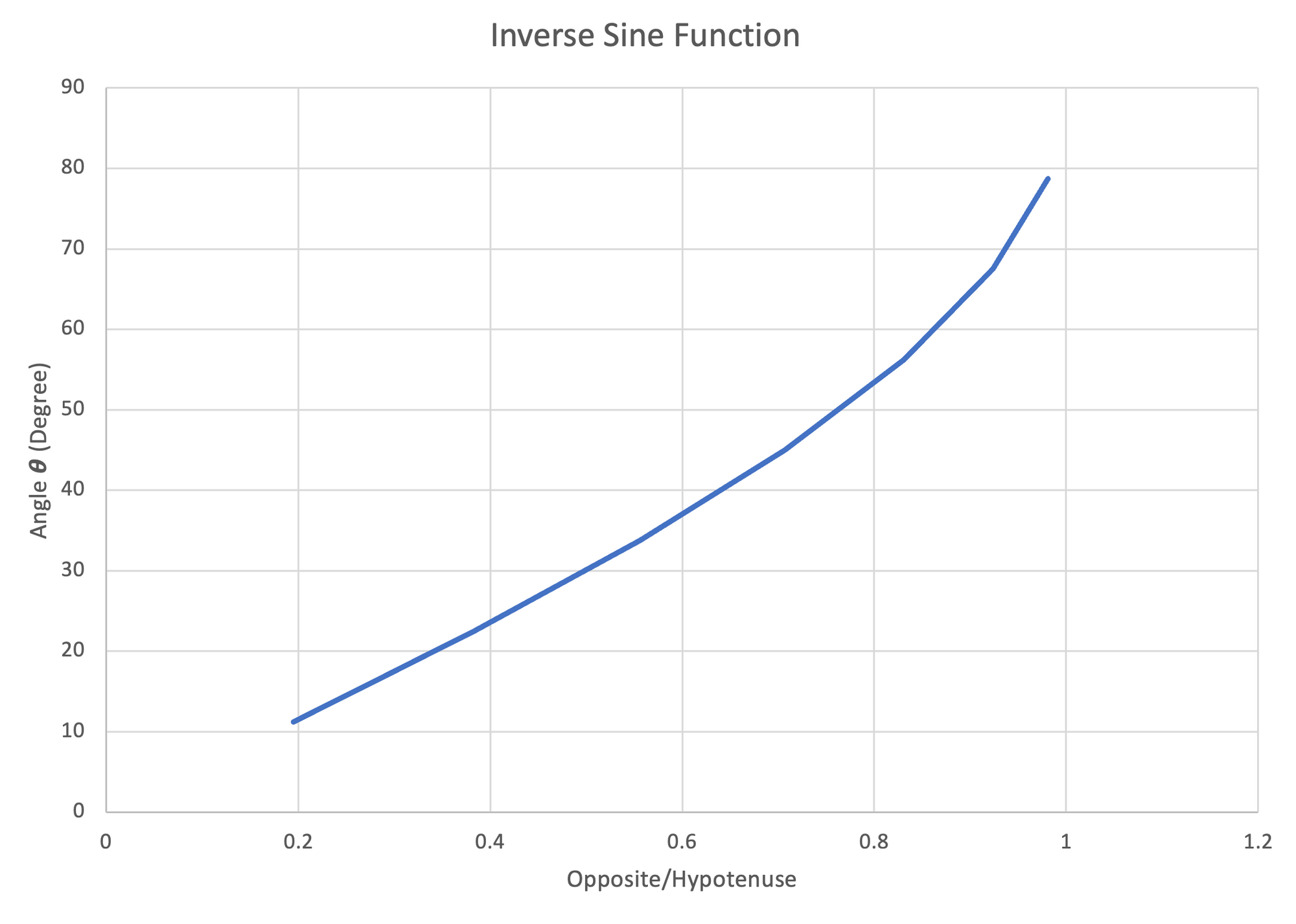
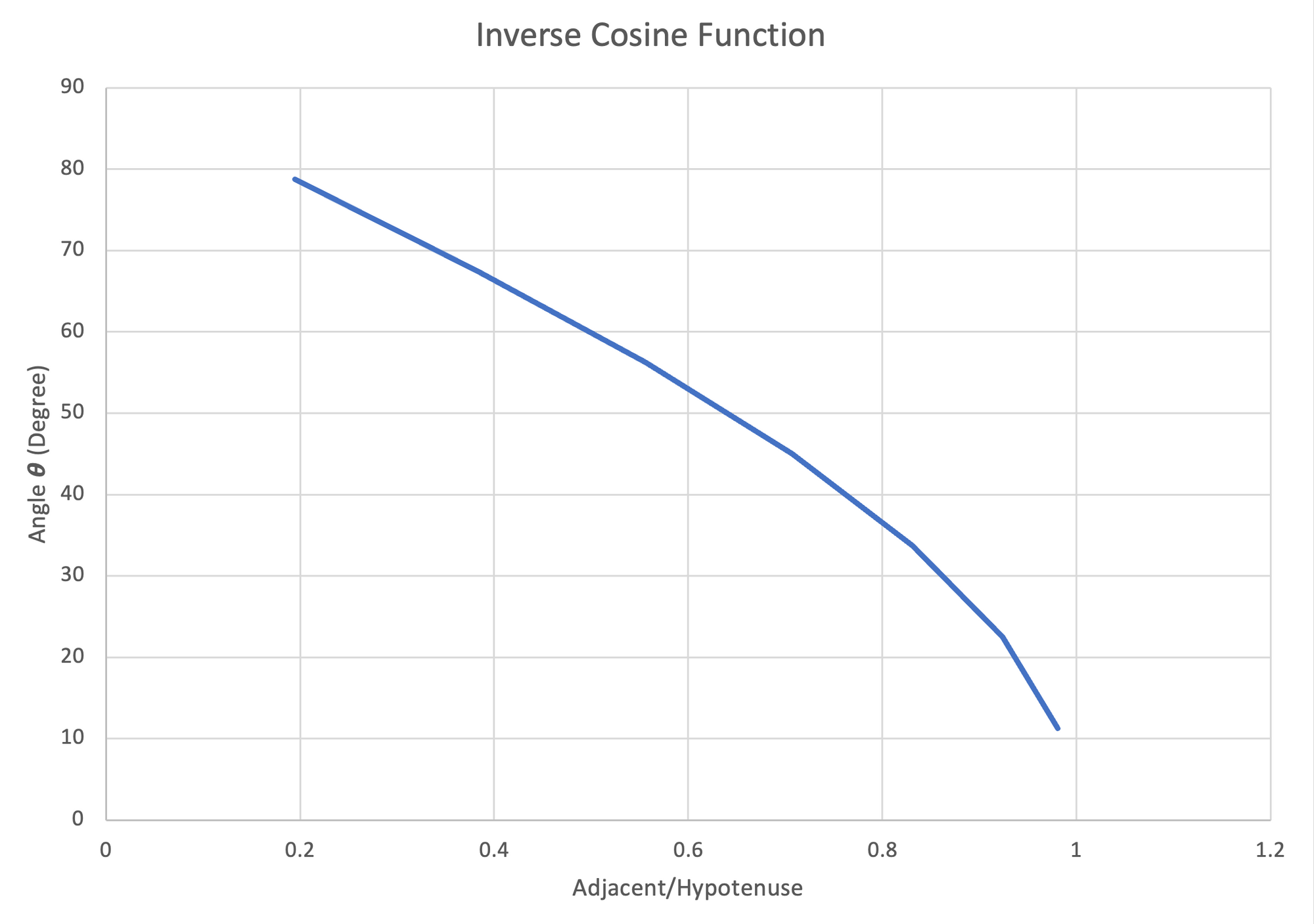
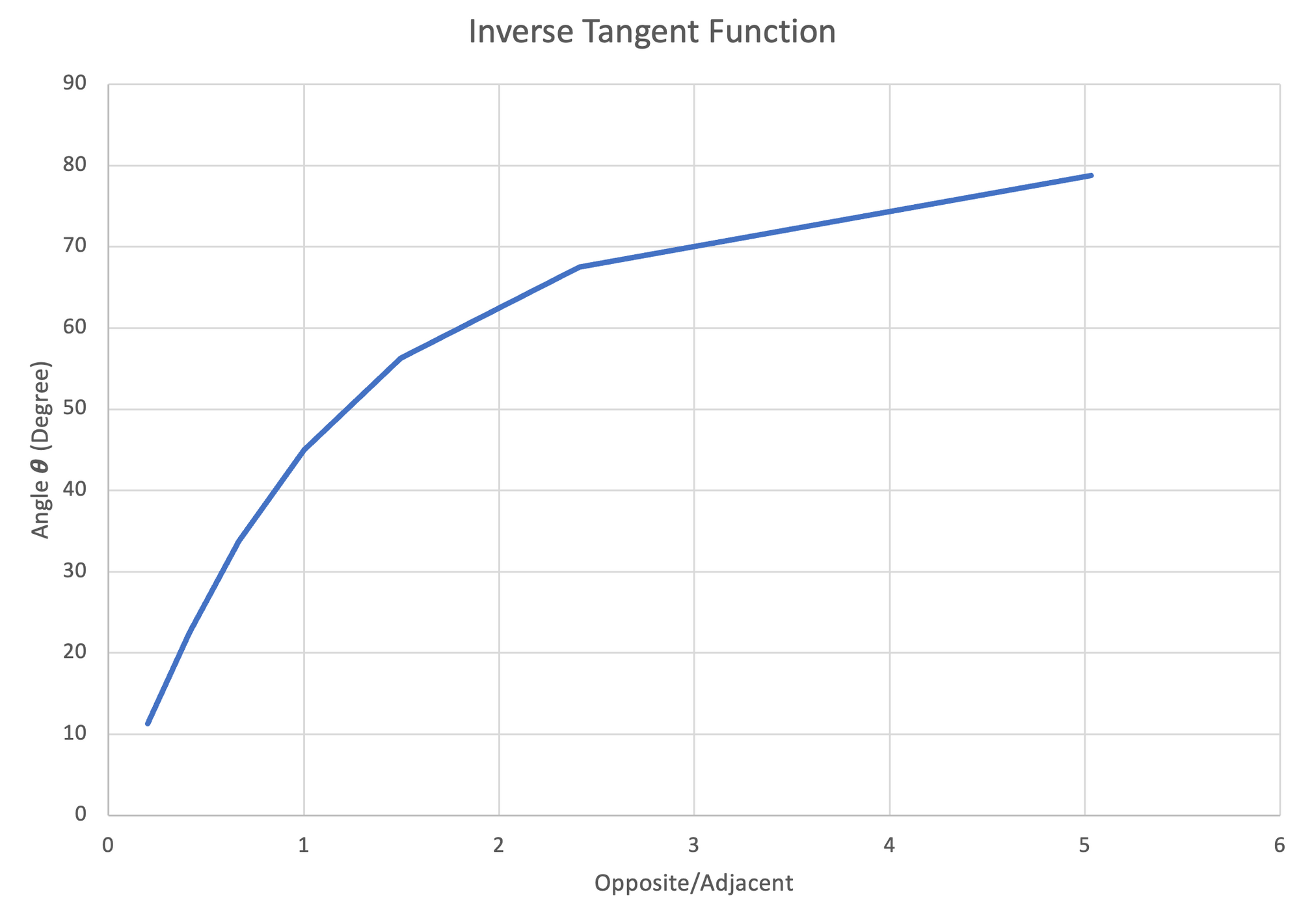
Figure 23: Left- Plot of Inverse Sine Function, $11.25^\circ-78.75^\circ$ | Center- Plot of Inverse Cosine Function, $11.25^\circ-78.75^\circ$ | Right- Plot of Inverse Tangent Function, $11.25^\circ-78.75^\circ$
The Unit Quarter Circle
Here, we make a critical observation that allows for the extension of trigonometric functions. The lengths of each triangle side corresponded to the coordinates of where that triangle touched the circle.
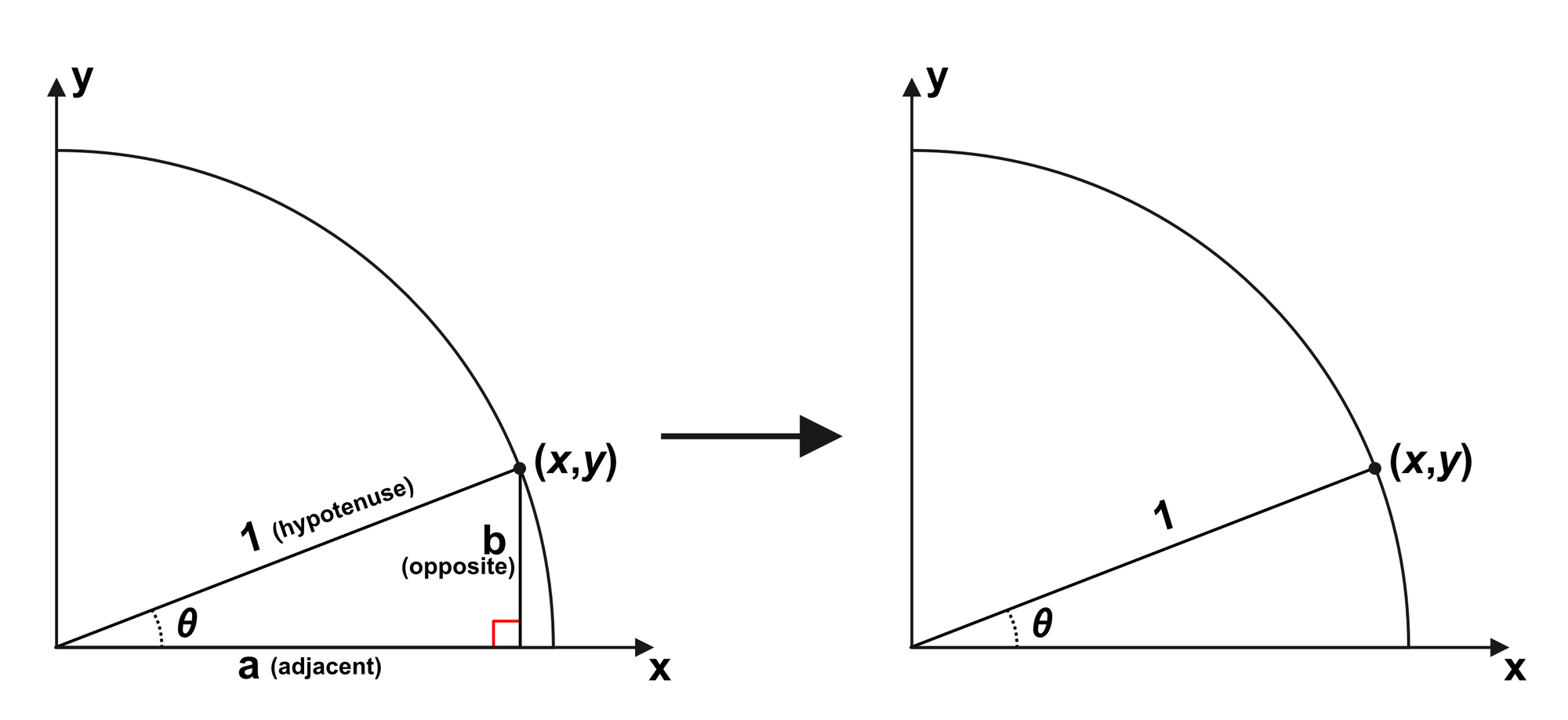
If we instead use the coordinates of an arc with radius $1$ and angle $\theta$ to define the sine, cosine and tangent, we obtain:
$sin(\theta) = y$
$cos(\theta) = x$
$tan(\theta) = \frac{y}{x}$
We can go through the same circle segmentation exercise as before, but instead we use the coordinates to build a table for the trigonometric functions.
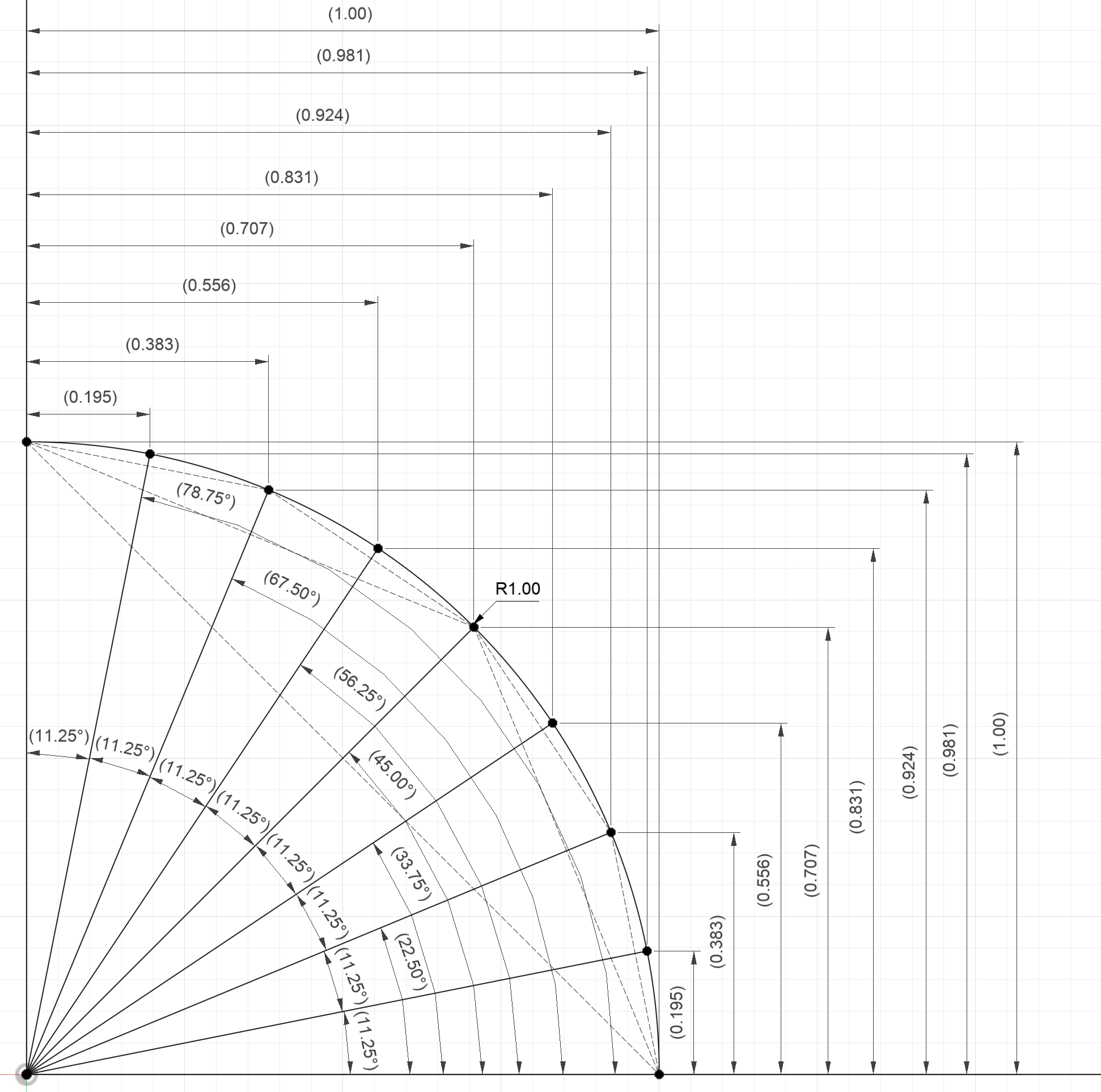
| Fraction of Circle | Angle (Degrees) | Angle (Radians) | Sine | Cosine | Tangent |
|---|---|---|---|---|---|
| 1/32 | 11.25 | π/16 | 0.195 | 0.981 | 0.199 |
| 2/32 | 22.5 | π/8 | 0.383 | 0.924 | 0.415 |
| 3/32 | 33.75 | 3π/16 | 0.556 | 0.831 | 0.669 |
| 4/32 | 45 | π/4 | 0.707 | 0.707 | 1 |
| 5/32 | 56.25 | 5π/16 | 0.831 | 0.556 | 1.495 |
| 6/32 | 67.5 | 3π/8 | 0.924 | 0.383 | 2.413 |
| 7/32 | 78.75 | 7π/16 | 0.981 | 0.195 | 5.031 |
This is of course the exact same table we generated prior using triangles, but now, it has been generated using arcs and coordinates. One immediate benefit of this perspective change is that it now makes sense to calculate the value of a trigonometric function when $\theta = 0^\circ$ or $\theta = 90^\circ$.
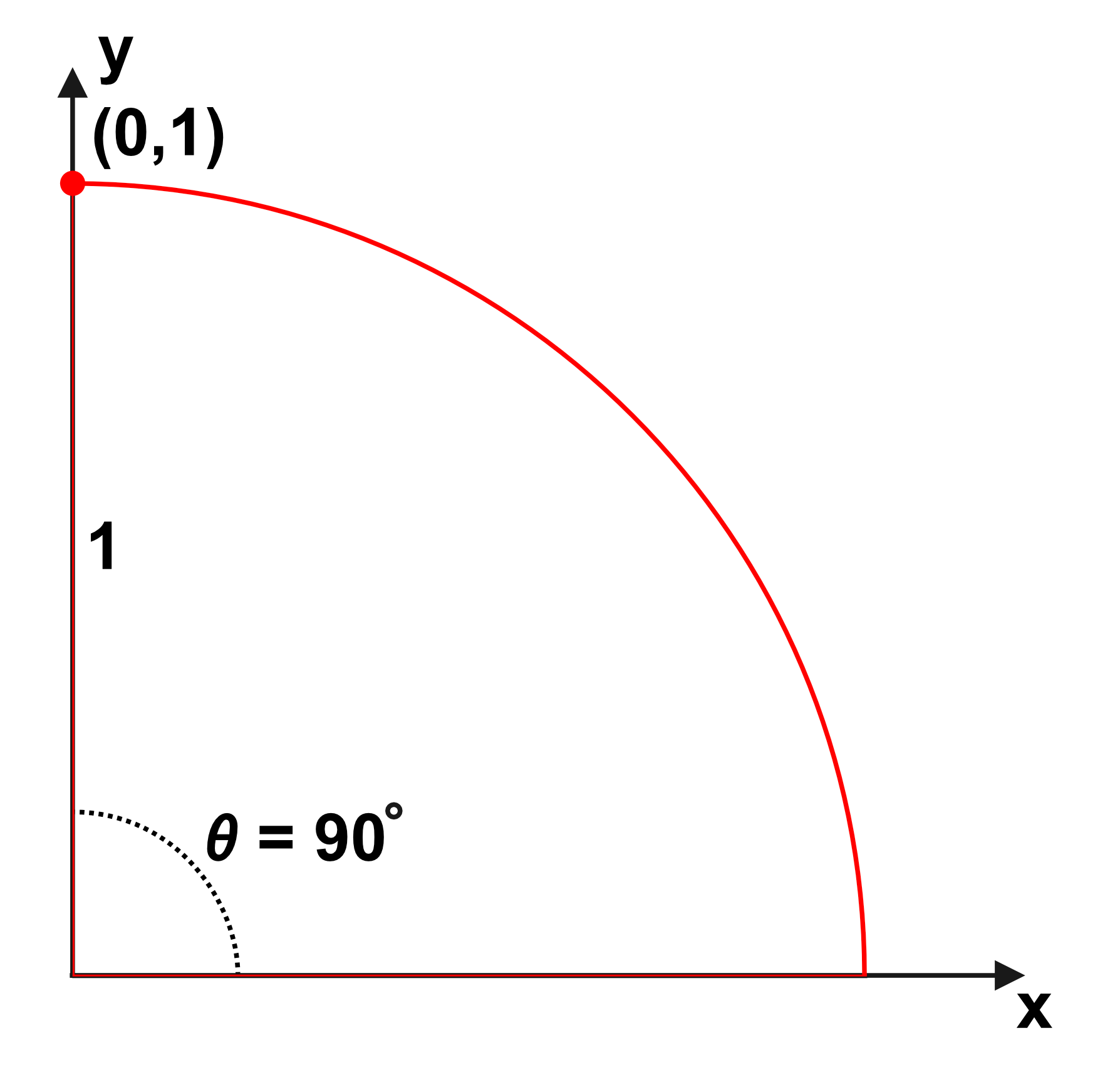
Figure 26: Extension of trigonometric functions to cover entire quarter circle Left- $0^\circ$ | Right- $90^\circ$
$sin(0^\circ) = y = 0$
$cos(0^\circ) = x = 1$
$tan(0^\circ) = \frac{0}{1} = 0$
$sin(90^\circ) = y = 1$
$cos(90^\circ) = x = 0$
$tan(90^\circ) = \frac{1}{0} = undefined$
Okay, so maybe it's a little odd that the tangent function is undefined at $90^\circ$, but let's roll with it for the time being. We can add our new values for the trigonometric functions to our table.
| Fraction of Circle | Angle (Degrees) | Angle (Radians) | Sine | Cosine | Tangent |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 1/32 | 11.25 | π/16 | 0.195 | 0.981 | 0.199 |
| 2/32 | 22.5 | π/8 | 0.383 | 0.924 | 0.415 |
| 3/32 | 33.75 | 3π/16 | 0.556 | 0.831 | 0.669 |
| 4/32 | 45 | π/4 | 0.707 | 0.707 | 1 |
| 5/32 | 56.25 | 5π/16 | 0.831 | 0.556 | 1.495 |
| 6/32 | 67.5 | 3π/8 | 0.924 | 0.383 | 2.413 |
| 7/32 | 78.75 | 7π/16 | 0.981 | 0.195 | 5.031 |
| 8/32 | 90 | π/2 | 1 | 0 | Undefined |
To really appreciate this extension of the trigonometric functions, recognize that there is no right triangle with two $90^\circ$ angles. There is also no right triangle with a $0^\circ$ angle. Our arc/circle interpretation of trigonometric functions is valid over a larger range of angle than our triangular side ratio interpretation.
Inverse Trigonometric Function for Quarter Circle
The inverse trigonometric functions extend to the segmented radius $1$ quarter circle coordinates without issue.
| Unit Quarter Circle Y | arcsine (Degrees) | arcsine (Radians) |
|---|---|---|
| 0 | 0 | 0 |
| 0.195 | 11.25 | π/16 |
| 0.383 | 22.5 | π/8 |
| 0.556 | 33.75 | 3π/16 |
| 0.707 | 45 | π/4 |
| 0.831 | 56.25 | 5π/16 |
| 0.924 | 67.5 | 3π/8 |
| 0.981 | 78.75 | 7π/16 |
| 1 | 90 | π/2 |
| Unit Quarter Circle X | arccosine (Degrees) | arccosine (Radians) |
|---|---|---|
| 1 | 0 | 0 |
| 0.981 | 11.25 | π/16 |
| 0.924 | 22.5 | π/8 |
| 0.831 | 33.75 | 3π/16 |
| 0.707 | 45 | π/4 |
| 0.556 | 56.25 | 5π/16 |
| 0.383 | 67.5 | 3π/8 |
| 0.195 | 78.75 | 7π/16 |
| 0 | 90 | π/2 |
Note that like the tangent function, the inverse tangent function also has a value for which it is undefined.
| Unit Quarter Circle Y/X | arctangent (Degrees) | arctangent (Radians) |
|---|---|---|
| 0 | 0 | 0 |
| 0.199 | 11.25 | π/16 |
| 0.415 | 22.5 | π/8 |
| 0.669 | 33.75 | 3π/16 |
| 1 | 45 | π/4 |
| 1.495 | 56.25 | 5π/16 |
| 2.413 | 67.5 | 3π/8 |
| 5.031 | 78.75 | 7π/16 |
| 1/0 | Undefined | Undefined |
The Unit Circle
Consider if we extend our definition beyond the quarter circle we used earlier and we maintain our perspective of using the coordinates of the arc's endpoint. Let's split the quarter arc in the upper left quadrant, which forms a $135^\circ$ arc.
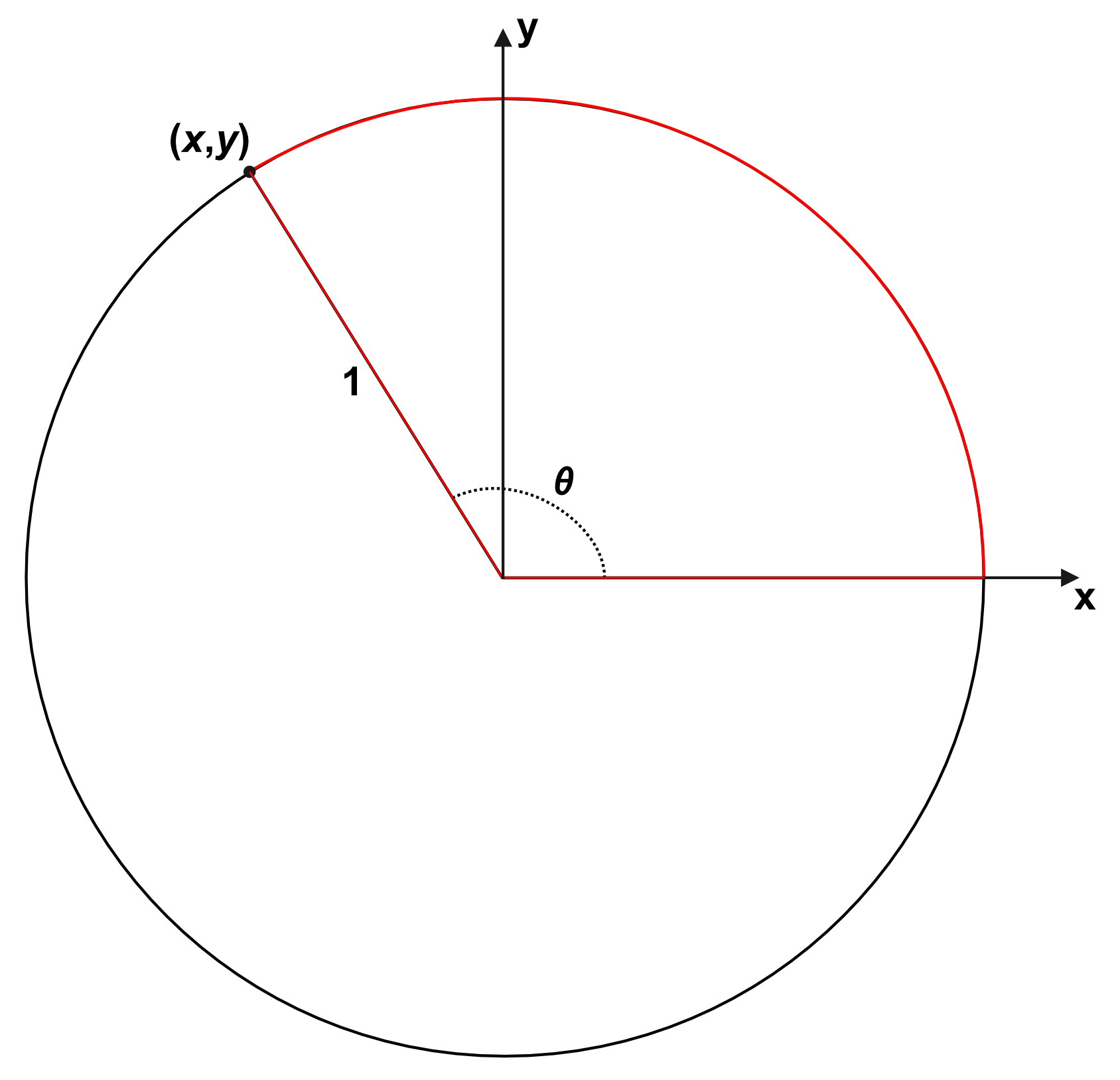
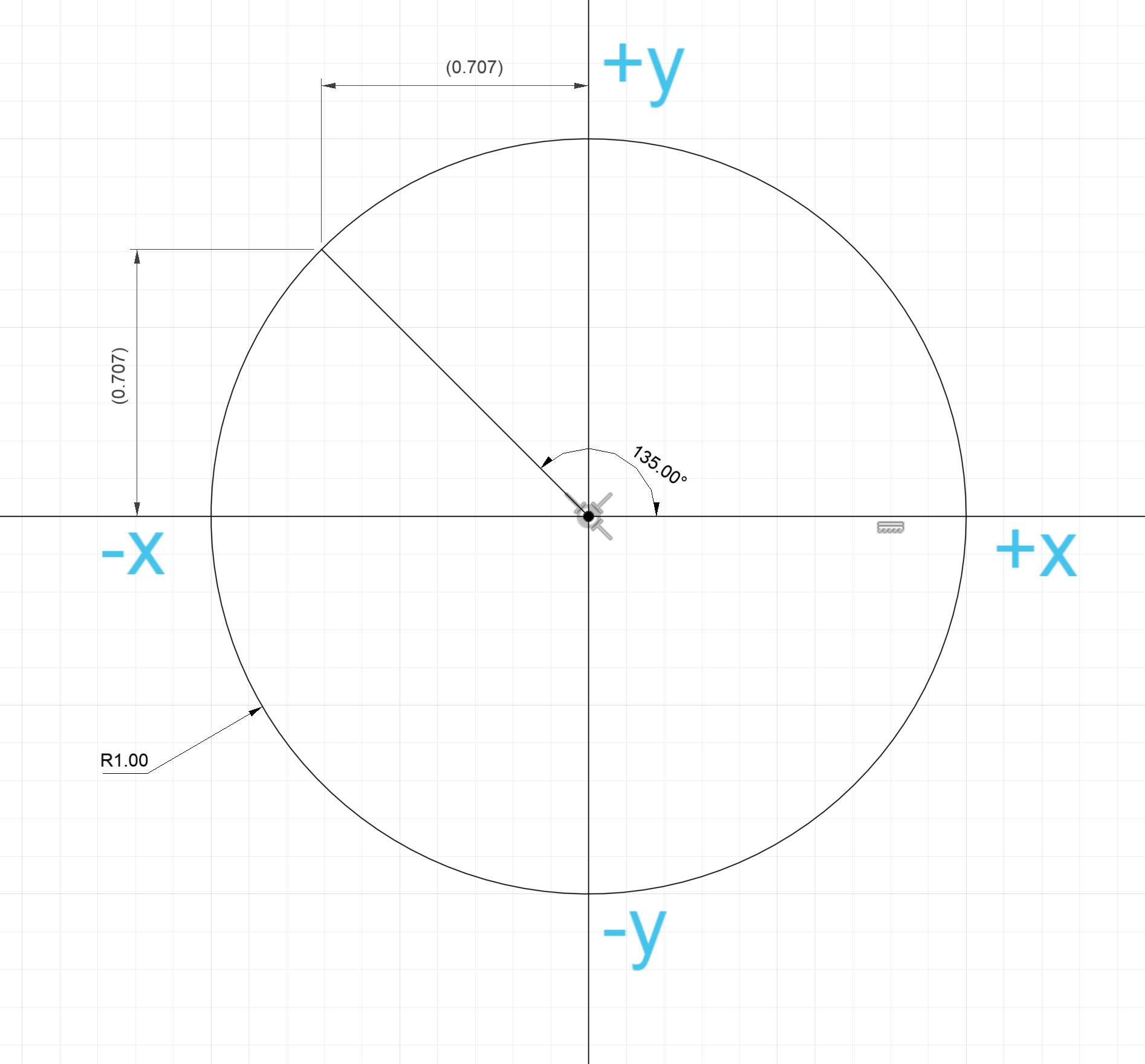
Figure 26: Extension of trigonometric functions to cover entire unit circle
Because the end point of the arc is located to the left of the y-axis, it's coordinates are $(-0.707,0.707)$. It has a negative $x$ coordinate. If we calculate the sine, cosine, and tangent as we did before for arcs, we obtain:
$sin(\theta) = y = 0.707$
$cos(\theta) = x = -0.707$
$tan(\theta) = \frac{y}{x} = -1$
Nothing stops us from segmenting the upper left quadrant further or even from continuing all the way around the circle to find a value for sine, cosine, and tangent for every angle around the unit circle.
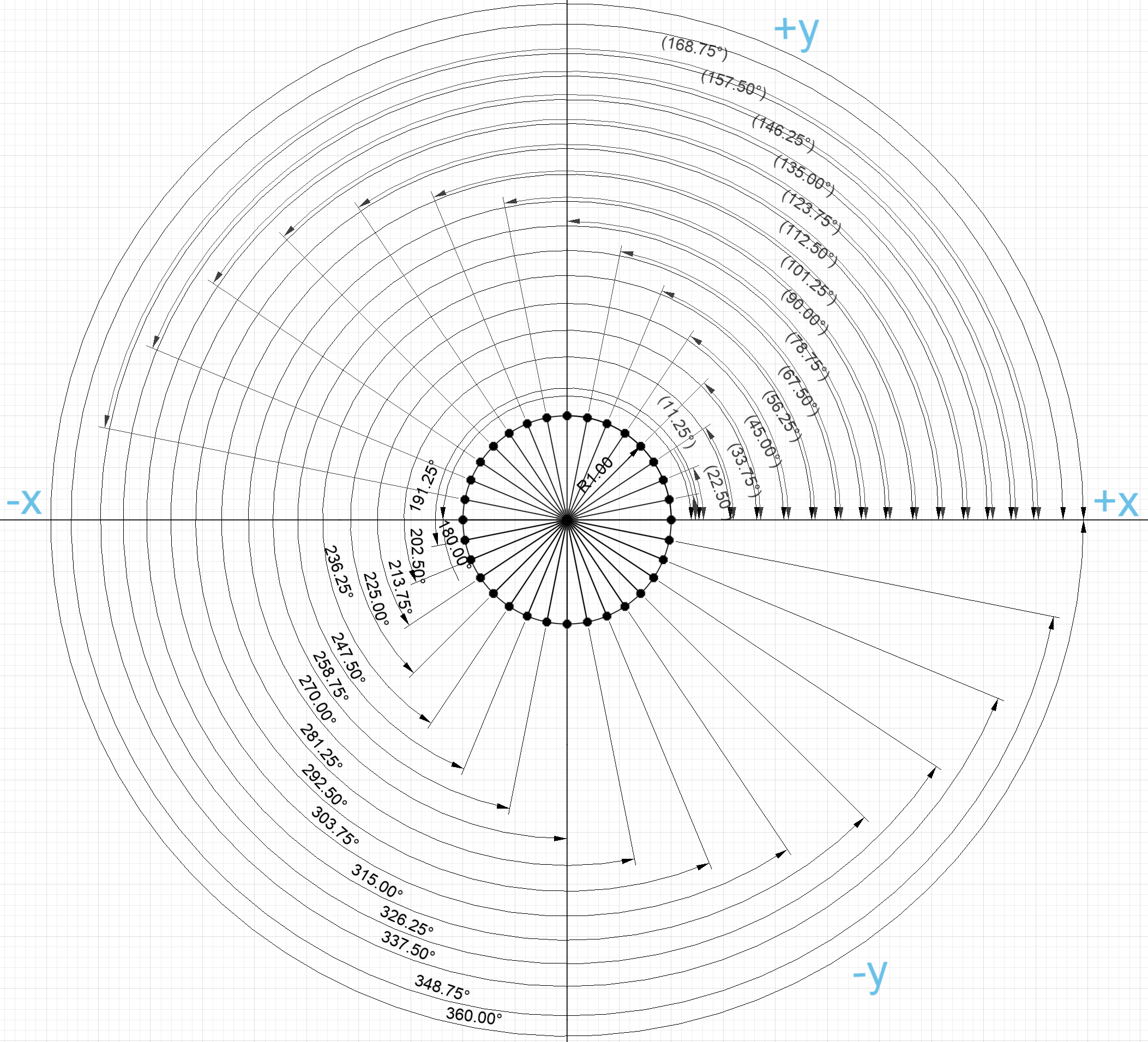
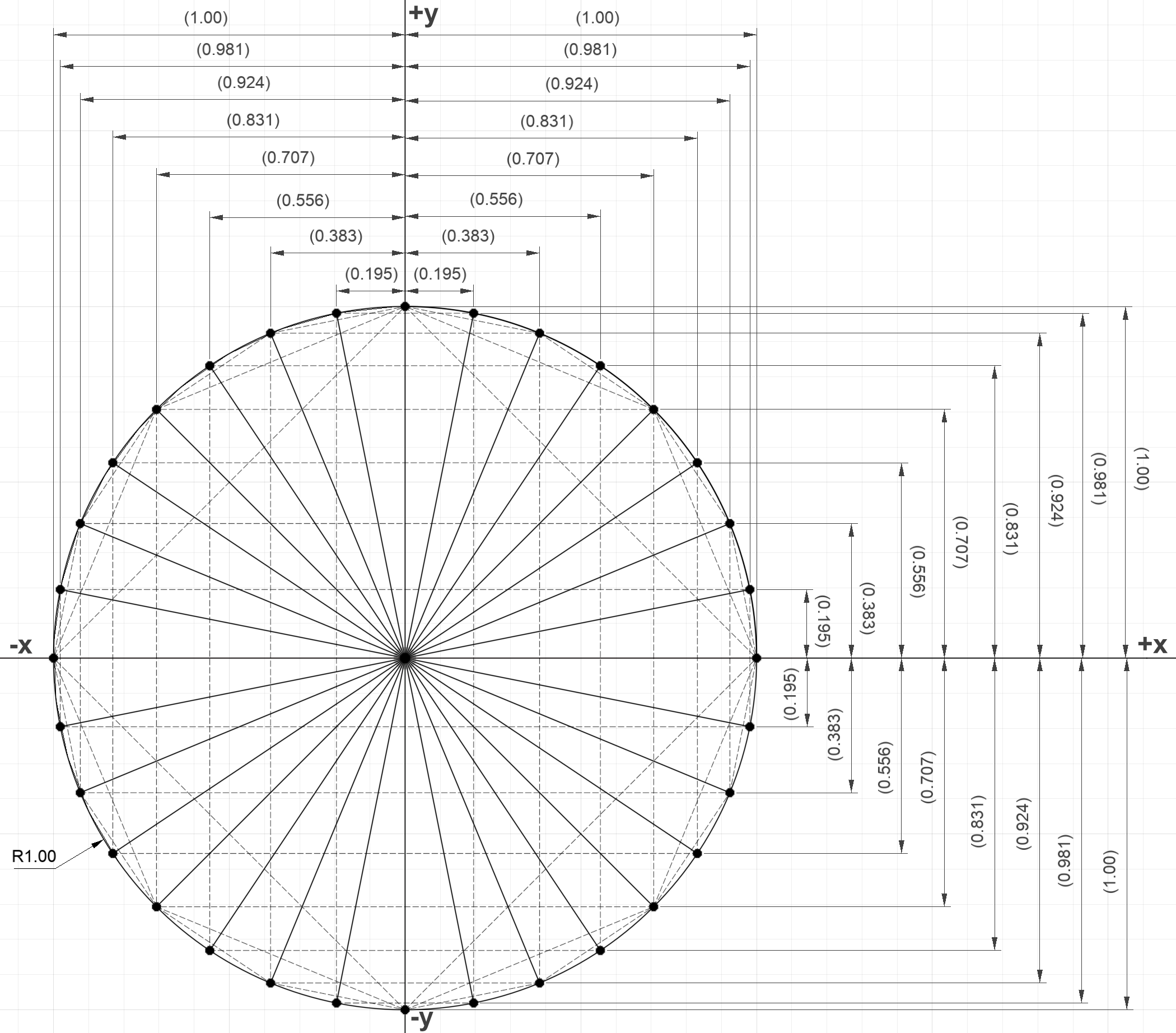
Figure 27: Segmentation of unit circle to determine trigonometric function values over entire circle.
The resulting trigonometric function table is below. It's starting to get long.
| Fraction of Circle | Angle (Degrees) | Angle (Radians) | Sine | Cosine | Tangent |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 1/32 | 11.25 | π/16 | 0.195 | 0.981 | 0.199 |
| 2/32 | 22.5 | π/8 | 0.383 | 0.924 | 0.415 |
| 3/32 | 33.75 | 3π/16 | 0.556 | 0.831 | 0.669 |
| 4/32 | 45 | π/4 | 0.707 | 0.707 | 1 |
| 5/32 | 56.25 | 5π/16 | 0.831 | 0.556 | 1.495 |
| 6/32 | 67.5 | 3π/8 | 0.924 | 0.383 | 2.413 |
| 7/32 | 78.75 | 7π/16 | 0.981 | 0.195 | 5.031 |
| 8/32 | 90 | π/2 | 1 | 0 | Undefined |
| 9/32 | 101.25 | 9π/16 | 0.981 | -0.195 | -5.031 |
| 10/32 | 112.5 | 5π/8 | 0.924 | -0.383 | -2.413 |
| 11/32 | 123.75 | 11π/16 | 0.831 | -0.556 | -1.495 |
| 12/32 | 135 | 3π/4 | 0.707 | -0.707 | -1 |
| 13/32 | 146.25 | 13π/16 | 0.556 | -0.831 | -0.669 |
| 14/32 | 157.5 | 7π/8 | 0.383 | -0.924 | -0.415 |
| 15/32 | 168.75 | 15π/16 | 0.195 | -0.981 | -0.199 |
| 16/32 | 180 | π | 0 | -1 | 0 |
| 17/32 | 191.25 | 17π/16 | -0.195 | -0.981 | 0.199 |
| 18/32 | 202.5 | 9π/8 | -0.383 | -0.924 | 0.415 |
| 19/32 | 213.75 | 19π/16 | -0.556 | -0.831 | 0.669 |
| 20/32 | 225 | 5π/4 | -0.707 | -0.707 | 1 |
| 21/32 | 236.25 | 21π/16 | -0.831 | -0.556 | 1.495 |
| 22/32 | 247.5 | 11π/8 | -0.924 | -0.383 | 2.413 |
| 23/32 | 258.75 | 23π/16 | -0.981 | -0.195 | 5.031 |
| 24/32 | 270 | 12π/8 | -1 | 0 | Undefined |
| 25/32 | 281.25 | 25π/16 | -0.981 | 0.195 | -5.031 |
| 26/32 | 292.5 | 13π/8 | -0.924 | 0.383 | -2.413 |
| 27/32 | 303.75 | 27π/16 | -0.831 | 0.556 | -1.495 |
| 28/32 | 315 | 14π/8 | -0.707 | 0.707 | -1 |
| 29/32 | 326.25 | 29π/16 | -0.556 | 0.831 | -0.669 |
| 30/32 | 337.5 | 15π/8 | -0.383 | 0.924 | -0.415 |
| 31/32 | 348.75 | 31π/16 | -0.195 | 0.981 | -0.199 |
| 32/32 | 360 | 2π | 0 | 1 | 0 |
Let's graph these functions.
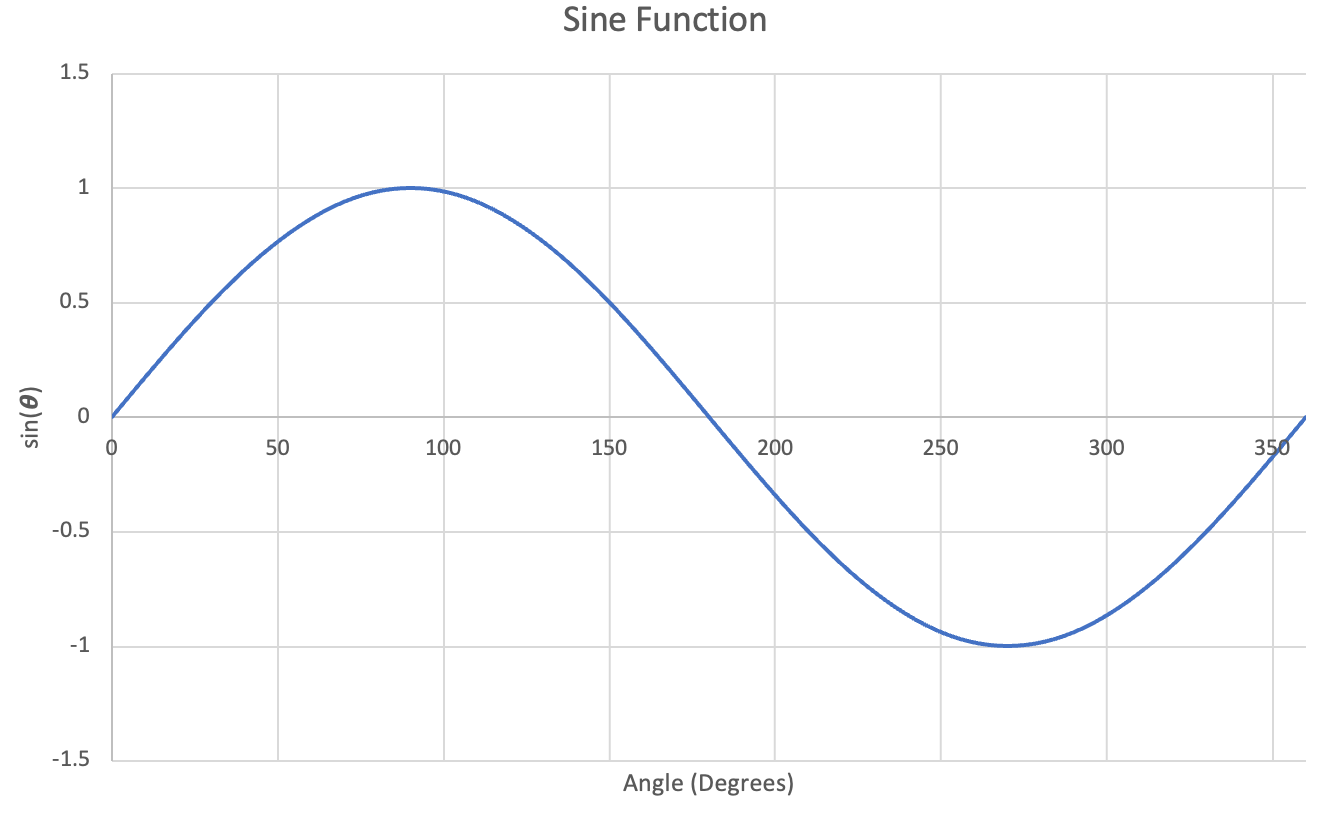
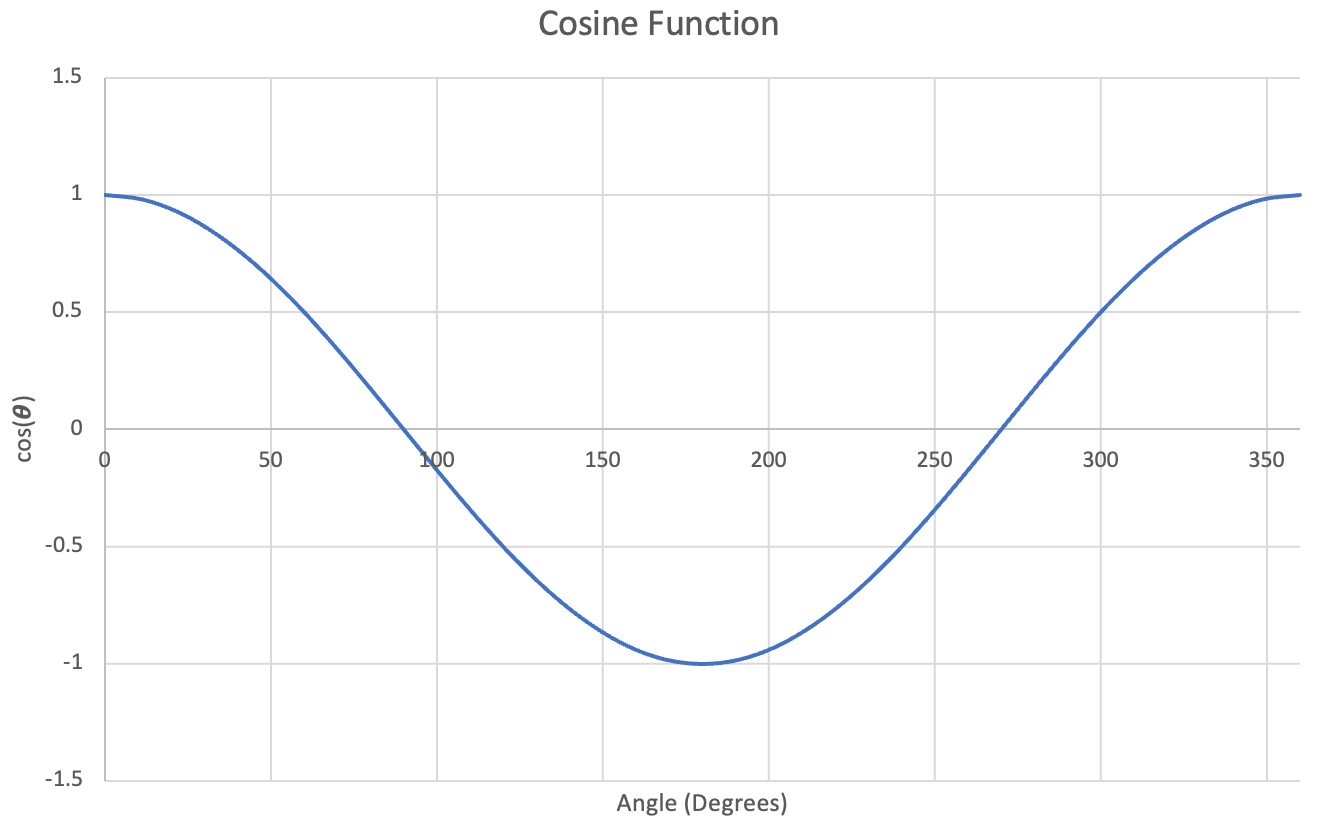
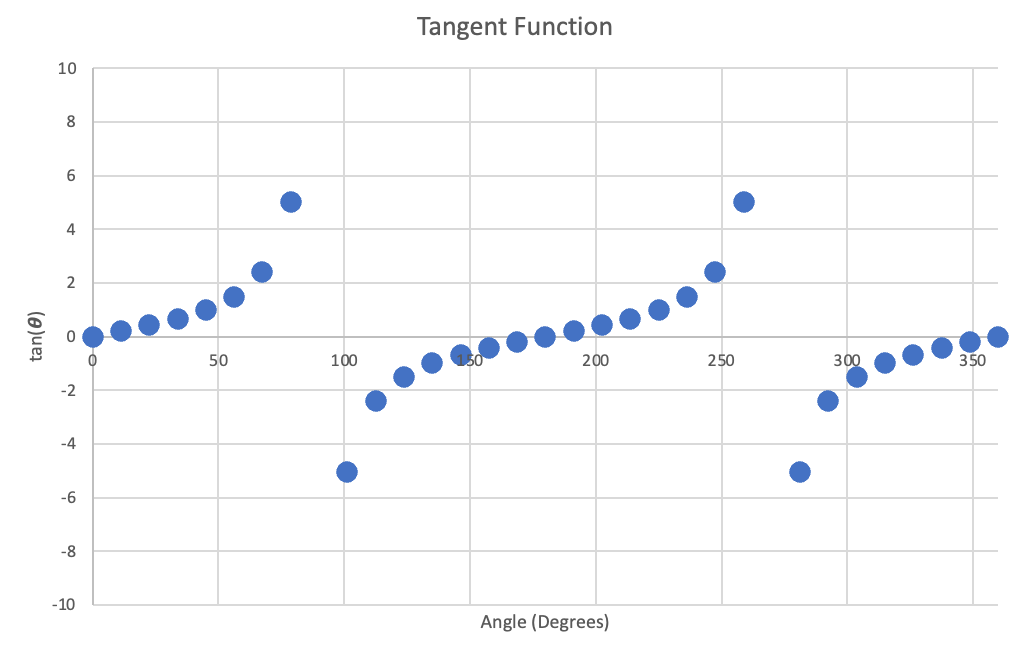
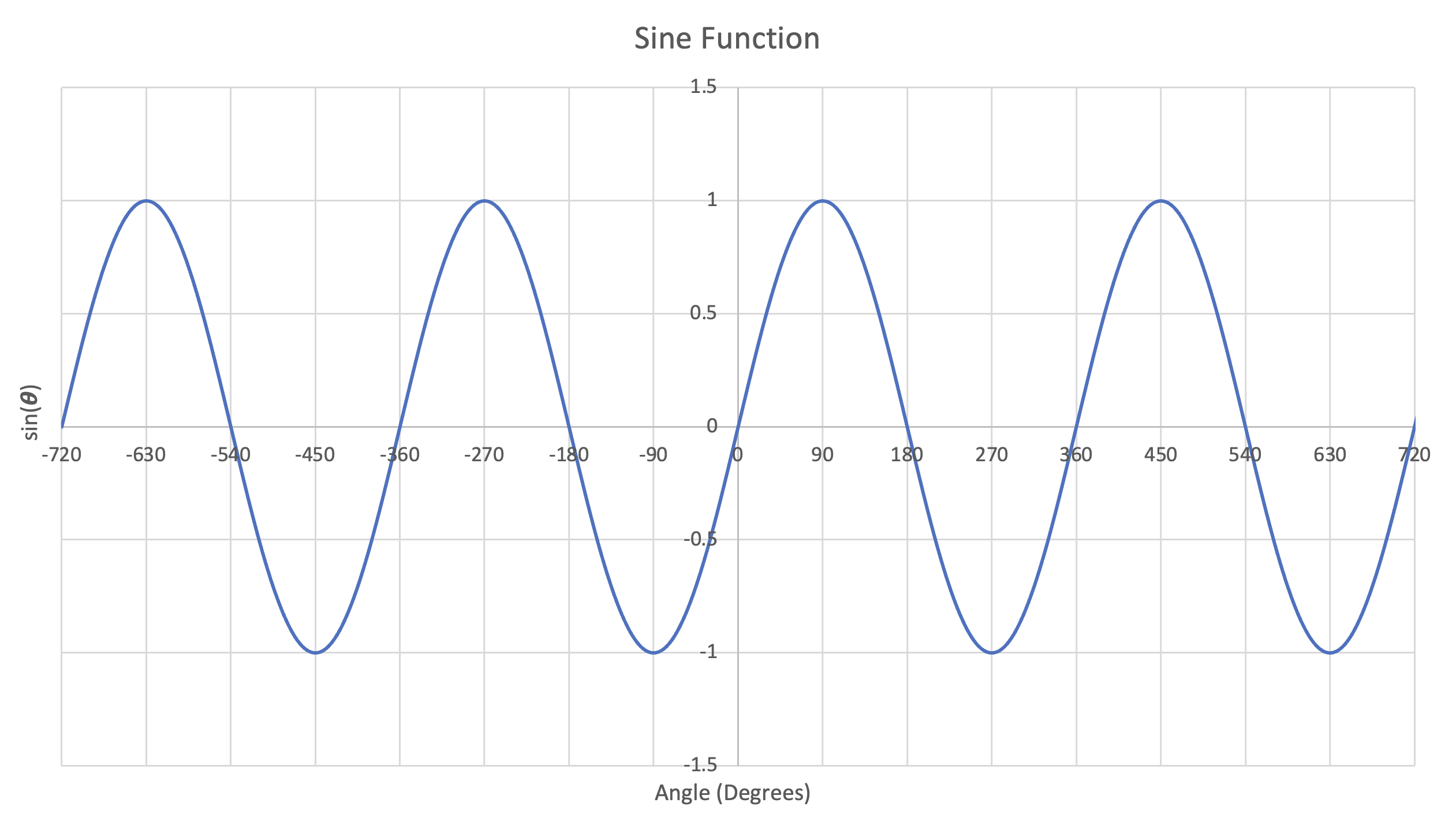
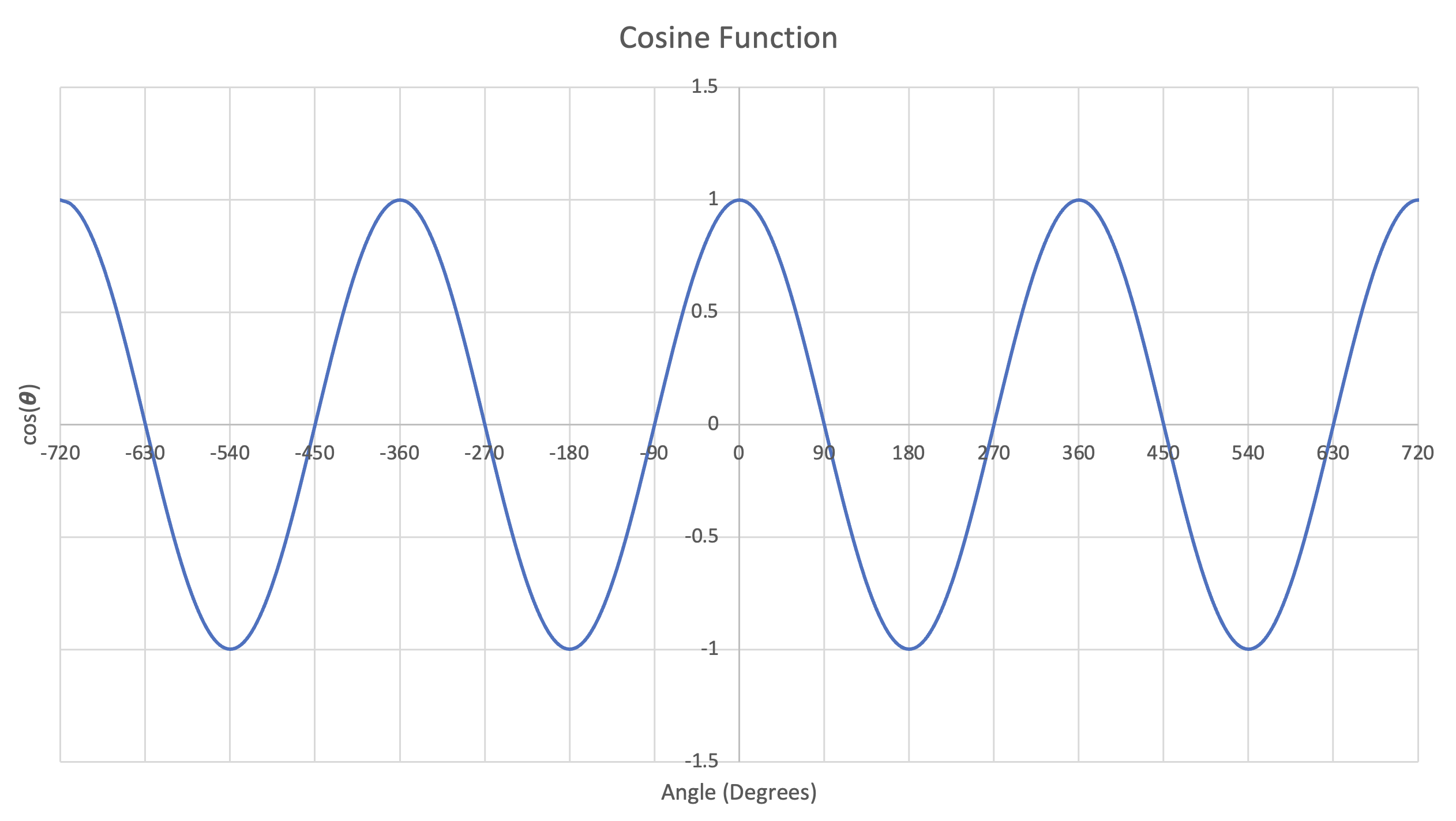
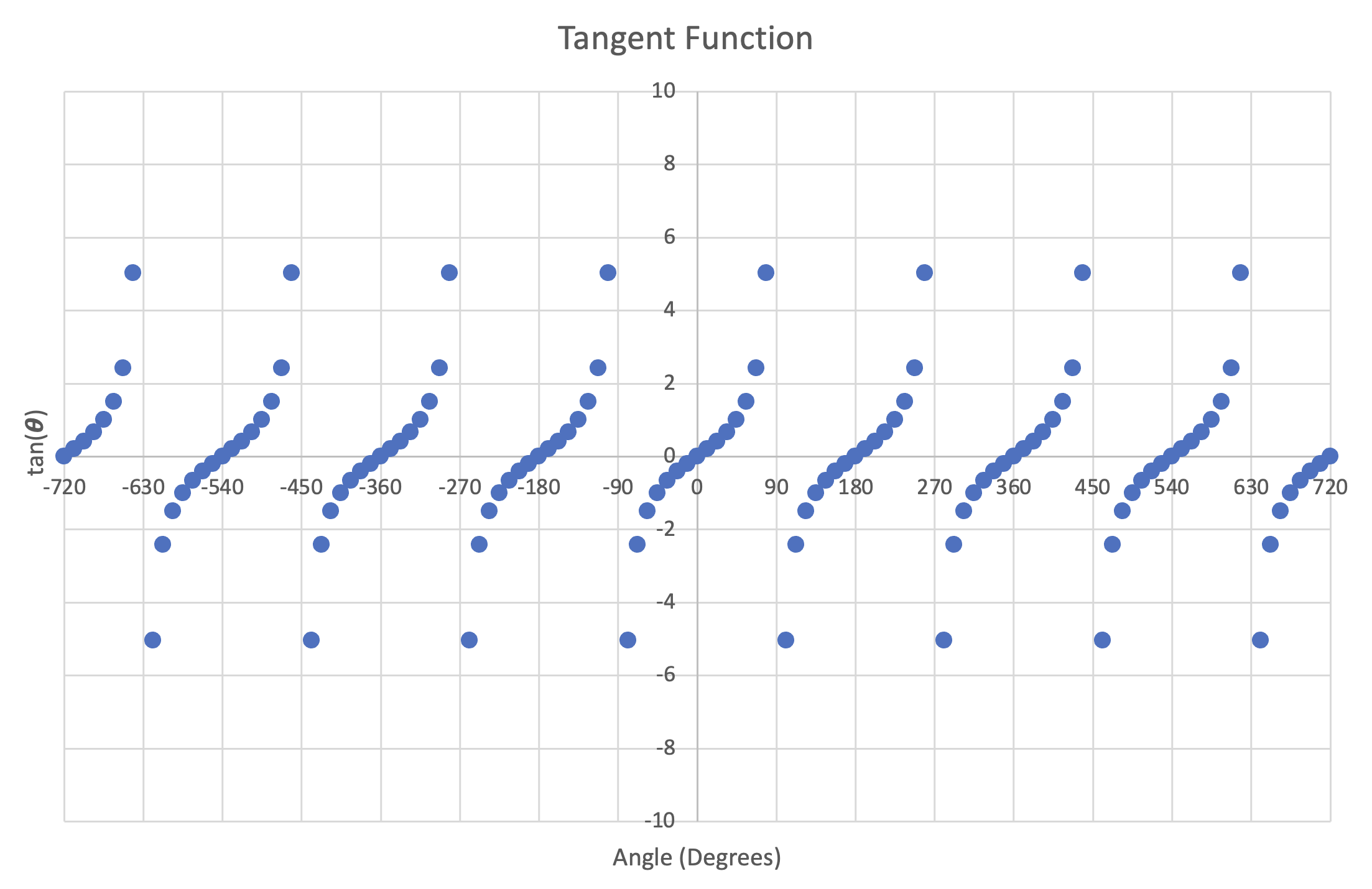
Figure 28: Left- Plot of Sine function, $0^\circ-360^\circ$ | Center- Plot of Cosine function, $0^\circ-360^\circ$ | Right- Plot of Tangent function, $0^\circ-360^\circ$
Dots were used for the tangent function instead of lines to better depict its behavior.
Note that because we've obtained values over a full revolution, $360^\circ$, the functions repeat for negative and positive angles (continuing around the circle). This means that we can now evaluate the sine, cosine and tangent functions for any possible input number (with the small exception that the tangent function is still undefined at exactly $n(90^\circ)$ and $n(270^\circ)$ where $n$ is any integer).
Inverse Trigonometric Functions
Unfortunately, the inverse trigonometric functions do not extend well to the full circle or repeat. If we simply invert the trigonometric functions (as before) and plot them, we obtain the following:
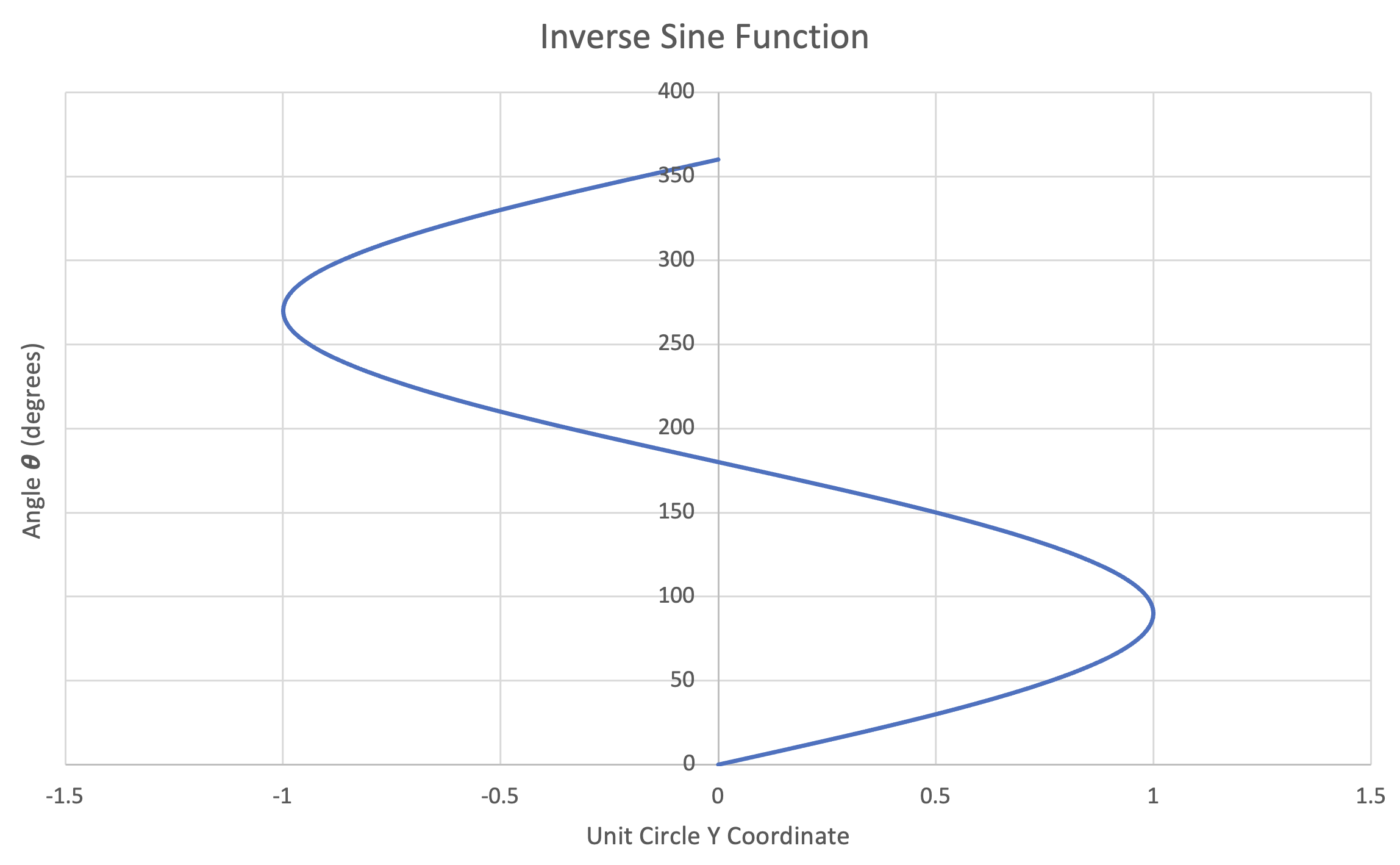
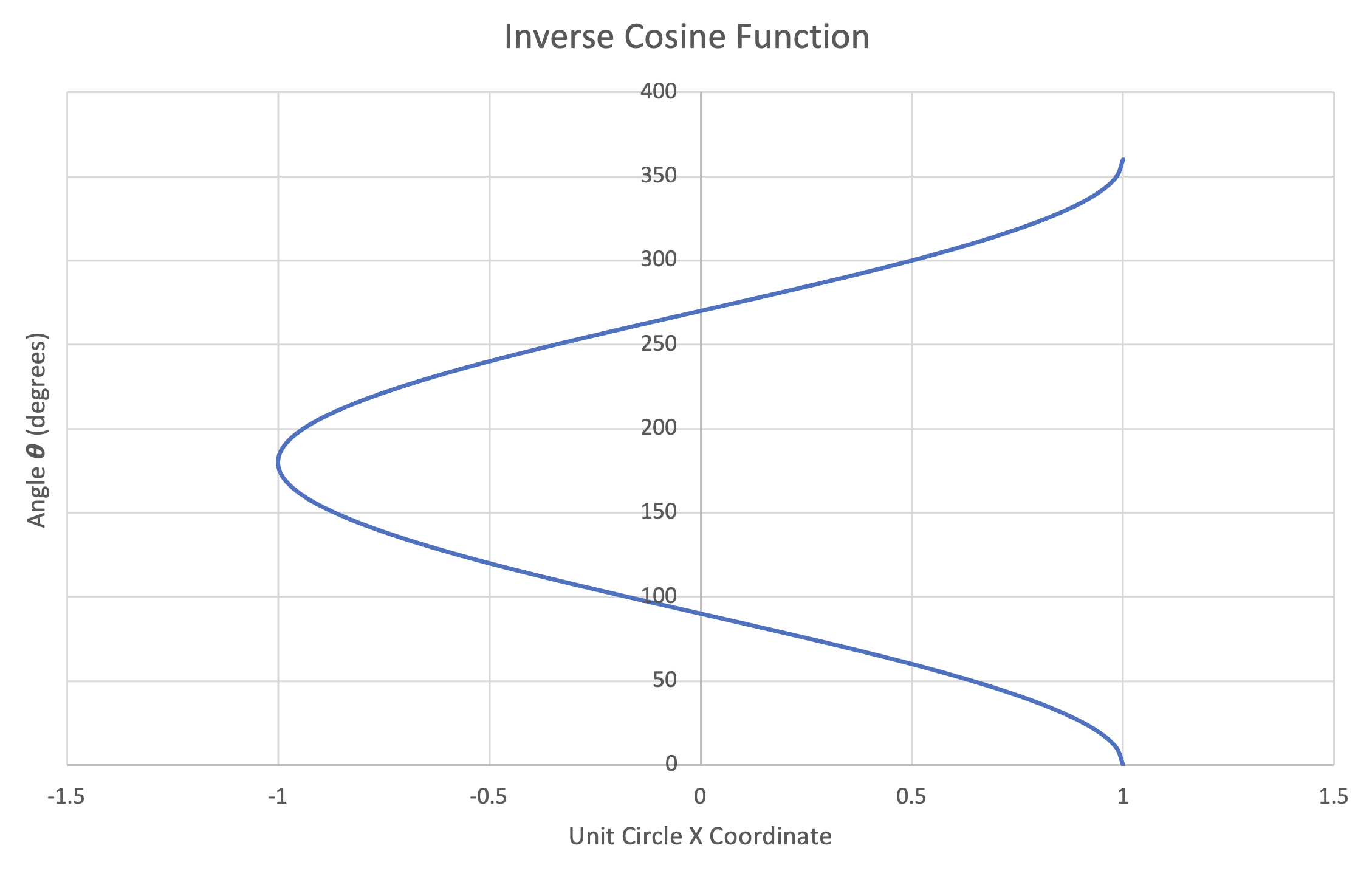
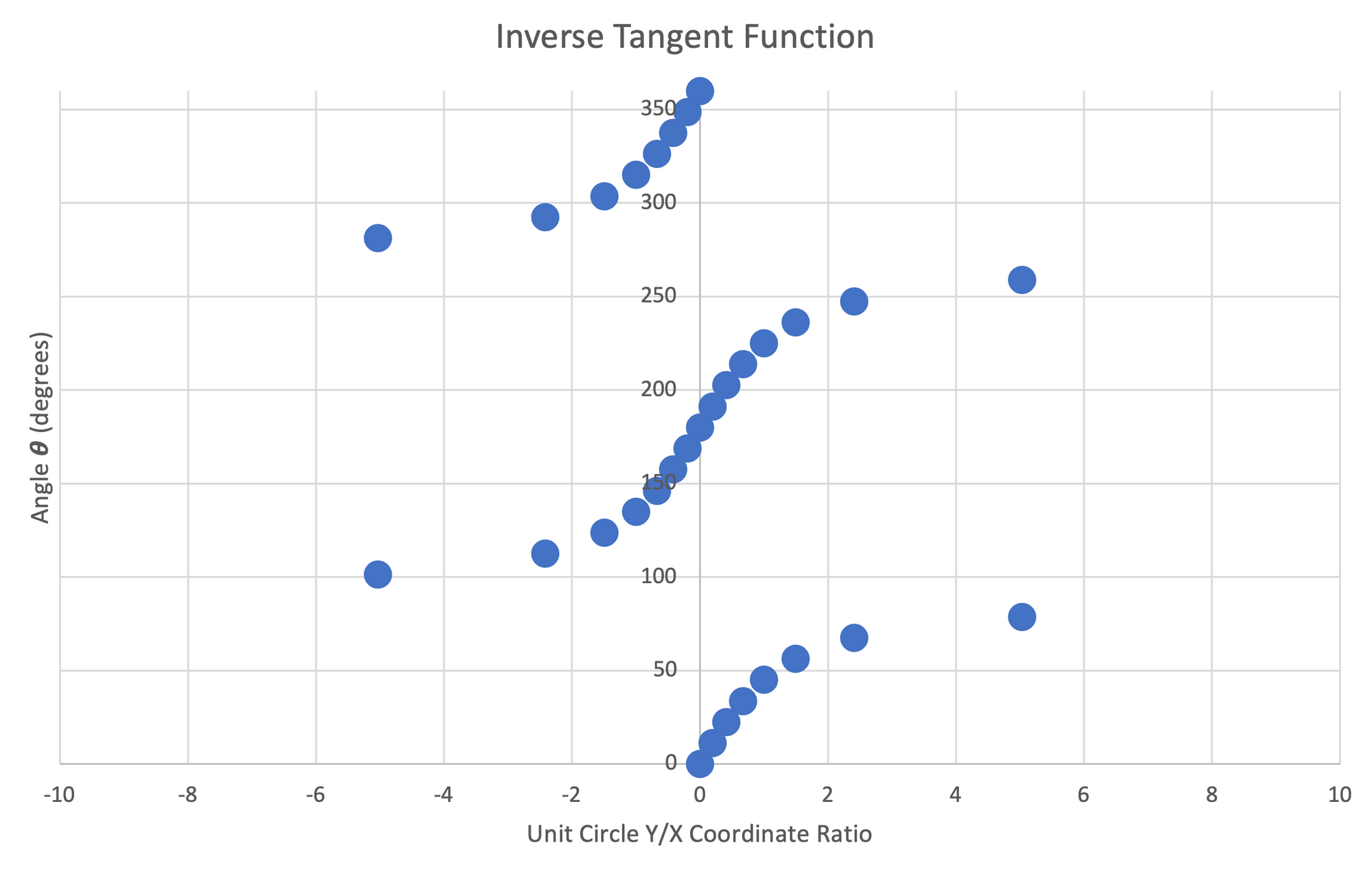
Figure 28: Left- Plot of Inverse Sine function, $0^\circ-360^\circ$ | Center- Plot of Inverse Cosine function, $0^\circ-360^\circ$ | Right- Plot of Inverse Tangent function, $0^\circ-360^\circ$
In order for a mathematical function to actually be a function, each input $x$ can only have one output $y$. From the above plots, we can see that every input value $x$ has multiple outputs $y$. Therefore, for each trigonometric function, we must predefine the single output $y$ for any given input $x$.
For $sin^{-1}$, the permissible output range is from $-90^\circ$ to $90^\circ$.
For $cos^{-1}$, the permissible output range is from $0^\circ$ to $180^\circ$.
For $tan^{-1}$, the permissible output range is from $-90^\circ$ to $90^\circ$.
With these definitions, our inverse trigonometric functions are now actually functions.
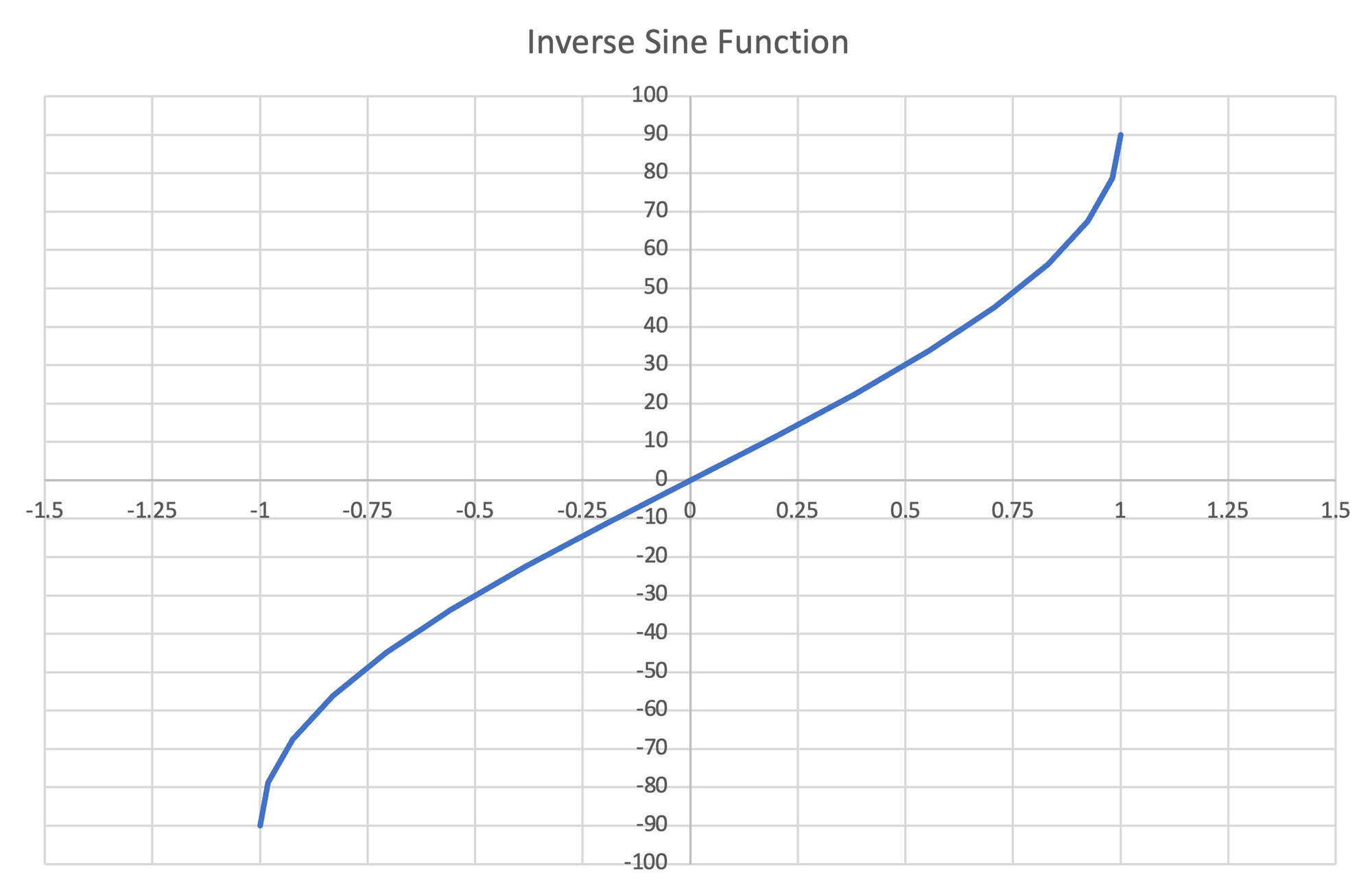
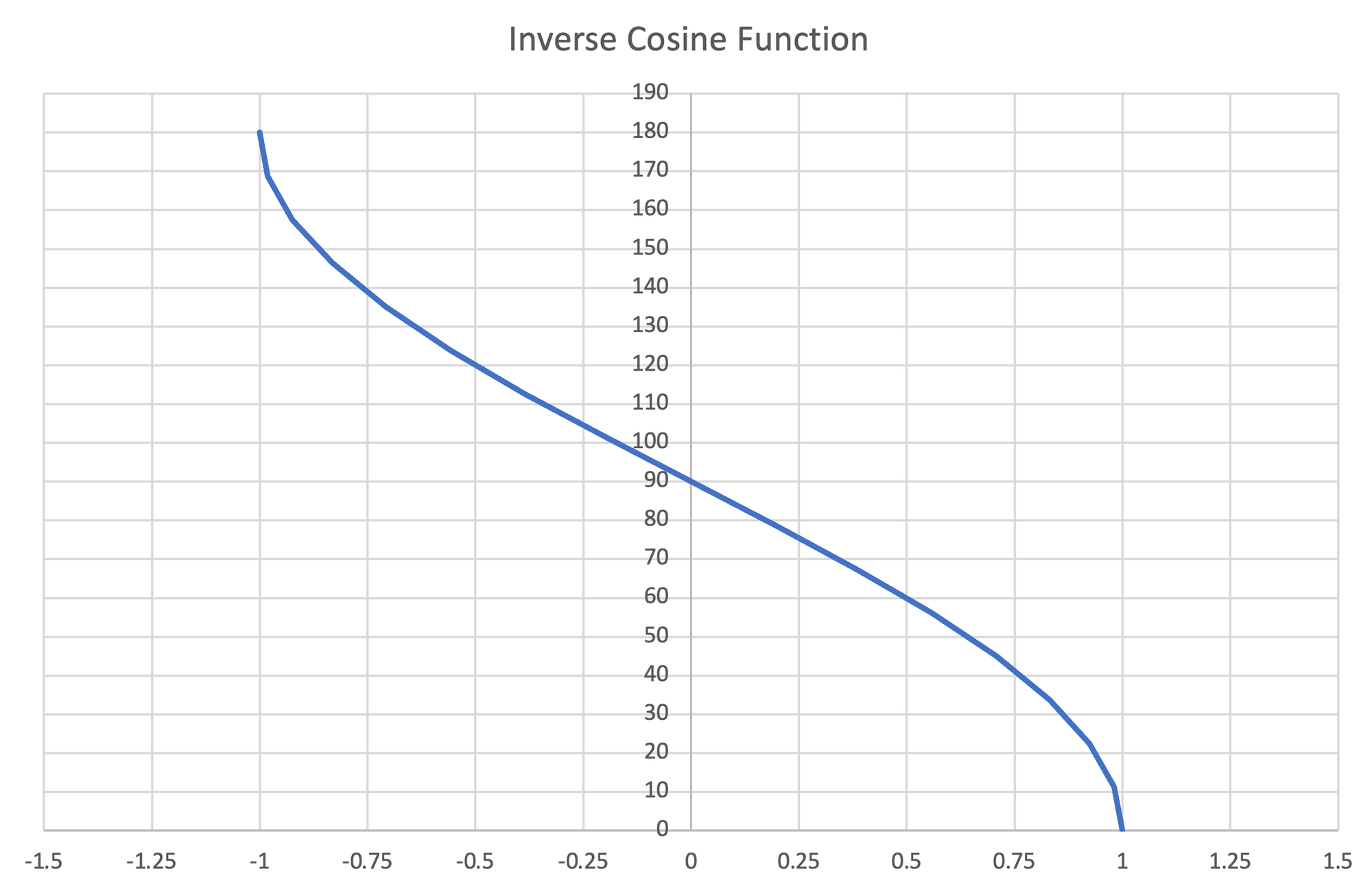
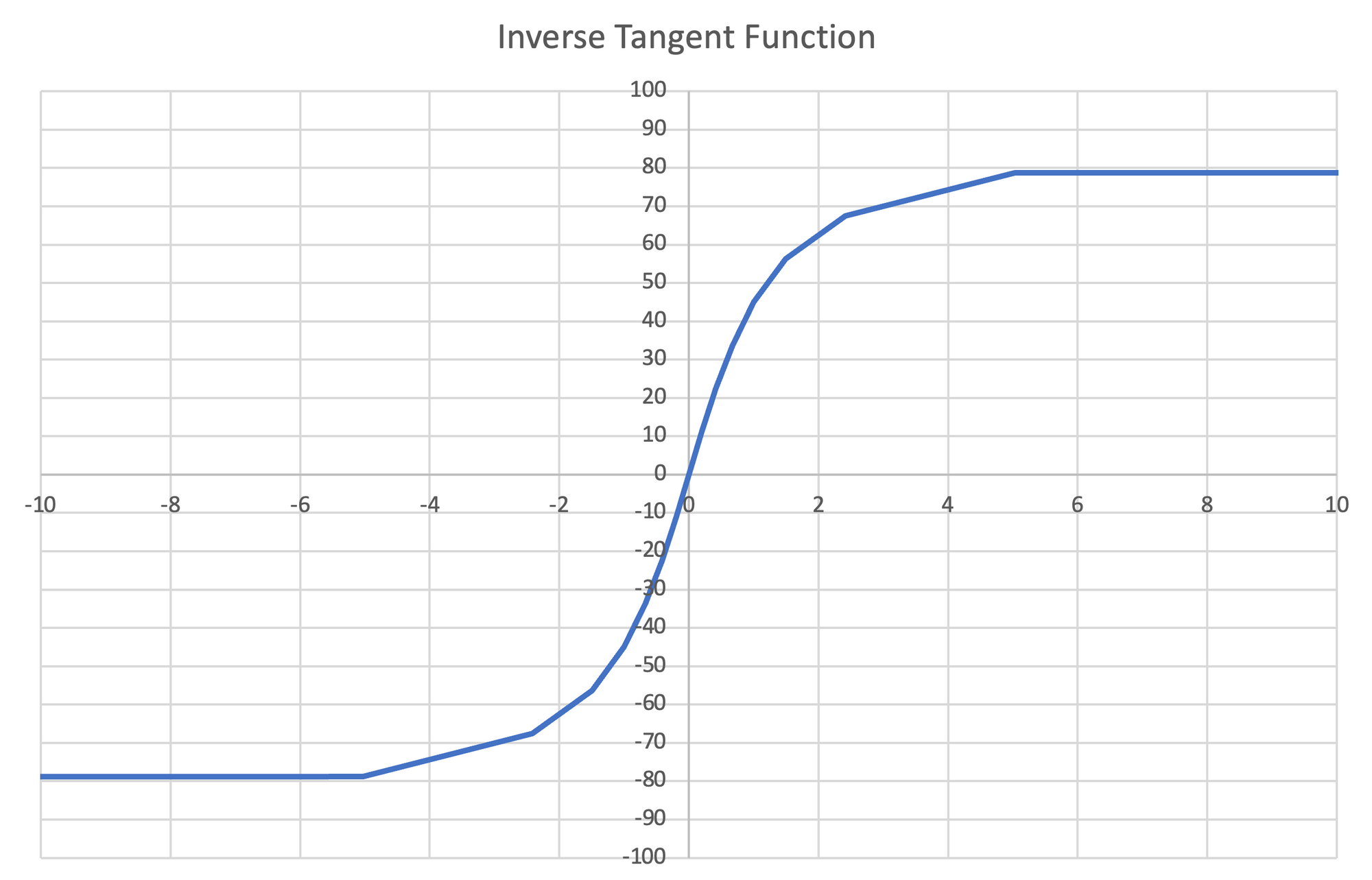
Figure 29: Left- Plot of Inverse Sine function, $-90^\circ-90^\circ$ | Center- Plot of Inverse Cosine function, $0^\circ-180^\circ$ | Right- Plot of Inverse Tangent function, $-90^\circ-90^\circ$
Because the inverse cosine function works over a larger positive angle range than the inverse sine or inverse tangent functions, it is more commonly used. The inverse tangent function is interesting because as a ratio, it is applicable for all inputs (the inverse sine and inverse cosine functions are only valid for inputs between $-1$ and $1$ corresponding to the unit circle).
Four Quadrant Inverse Tangent
One purpose of the inverse trigonometric functions was to determine the angle that corresponds to a radius $1$ unit circle's coordinates $x$, $y$, or the ratio $\frac{y}{x}$. An advantage of the inverse tangent function is that because it is a ratio of coordinates, it is valid for any input, even those not on the unit circle. One drawback of the inverse tangent function is it's only capable of outputting an angle between $-90^\circ$ to $90^\circ$. To resolve this issue, we invented the four quadrant inverse tangent, also called the two argument inverse arctangent.
The two argument inverse arctangent takes in a position ($x$,$y$) and outputs the angle between the $x$ axis and the line from the origin to the coordinates.
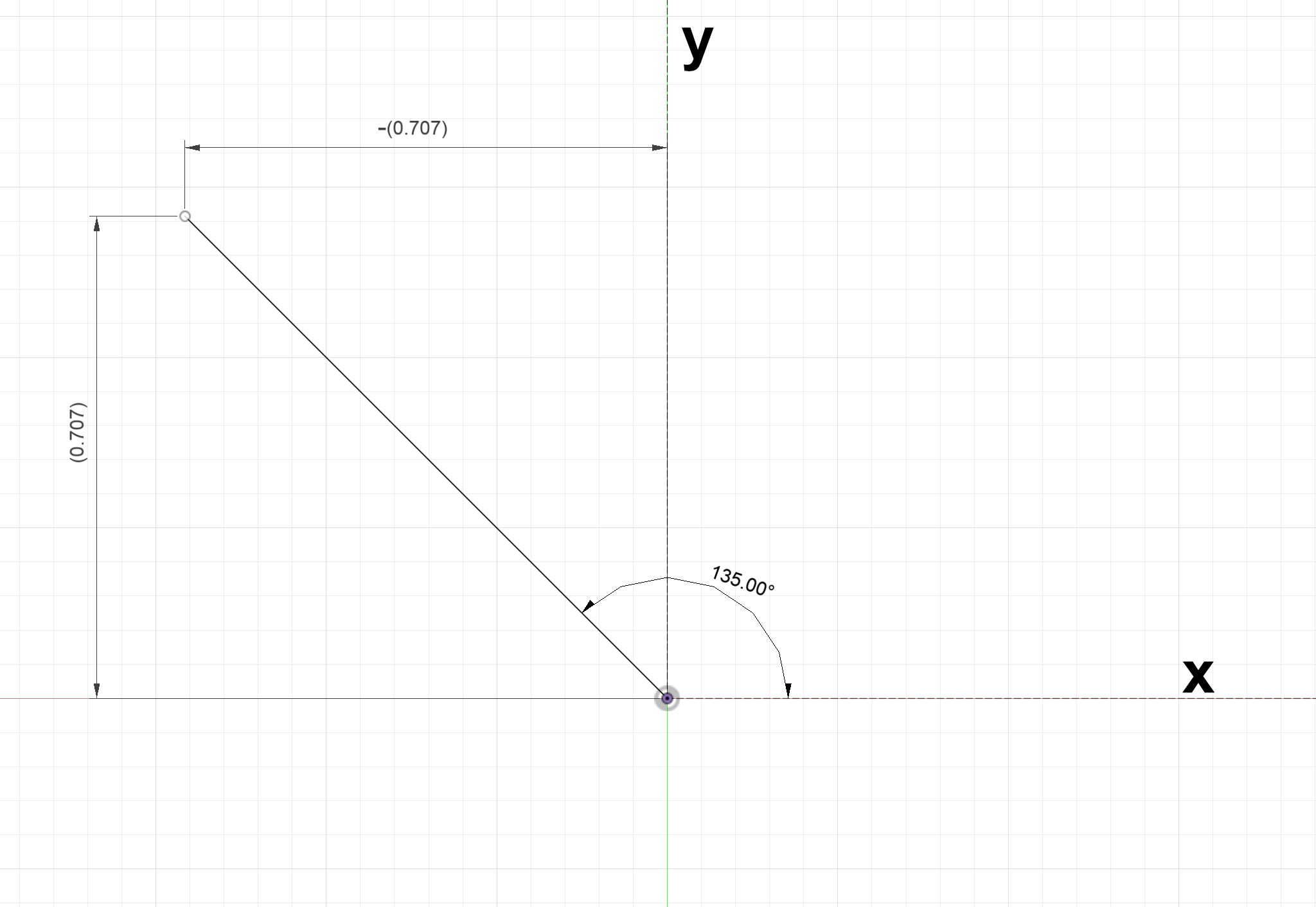
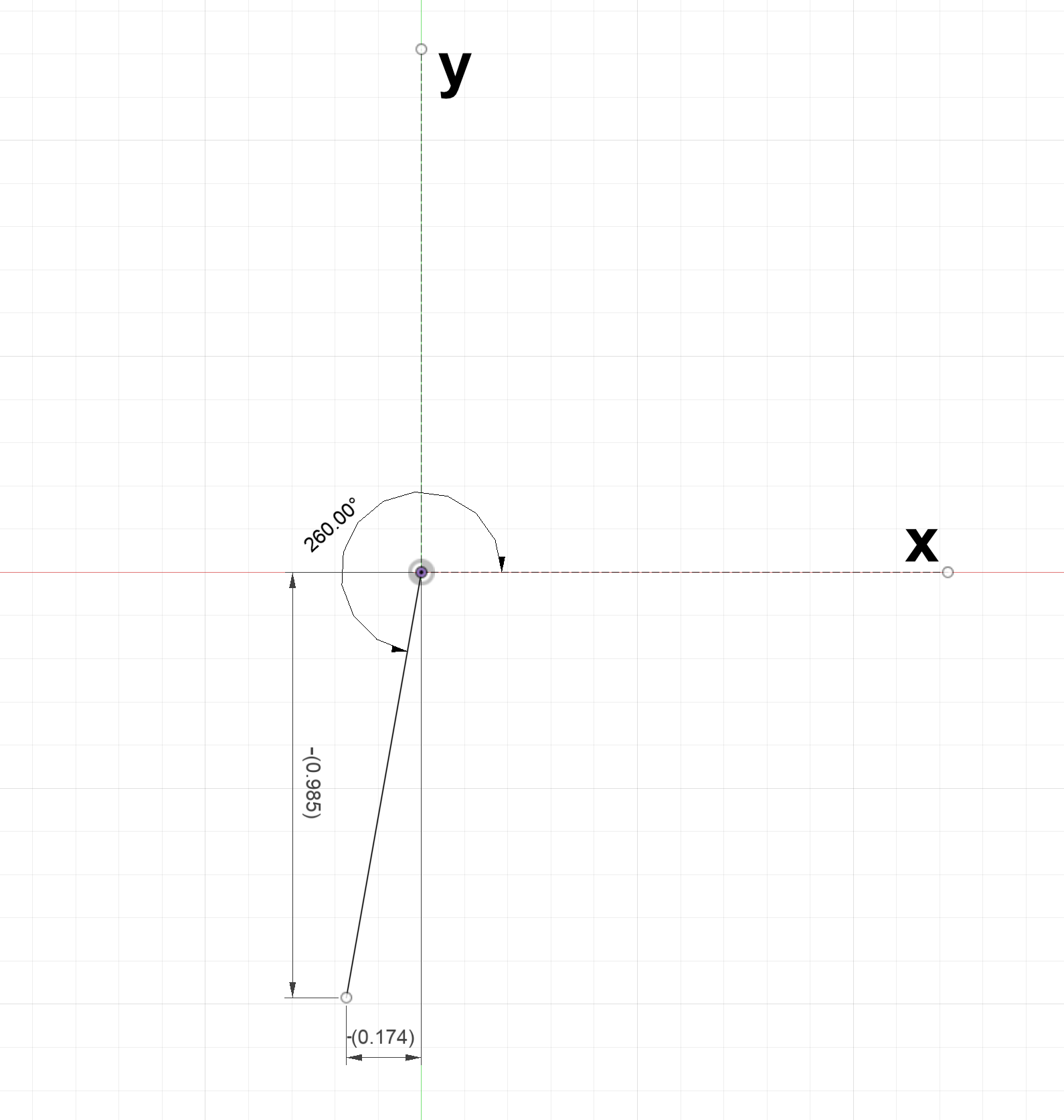
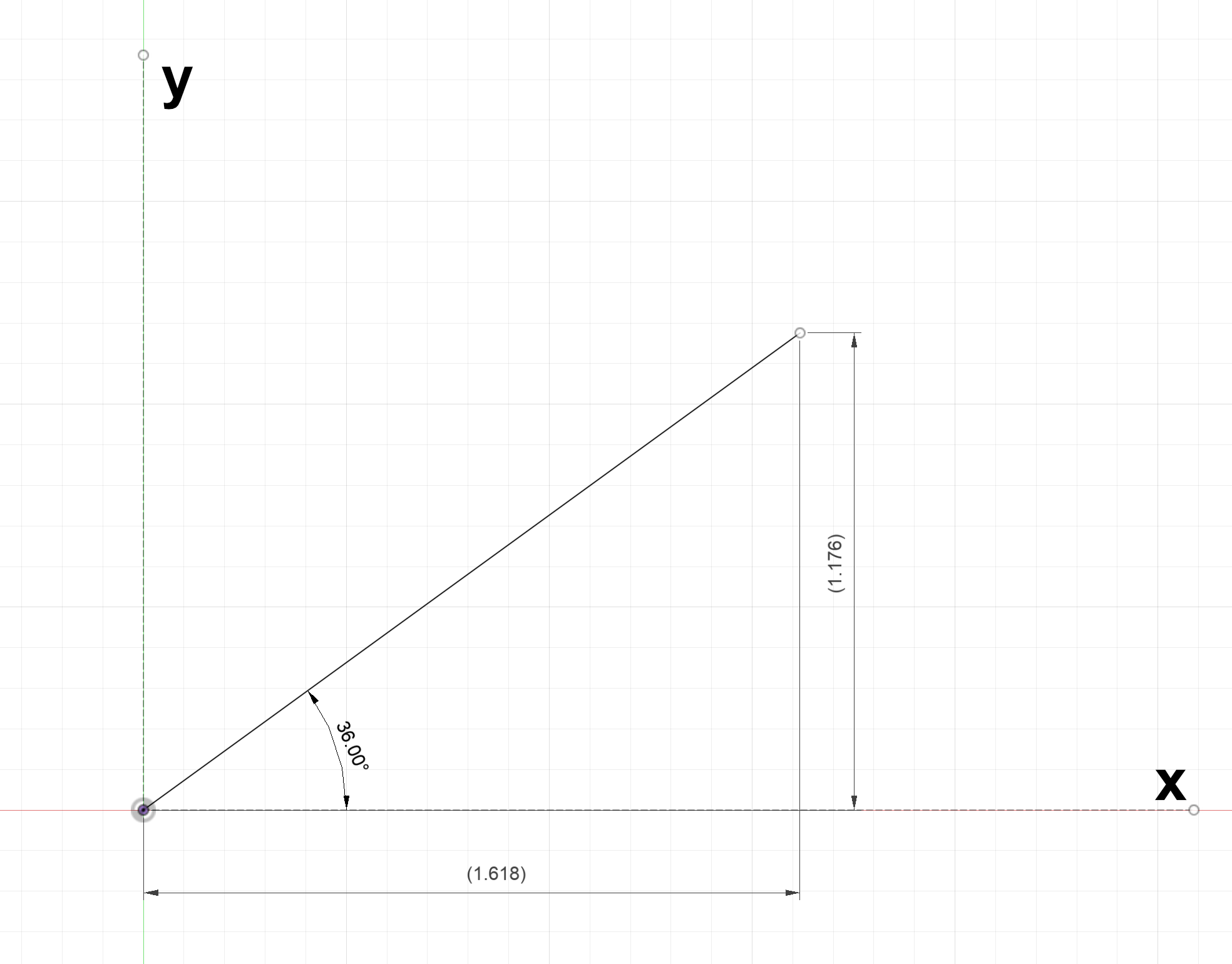
Figure 30: Three examples for applying the four quadrant inverse arctangent
The four quadrant inverse tangents of the coordinates shown above, in order, are:
$atan2(-0.707,0.707) = 135^\circ$
$atan2(-0.174,-0.985) = 260^\circ$
$atan2(1.618,1.176) = 36^\circ$
The function uses the sign of the input $x$ to determine whether the angle is between $-90^\circ$ and $90^\circ$ (positive $x$) or between $90^\circ$ and $270^\circ$ (negative $x$). The four quadrant inverse tangent function is given by:
$atan2(x,y) = \begin{cases} tan^{-1}(\frac{y}{x}),\: \text{if}\:x > 0 \\ tan^{-1}(\frac{y}{x}) + 180^\circ,\: \text{if}\: x < 0\:\&\:y \ge 0 \\ tan^{-1}(\frac{y}{x}) - 180^\circ,\: \text{if}\: x < 0\:\& y\:< 0\\ 90^\circ,\: \text{if}\: x = 0\: \& \:y > 0 \\ -90^\circ,\: \text{if}\: x = 0\: \& \:y < 0 \\ \text{undefined},\: \text{if}\: x = 0\:\&\:y=0\end{cases}$
This is a function of two inputs with one output.
Reciprocal Trigonometric Functions: Cosecant, Secant, and Cotangent
Cosecant (csc), secant (sec) , and cotangent (cot), are simply the reciprocal of the sine (sin), cosine (cos), and tangent (tan) functions:
$cosecant = csc = \frac{1}{sin}$
$secant = sec = \frac{1}{cos}$
$cotangent = cot = \frac{1}{tan}$
If you are deeply annoyed that cosecant is the reciprocal of sine instead of cosine... welcome to the club.
Hyperbolic Functions: Sinh, Cosh, Tanh
You might at some pint see the hyperbolic sine (sinh), hyperbolic cosine (cosh), and hyperbolic tangent (tanh) functions. Given their names, you might be inclined to believe they are related to the trigonometric functions but they are not.
The hyperbolic functions are vaguely related insofar as a similar exercise is used to create them but using a hyperbola instead of a circle. Generally, these functions are so disconnected from standard trigonometric functions that they should be thought of as distinct and unrelated to trigonometric functions.
Using Trigonometric Functions in Calculators
The exercise of generating the trigonometric functions from scratch is not actually necessary. We've done so here using very rudimentary techniques, but most just use calculators that other people have already created. One important thing to remember is that we always need to tell what units are angles are (radians or degrees). This is an easy but costly mistake to make.
Figure 31: Highlighted trigonometric functions Left- HP Prime | Center- macOS calculator app | Right- Microsoft Excel
The below examples demonstrate using trigonometric functions in calculators.
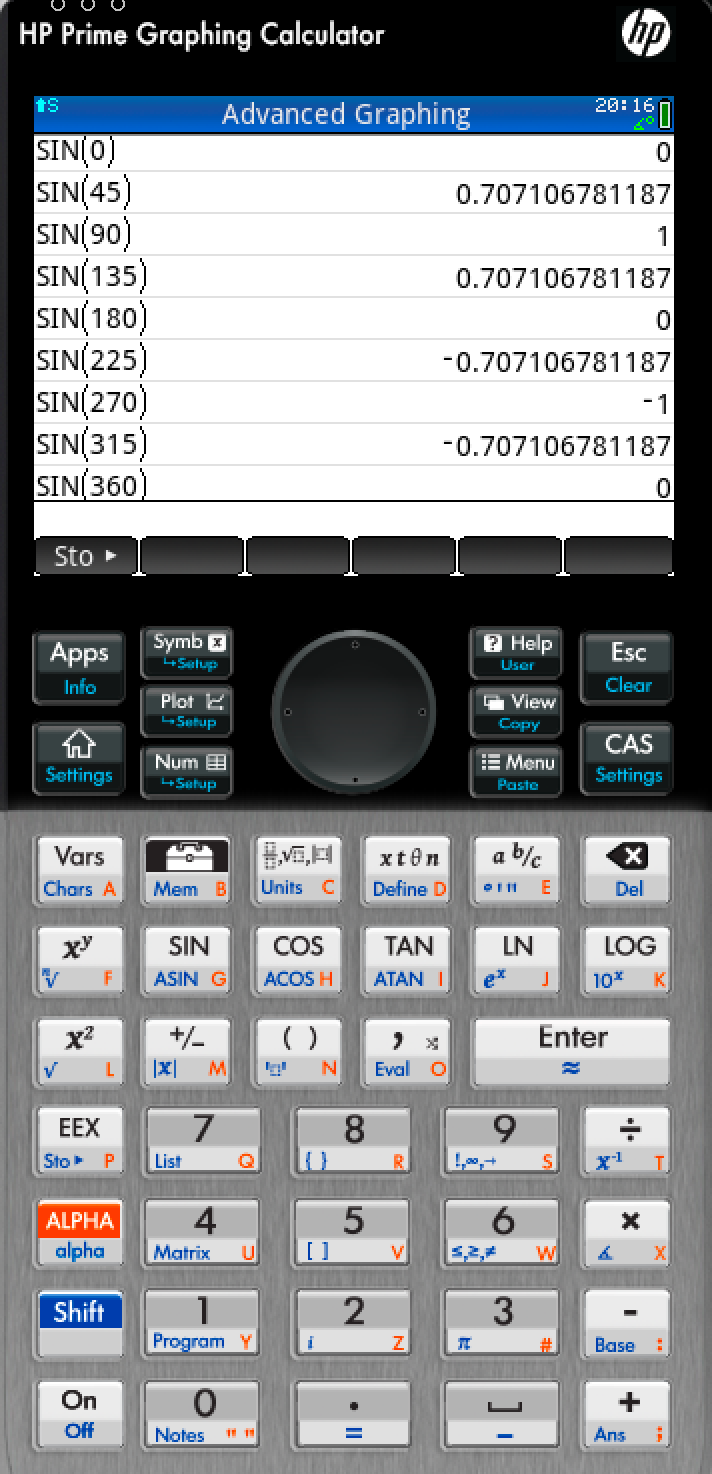
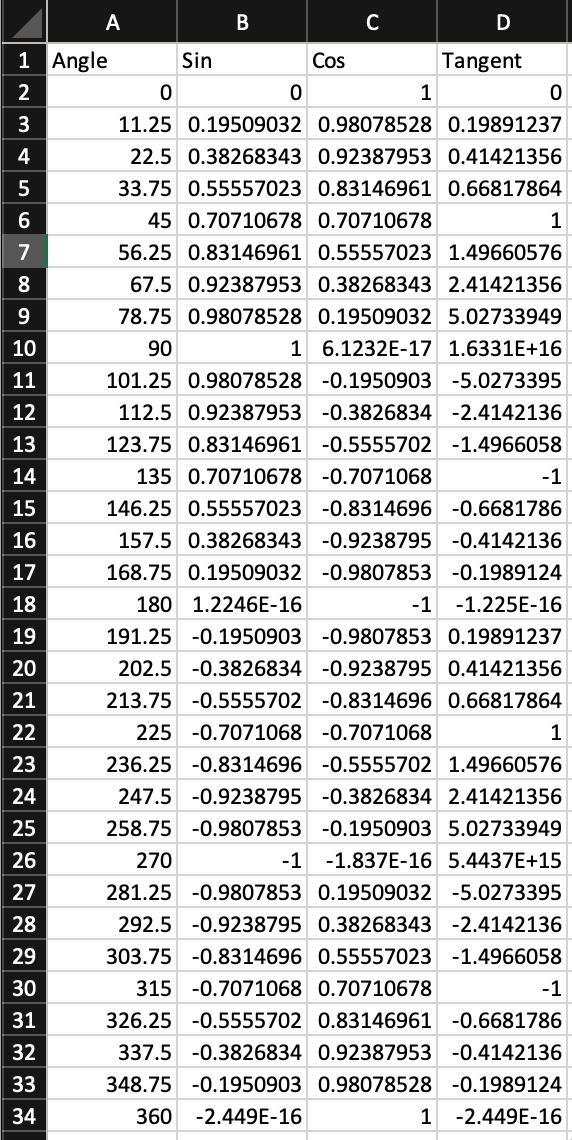
Figure 32: Demonstration of trigonometric function usage in calculators Left- HP Prime | Right- Microsoft Excel
Practical Applications of Trigonometric Functions
Splitting Angled Line into $x$ and $y$ Components
Suppose we have a line $L$ with length $6$ oriented $30^\circ$ from the $x$ axis.
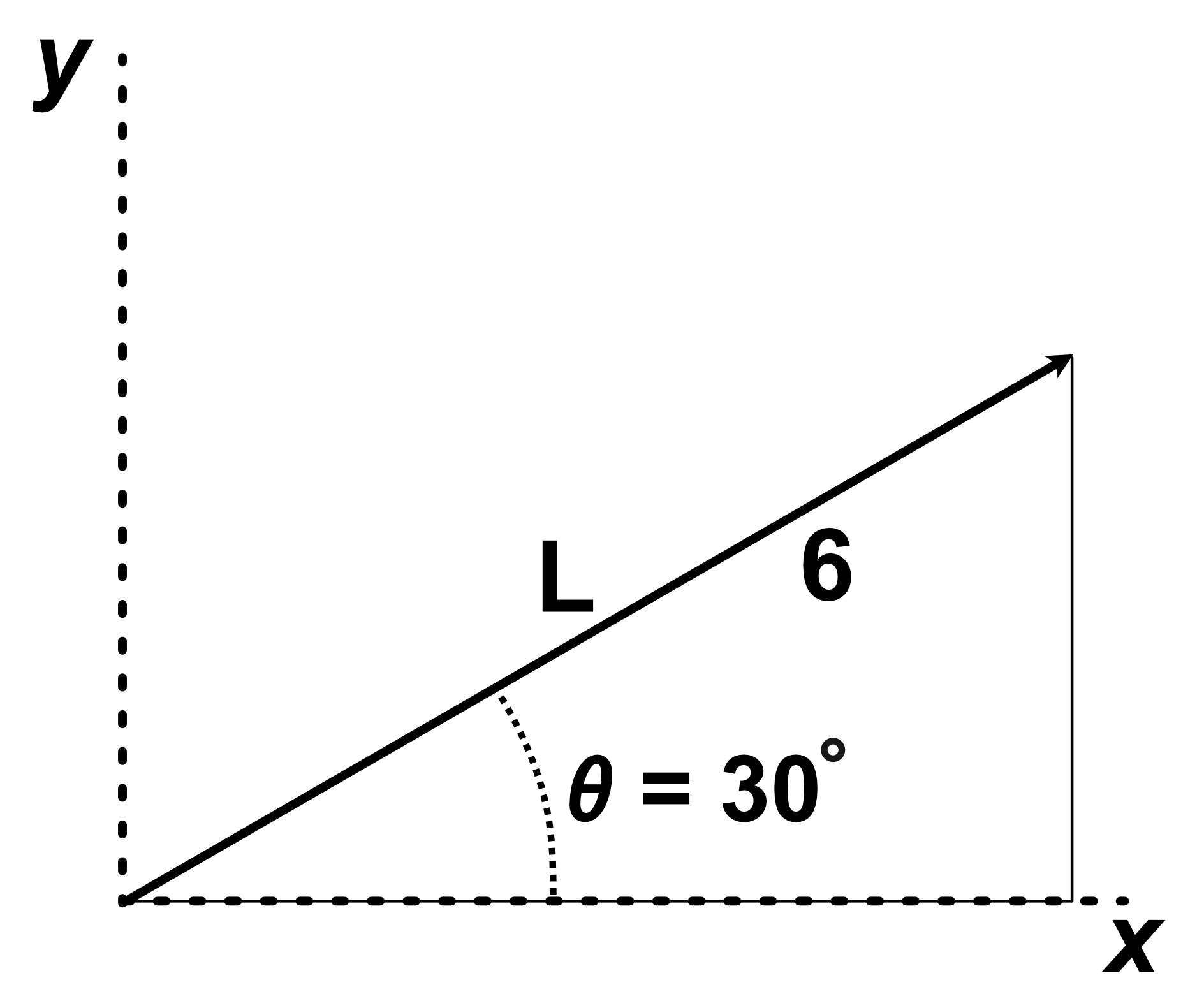
There are many occasions where it might be useful to determine the length of this line projected along the $x$ and $y$ directions. These projects form a right triangle. Remember our trigonometric functions:
$sin(\theta) = \frac{opposite}{hypotenuse}$
$cos(\theta) = \frac{adjacent}{hypotenuse}$
We can rearrange to obtain:
$opposite = hypotenuse*sin(\theta)$
$adjacent = hypotenuse*cos(\theta)$
Therefore, we obtain for the projected lengths:
$L_x = 6sin(30) = 3$
$L_y = 6cos(30) = 5.196$
Drawing Circular Motion
Suppose that we set $x = sin(t)$ and $y = cos(t)$ where $t$ represents time. If we then create a plot $(x,y)$, we observe that a circle is drawn.
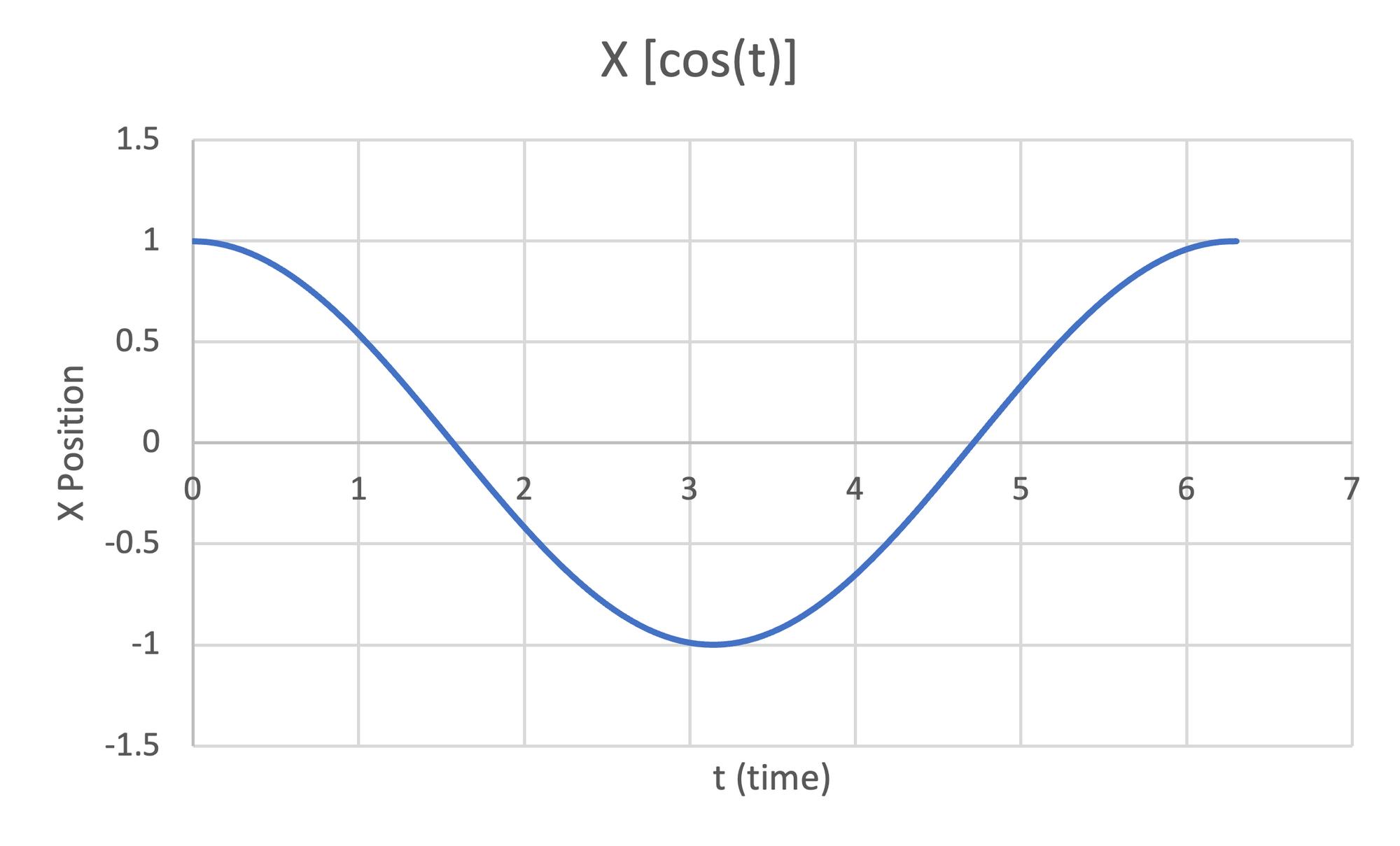
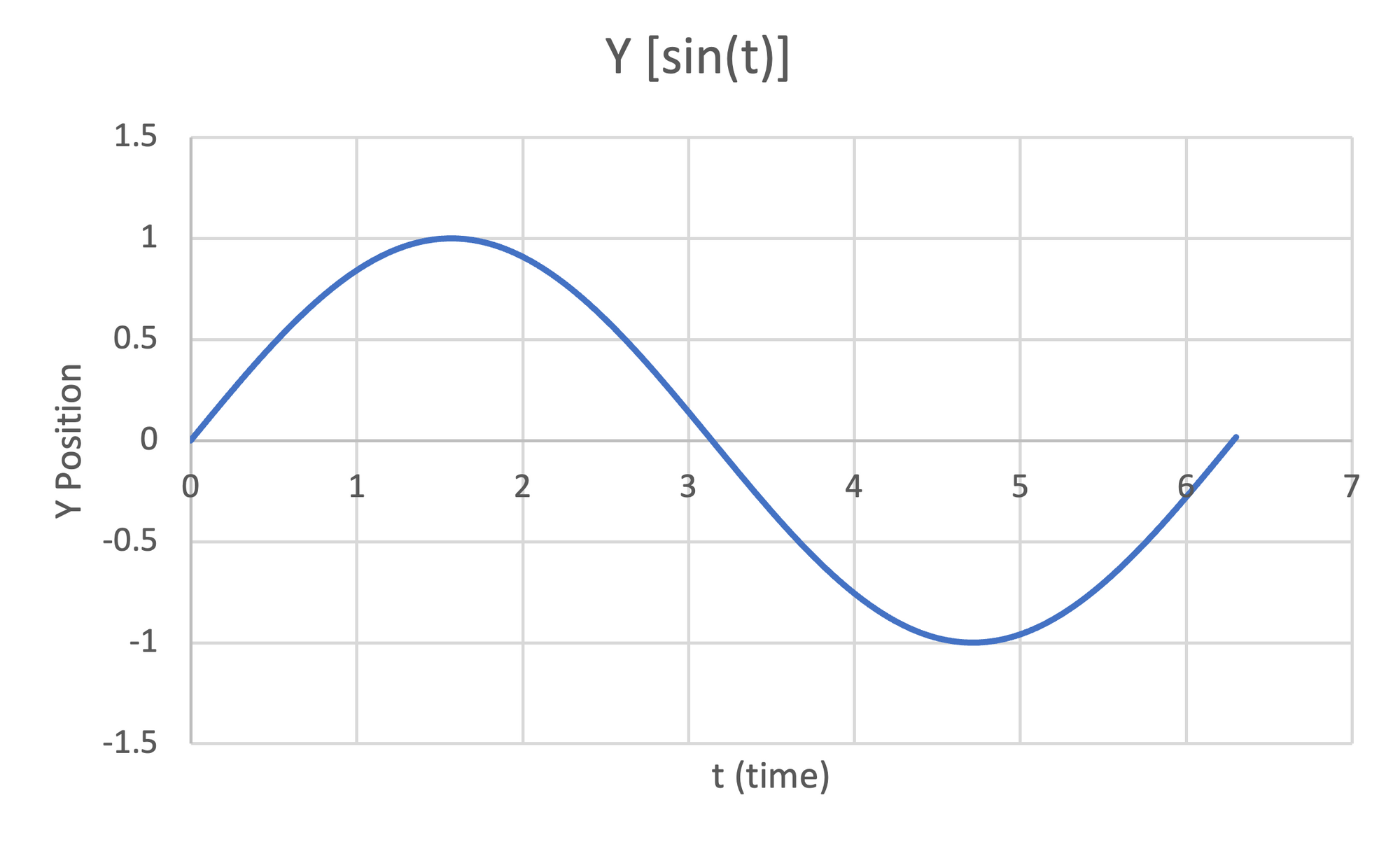
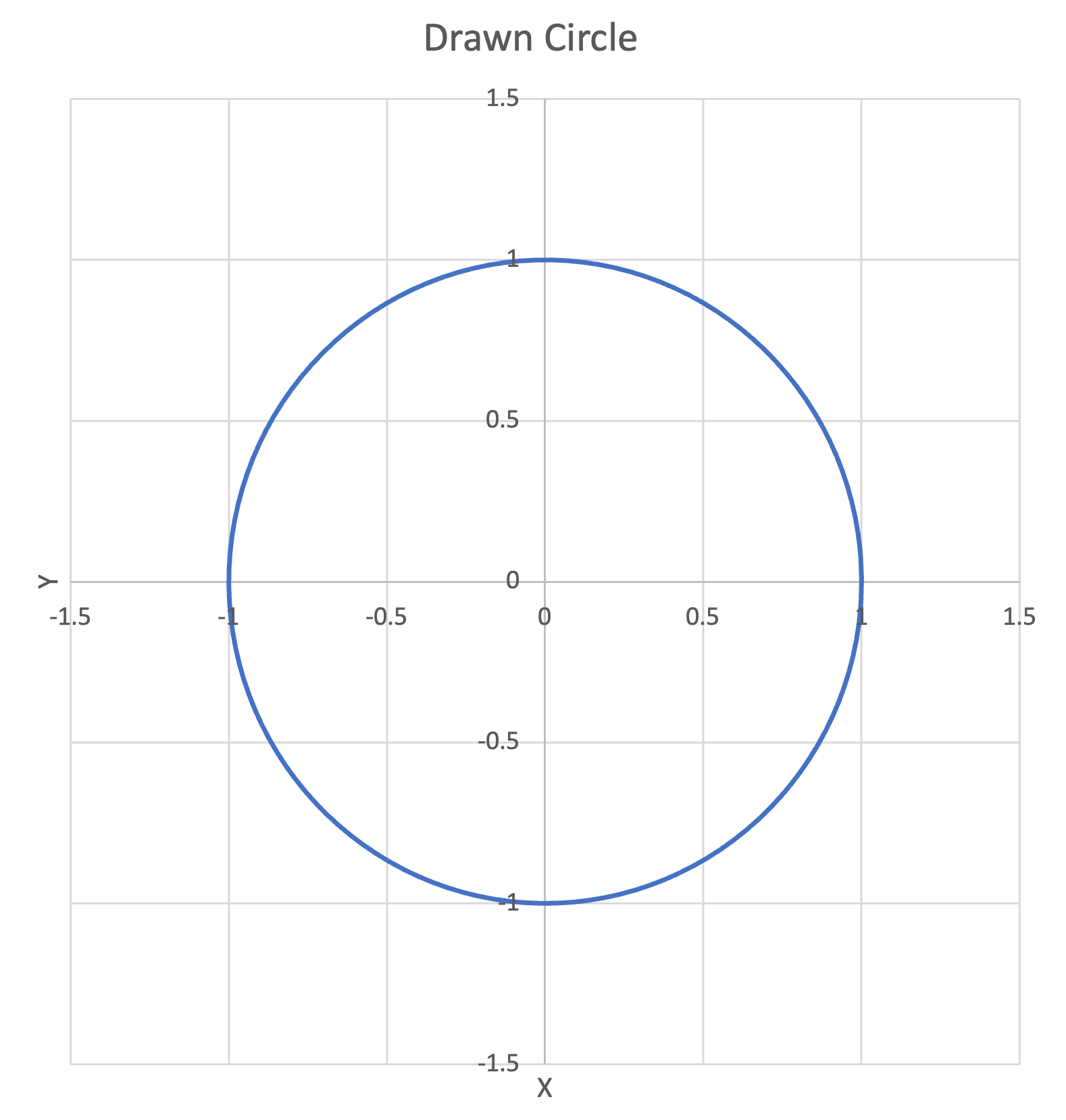
Figure 34:Left- Plot of $cos(t)$ for $0 \le t \le 2\pi$ | Center- Plot of $sin(t)$ for $0 \le t \le 2\pi$ | Right- Plot of $(cos(t),sin(t))$ for $0 \le t \le 2\pi$

