Vector Multiplication
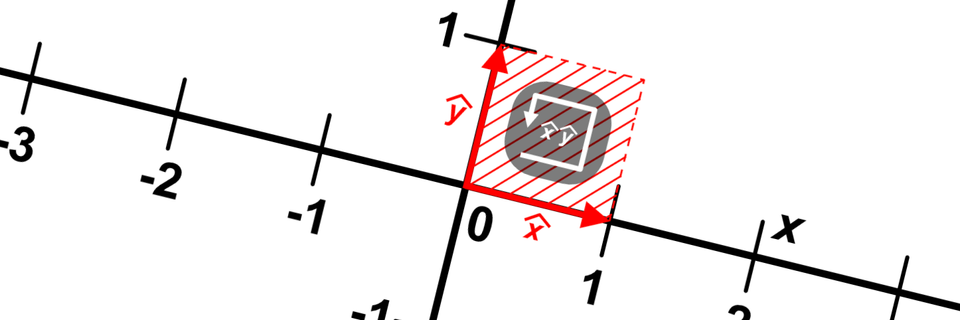
Required Prerequisites- Standard Vectors
The material in this article has far ranging application but on its own may appear abstract. As you read through this article you should work to understand the concepts presented but temporarily suspend desires to apply them. This material serves as a foundation and a gateway that will add value each time you read it. We will explore the usefulness of each concept in deeper detail later.
Squaring a Vector
Consider that we have the number $2$. We can also represent this number as a point on a number line. This is shown below graphically:

Suppose we multiply $2$ by itself to square it:
$$(2)(2) = 2^2 = 4$$
Once again, we can represent this squared number with a number line.
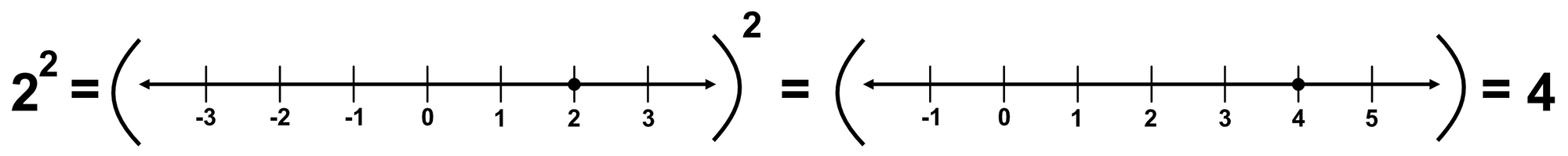
Let's return to back to our $2$ number line.

We can modify the number line by labeling it with "$x$". It's still just a number line.
Next, we can modify the number line by changing the marker from a dot to an arrow.

Finally, we can add a second number line perpendicular to the first and label it "$y$".
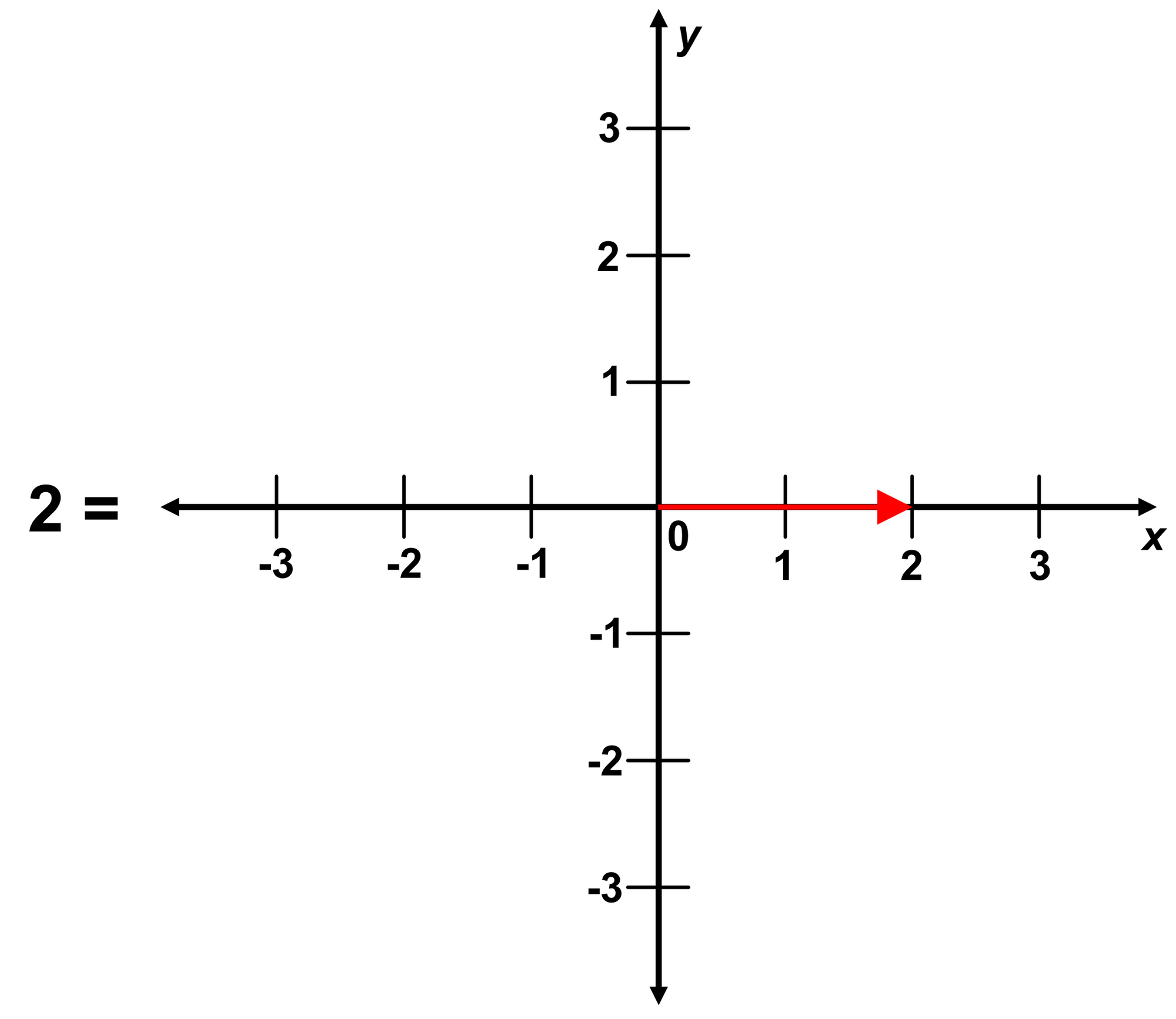
I'd like to emphasize, nothing has fundamentally changed. We've simply decorated our original number line.
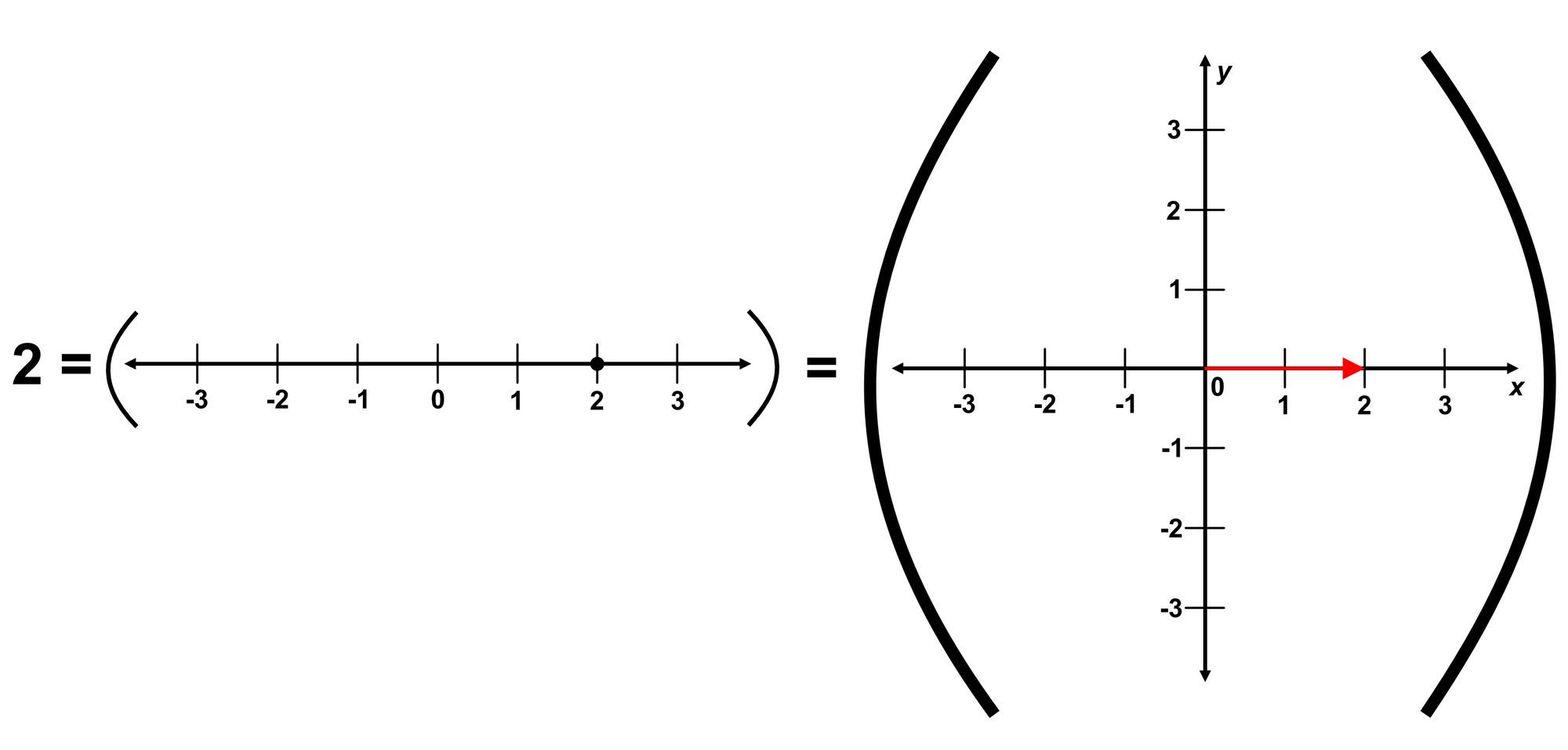
We can now notice that our decorated number line looks something like a vector. Let's call it $\overline{L}$.
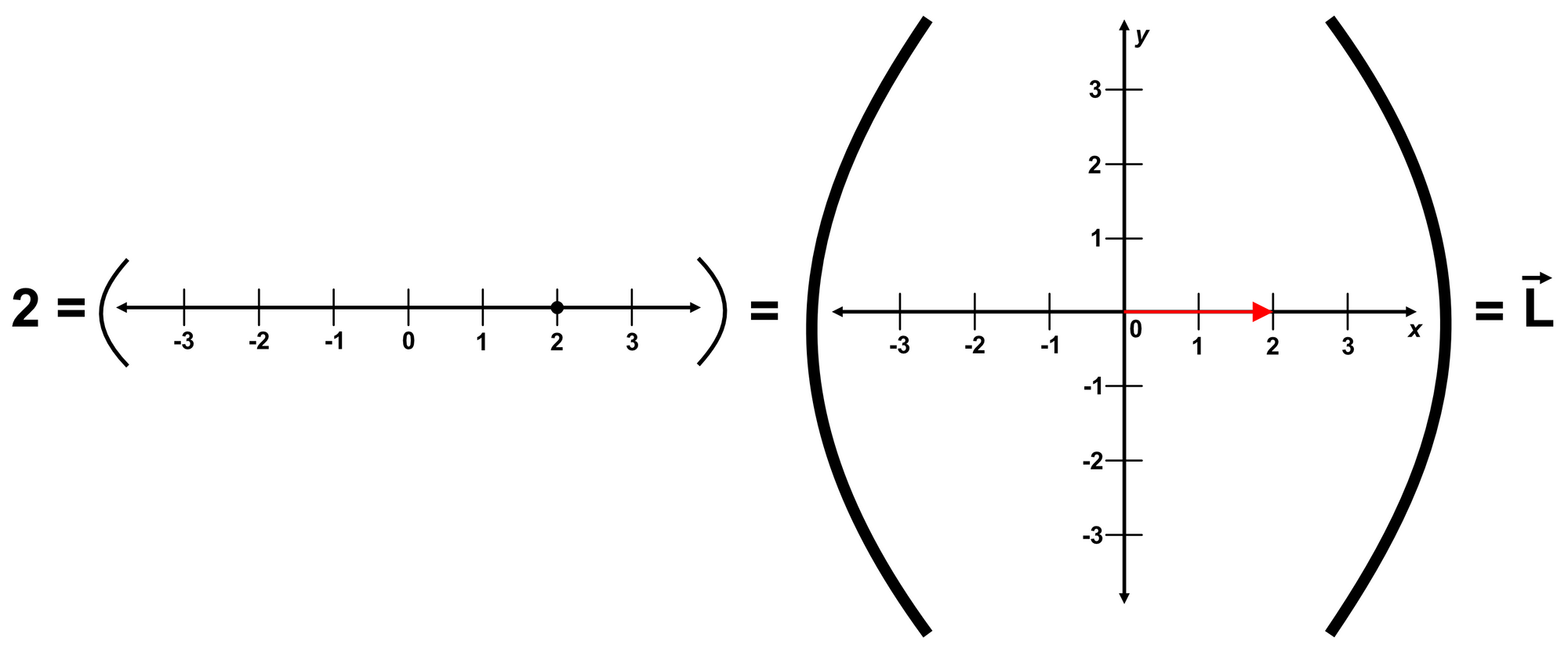
In this example, $\overline{L} = 2\hat{x} + 0\hat{y}$.
Let's once again multiply this number by itself to square it:
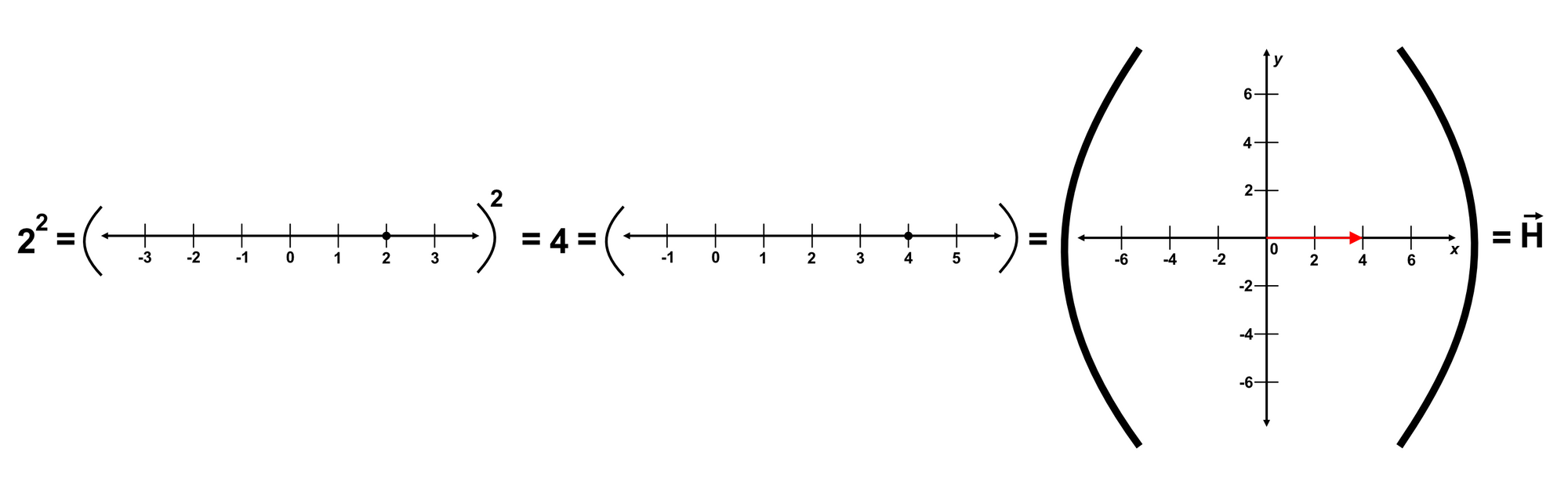
In this example, $\overline{H} = 4\hat{x} + 0\hat{y}$.
Through our decoration process, we obtained that $2 = 2\hat{x} + 0\hat{y} = \overline{L}$. We also obtained that $4 = 4\hat{x} + 0\hat{y} = \overline{H}$.
Since $2^2 = 4$, we are forced to conclude that:
$$2^2 = (2\hat{x} + 0\hat{y})^2 = \overline{L}^2 = 4 = (4\hat{x} + 0\hat{y}) = \overline{H}$$
We will focus on just one small part of this equality:
$$2^2 = (2\hat{x} + 0\hat{y})^2 = \boxed{\overline{L}^2 = 4} = (4\hat{x} + 0\hat{y}) = \overline{H}$$
$$\overline{L}^2 = 4$$
Squaring $\overline{L}$ results in a scalar!
Through the exact same decoration process, we can rotate our number line to the vertical orientation and progress to a similar state.
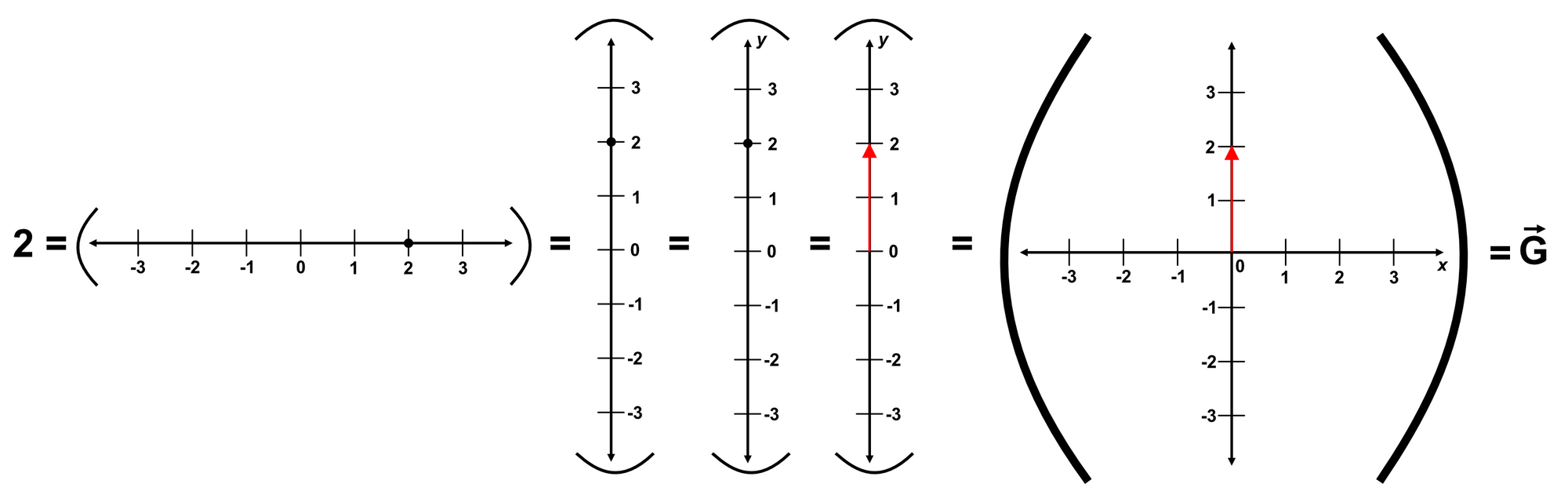
Once again, we end up with something resembling a vector which we can call $\overline{G}$.
$$\overline{G} = 0\hat{x} + 2\hat{y}$$
Let's again square our number:
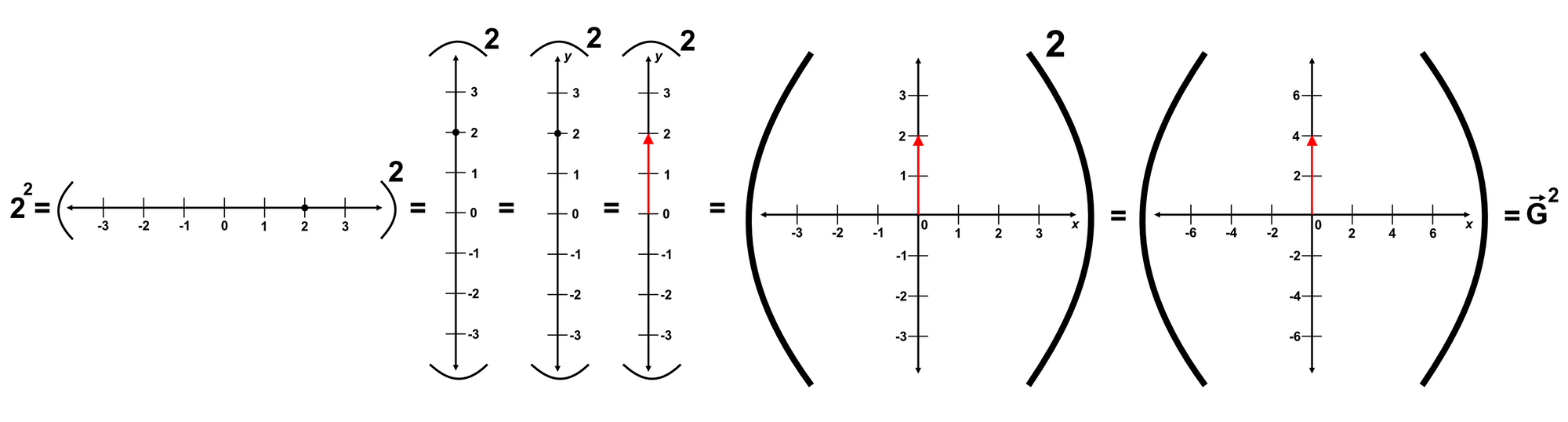
We obtain $\overline{G}^2 = 4$.
Since we've rotated our number line vertical, we might as well also rotate it to an arbitrary angle ($30^\circ$):
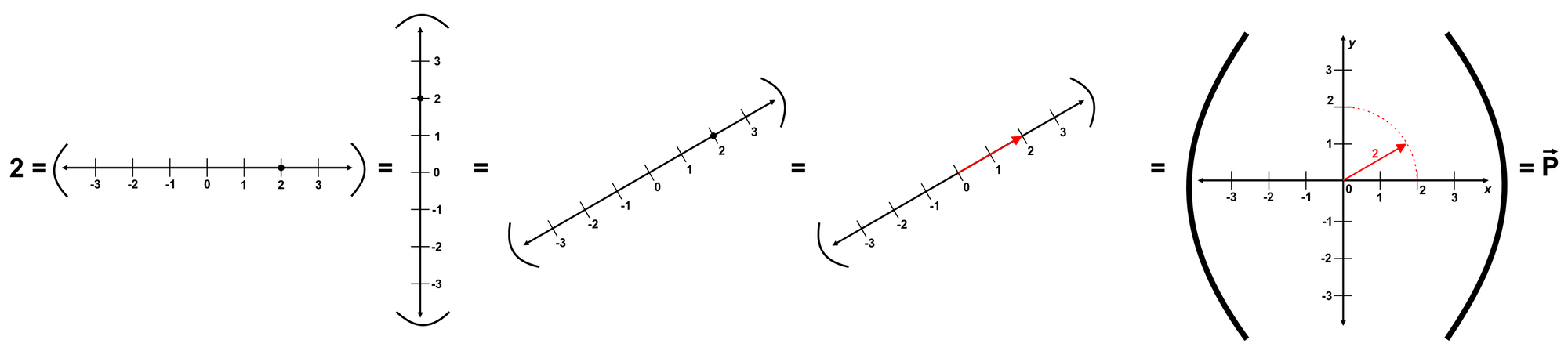
$2 = \overline{P} = 1.732\hat{x} + 1\hat{y}$
Once again, we square it:

We obtain $2^2 = \overline{P}^2 = (1.732\hat{x} + 1\hat{y})^2 = 4$.
We observe that all of these vectors $\overline{L}$, $\overline{G}$, and $\overline{P}$ have the same magnitude, $2$:
$||\overline{L}|| = ||\overline{G}|| = ||\overline{P}|| = 2$
We observe that the square of all of these vectors was equal to $4$, $\overline{L}^2 = \overline{G}^2 = \overline{P}^2 = 4$.
We observe that $4$ is the square of their magnitude, $||\overline{L}||^2 = 4$.
We therefore come to the conclusion that the square of all these vectors is equal to the square of their magnitude:
$$\overline{L}^2 = ||\overline{L}||^2$$
$$\overline{G}^2 = ||\overline{G}||^2$$
$$\overline{P}^2 = ||\overline{P}||^2$$
If we were to apply this analysis for any size vector at any angle, we would obtain the same result. The square of a vector $\overline{v}$ is equal to the square of its magnitude.
$$\boxed{\overline{v}^2 = ||\overline{v}||^2}$$
In many texts, this property is given as a fundamental statement without proof, but I felt it was important to intuitively motivate its existence.
Multiplying Two Dimensional Vectors
Suppose we have two generic 2D vectors:
$\overline{L}_1 = a_x\hat{x} + a_y\hat{y}$
$\overline{L}_2 = b_x\hat{x} + b_y\hat{y}$
Now we multiply them together:
$(\overline{L}_1)(\overline{L}_2)= (a_x\hat{x} + a_y\hat{y})(b_x\hat{x} + b_y\hat{y}) = (a_x b_x)\hat{x}^2 + (a_x b_y)\hat{x}\hat{y} + (a_y b_x)\hat{y}\hat{x} + (a_y b_y)\hat{y}^2 $
This seems fairly reasonable... except for the part where we have no idea what $\hat{x}^2$, $\hat{x}\hat{y}$, $\hat{y}\hat{x}$ and $\hat{y}^2$ are.
Exploring $\hat{x}^2$ & $\hat{y}^2$
$\hat{x}$ is the same as $(1)\hat{x}$ which is a vector of magnitude $1$ pointing along the $x$ axis:
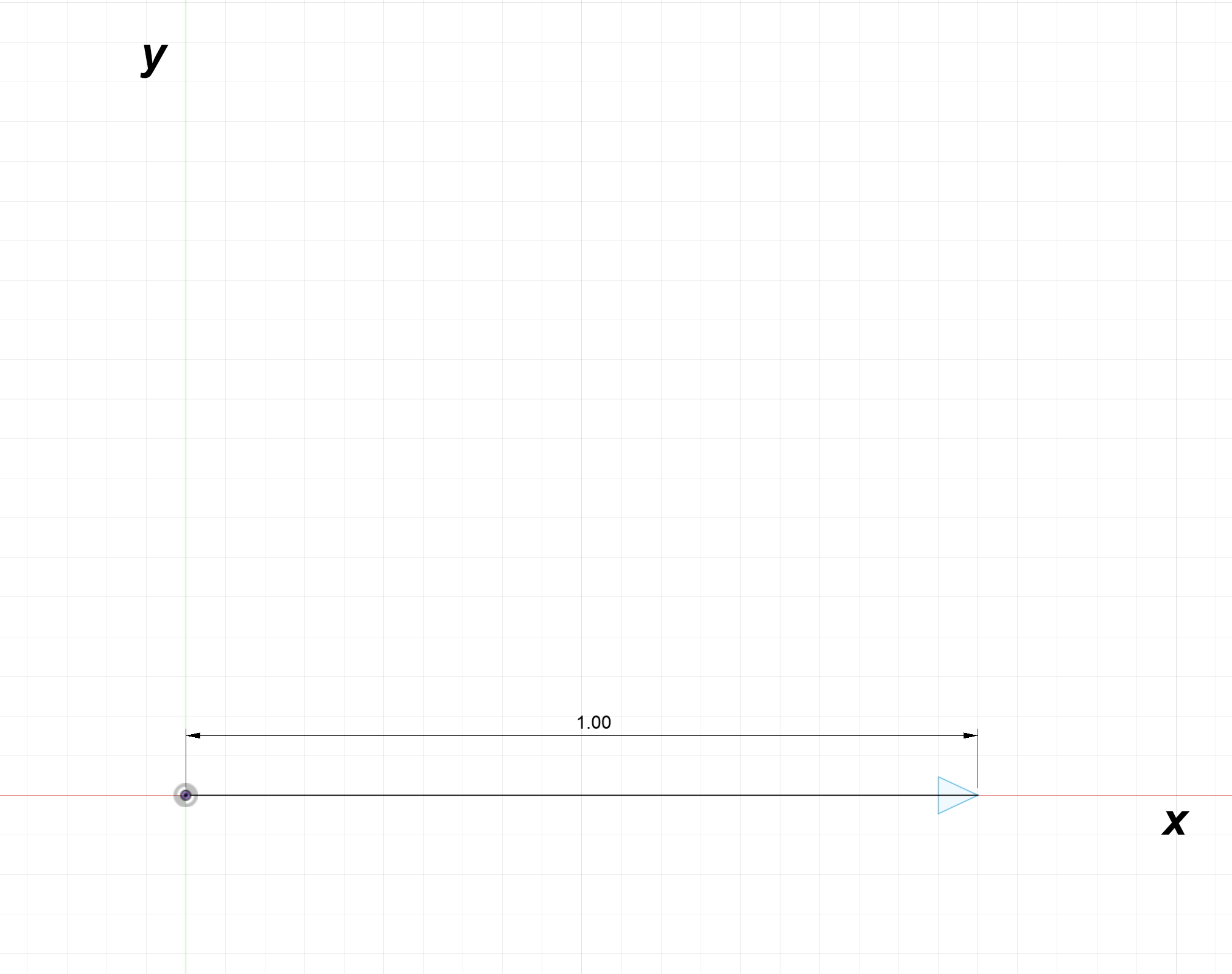
Recall our earlier identity, $\overline{v}^2 = ||\overline{v}||^2$.
Substituting in:
$$\hat{x}^2 = ||\hat{x}||^2$$
As already stated, $||\hat{x}|| = 1$. Therefore:
$$\boxed{\hat{x}^2 = ||\hat{x}||^2 = 1^2 = 1}$$
Through an identical analysis method, we obtain:
$$\boxed{\hat{y}^2 = ||\hat{y}||^2 = 1^2 = 1}$$
Substituting, we find:
$$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y)\hat{x}\hat{y} + (a_y b_x)\hat{y}\hat{x}$$
Exploring $\hat{x}\hat{y}$
Suppose we have a vector $\overline{L} = (1)\hat{x} + (1)\hat{y}$. Note that per the pythagorean theorem, $||\overline{L}||^2 = (1^2 + 1^2) = 2$. Using our identity $\overline{v}^2 = ||\overline{v}||^2$, we obtain:
$$\overline{L}^2 = ||\overline{L}||^2$$
$$(\hat{x} + \hat{y})^2 = || \hat{x} + \hat{y} ||^2 = 2$$
$$(\hat{x} + \hat{y})^2 = 2 $$
$$\hat{x}^2 + \hat{x}\hat{y} + \hat{y}\hat{x} + \hat{y}^2 = 2 $$
Remember from earlier that $\hat{x}^2 = \hat{y}^2 = 1$:
$$1 + \hat{x}\hat{y} + \hat{y}\hat{x} + 1 = 2 $$
$$\hat{x}\hat{y} + \hat{y}\hat{x} = 0 $$
$$\boxed{\hat{x}\hat{y} = -\hat{y}\hat{x}}$$
We are used to multiplication being commutative. $(2)(4) = (4)(2) = 8$. Here, we see that multiplication of vectors is NOT commutative, $\hat{x}\hat{y} \ne \hat{y}\hat{x}$.
With this information, we can simplify our original vector multiplication:
$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y)\hat{x}\hat{y} + (a_y b_x)\hat{y}\hat{x}$
$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y)\hat{x}\hat{y} + (a_y b_x)\left(-\hat{x}\hat{y}\right)$
$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y)\hat{x}\hat{y} - (a_y b_x)\hat{x}\hat{y}$
$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y - a_y b_x )\hat{x}\hat{y} $
We can also make one more crucial observation. Let's take the square of $\hat{x}\hat{y}$:
$$(\hat{x}\hat{y})^2 = (\hat{x}\hat{y})(\hat{x}\hat{y}) = \hat{x}\hat{y}\hat{x}\hat{y}$$
Recall from a moment ago that $\hat{x} \hat{y} = -\hat{y} \hat{x}$, so we can flip it to $\hat{y}\hat{x} = -\hat{x}\hat{y}$ and substitute for the middle two terms:
$$(\hat{x}\hat{y})^2 = \hat{x}\hat{y}\hat{x}\hat{y} = \hat{x}(\hat{y}\hat{x})\hat{y} = \hat{x}(-\hat{x}\hat{y})\hat{y}$$
$$(\hat{x}\hat{y})^2 = -(\hat{x}\hat{x})(\hat{y}\hat{y})$$
$$(\hat{x}\hat{y})^2 = -(\hat{x}^2\hat{y}^2)$$
From earlier, we know that $\hat{x}^2 = \hat{y}^2 = 1$. Substituting:
$$(\hat{x}\hat{y})^2 = -((1)(1)) = -1$$
$$(\hat{x}\hat{y})^2 = -1$$
Now, taking the square root:
$$\hat{x}\hat{y} = \sqrt{-1} $$
Remember from our discussion on quadratic functions that $\sqrt{-1}$ is the complex number $i$.
Therefore:
$$\boxed{\hat{x}\hat{y} = \sqrt{-1} = i}$$
$\hat{x}\hat{y} = i$!?!!? Snap. Given this, it would have been equivalent to write the multiplication of our two vectors $\overline{L}_1$ and $\overline{L}_2$ as:
$$(\overline{L}_1)(\overline{L}_2) = (a_x b_x + a_y b_y) + (a_x b_y - a_y b_x )i$$
We will be doing this. We will be doing this all the time. Complex numbers are incredibly pervasive in advanced mathematics and physics. Their relevance comes from the unremarkable process of multiplying vectors!
Clearly $\hat{x}\hat{y}$ isn't a vector... we call it a bivector. Because $i = \hat{x}\hat{y}$, the complex number $i$ is also a bivector. We won't talk much more about complex numbers in this article, but it's crucial to recognize that this is where their applicability is born.
Visualizing $\hat{x} \hat{y}$ is somewhat challenging. Its generally best understood as an area with a rotational direction. The bivector $(1)\hat{x} \hat{y}$ has area $1$ and has a counter-clockwise rotation direction.
Remember that for multiplication, bivectors are negative commutative, $\hat{x} \hat{y} = -\hat{y} \hat{x}$. This corresponds to flip in the direction of rotation.

If these visualizations of bivectors are intimidating and unintuitive, don't be concerned. Unlike vectors, a visual intuition of bivectors is not needed.
2D Vector Multiplication
Given our prior work, we now recognize how to multiply two 2D vectors:
$$\boxed{\overline{L}_1 \overline{L}_2 = (a_x b_x + a_y b_y) + (a_x b_y - a_y b_x )\hat{x}\hat{y}}$$
If you are not yet familiar with vector mathematics, the above should be fairly straightforward. We've come about its derivation through a logical path.
If you are familiar with vector mathematics, the above should shatter the very core of what you believe vector multiplication means. In most mathematics education programs, students are taught that raw vector multiplication isn't possible, that we have to be specific about what kind of multiplication (typically the dot or cross product). Wrong. This isn't math I invented either; it's called Geometric Algebra. It was invented by William Kingdon Clifford in 1878.
The 2D vector product consists of two parts, a scalar part and a bivector part. We call the part corresponding to the scalar part of the product the dot product (symbolized by $\overline{L}_1 \cdot \overline{L}_2 $) and the part corresponding to the bivector part the wedge product (symbolized by $\overline{L}_1 \wedge \overline{L}_2 $):
$$\overline{L}_1 \overline{L}_2 = \underbrace{(a_x b_x + a_y b_y)}_{\overline{L}_1 \cdot \overline{L}_2 } + \underbrace{(a_x b_y - a_y b_x )\hat{x}\hat{y}}_{\overline{L}_1 \wedge \overline{L}_2}$$
We define the vector product as the sum of the dot and wedge products:
$$\boxed{\overline{L}_1 \overline{L}_2 = \overline{L}_1 \cdot \overline{L}_2 + \overline{L}_1 \wedge \overline{L}_2}$$
$$\boxed{\overline{L}_1 \cdot \overline{L}_2 = a_xb_x + a_yb_y}$$
$$\boxed{\overline{L}_1 \wedge \overline{L}_2 = (a_xb_y - a_yb_x)\hat{x}\hat{y}}$$
Multiplying Three Dimensional Vectors
Suppose we have two 3D vectors:
$\overline{L}_1 = a_x\hat{x} + a_y\hat{y} + a_z\hat{z}$
$\overline{L}_2 = b_x\hat{x} + b_y\hat{y} + b_z\hat{z}$
Now we multiply them together:
$$(\overline{L}_1)(\overline{L}_2) = ( a_x\hat{x} + a_y\hat{y} + a_z\hat{z})(b_x\hat{x} + b_y\hat{y} + b_z\hat{z}) $$
Distributing and multiplying, we obtain:
$$(\overline{L}_1)(\overline{L}_2) = (a_x b_x)\hat{x}^2 + (a_y b_y)\hat{y}^2 + (a_z b_z)\hat{z}^2$$
$$ + (a_x b_y)\hat{x}\hat{y} + (a_y b_x)\hat{y}\hat{x} $$
$$ + (a_x b_z)\hat{x}\hat{z} + (a_z b_x)\hat{z}\hat{x} $$
$$ + (a_y b_z)\hat{y}\hat{z} + (a_z b_y)\hat{z}\hat{y} $$
Remember from the 2D discussion that a squared unit vector equals $1$, $\hat{x}^2 = \hat{y}^2 = \hat{z}^2 = 1$. Also recall that a bivector is equal to it's own negative, $\hat{y}\hat{x} = -\hat{x}\hat{y}$, $\hat{z}\hat{x} = -\hat{x}\hat{z}$, $\hat{z}\hat{y} = -\hat{y}\hat{z}$:
$$(\overline{L}_1)(\overline{L}_2) = (a_x b_x)(1) + (a_y b_y)(1)+ (a_z b_z)(1)$$
$$ + (a_x b_y)\hat{x}\hat{y} - (a_y b_x)\hat{x}\hat{y} $$
$$ + (a_x b_z)\hat{x}\hat{z} - (a_z b_x)\hat{x}\hat{z} $$
$$ + (a_y b_z)\hat{y}\hat{z} - (a_z b_y)\hat{y}\hat{z} $$
Simplifying:
$$(\overline{L}_1)(\overline{L}_2) = a_x b_x + a_y b_y + a_z b_z $$
$$ + (a_x b_y - a_y b_x)\hat{x}\hat{y}$$
$$ + (a_x b_z - a_z b_x)\hat{x}\hat{z} $$
$$ + (a_y b_z - a_z b_y)\hat{y}\hat{z} $$
Similar to the 2D vector multiplication, we have scalar and bivector components $\hat{x}\hat{y}$, $\hat{x}\hat{z}$, and $\hat{y}\hat{z}$ which we similarly associate with the dot and wedge product:
$$\boxed{\overline{L}_1 \cdot \overline{L}_2 = a_x b_x + a_y b_y + a_z b_z }$$
$$\boxed{ \overline{L}_1 \wedge \overline{L}_2 = (a_x b_y - a_y b_x)\hat{x}\hat{y} + (a_x b_z - a_z b_x)\hat{x}\hat{z} + (a_y b_z - a_z b_y)\hat{y}\hat{z} }$$
$$\boxed{(\overline{L}_1) (\overline{L}_2) = \overline{L}_1 \cdot \overline{L}_2 + \overline{L}_1 \wedge \overline{L}_2}$$
The Cross Product
Let's take another look at the definition for the 3D wedge product:
$$\overline{L}_1 \wedge \overline{L}_2 = (a_x b_y - a_y b_x)\hat{x}\hat{y} + (a_x b_z - a_z b_x)\hat{x}\hat{z} + (a_y b_z - a_z b_y)\hat{y}\hat{z}$$
In the late 1800's, in parallel with Clifford's development of Geometric Algebra, Josiah Willard Gibbs and Oliver Heaviside decided that one method of thinking about bivectors was by replacing them with a vector perpendicular to both vectors in the bivector. To figure out what to replace them with, they used the Right-hand Rule. For a bivector $\hat{x}\hat{y}$, point your index finger along the first vector and your middle finger along the second vector. Your thumb points in the direction to substitute for the bivector.
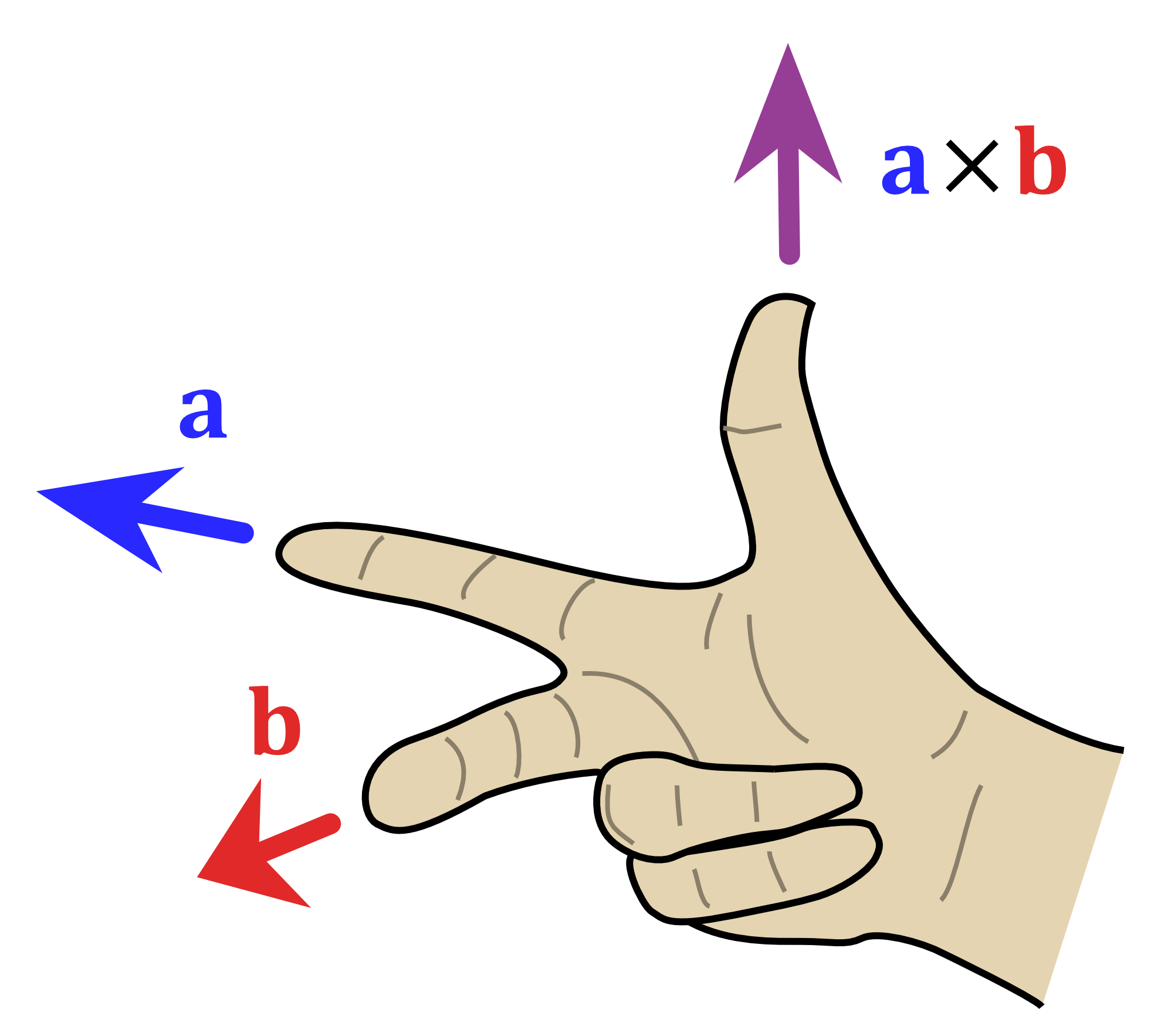
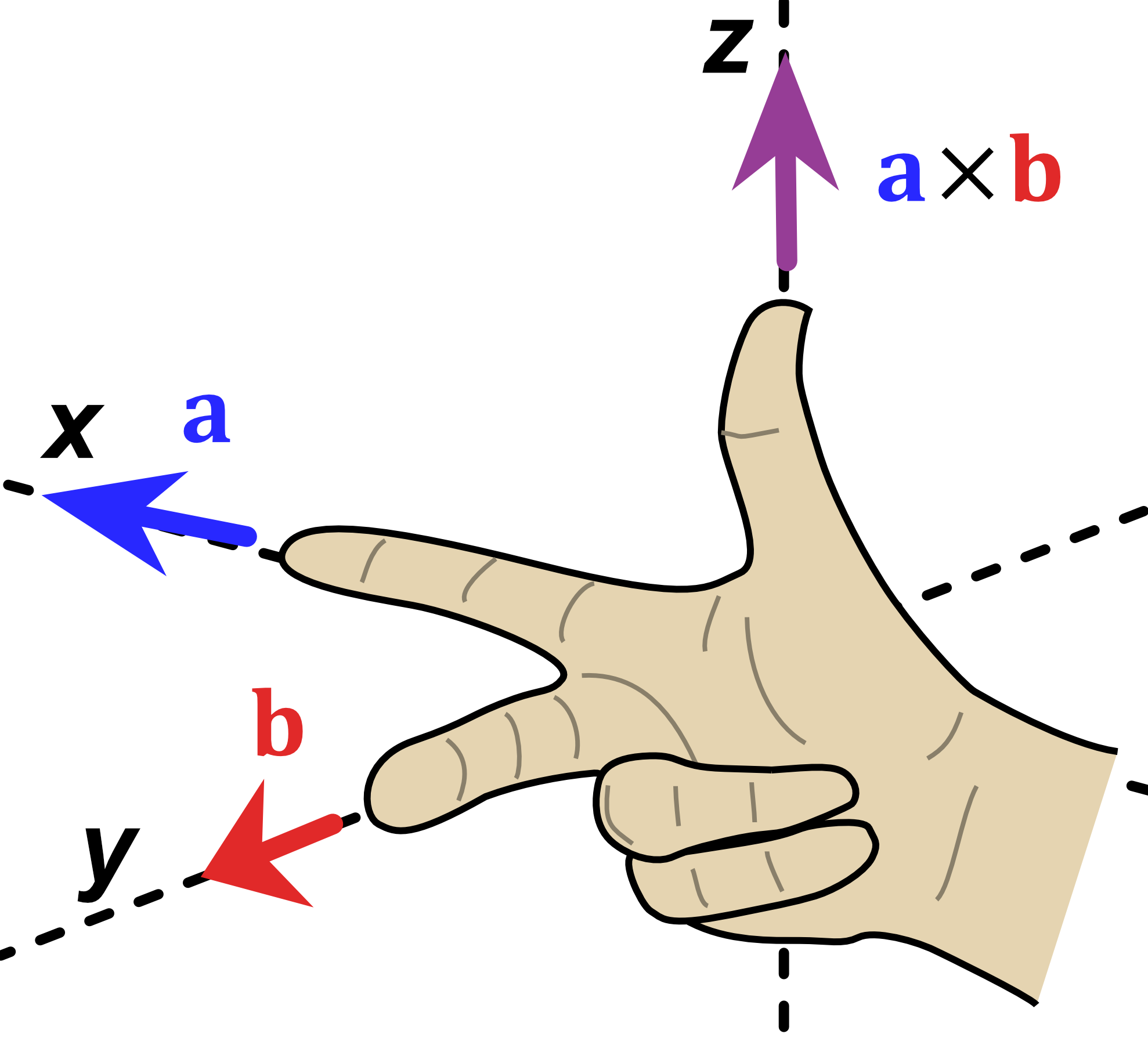
Figure 16:Left- Right-hand rule diagram | Right- Diagram of $\hat{x} \times \hat{y}$, modified from original | Original Image Citation- Acdx, Right hand rule cross product, CC BY-SA 3.0
Using this method, $\hat{x}\hat{y}$ would be replaced with $\hat{z}$.
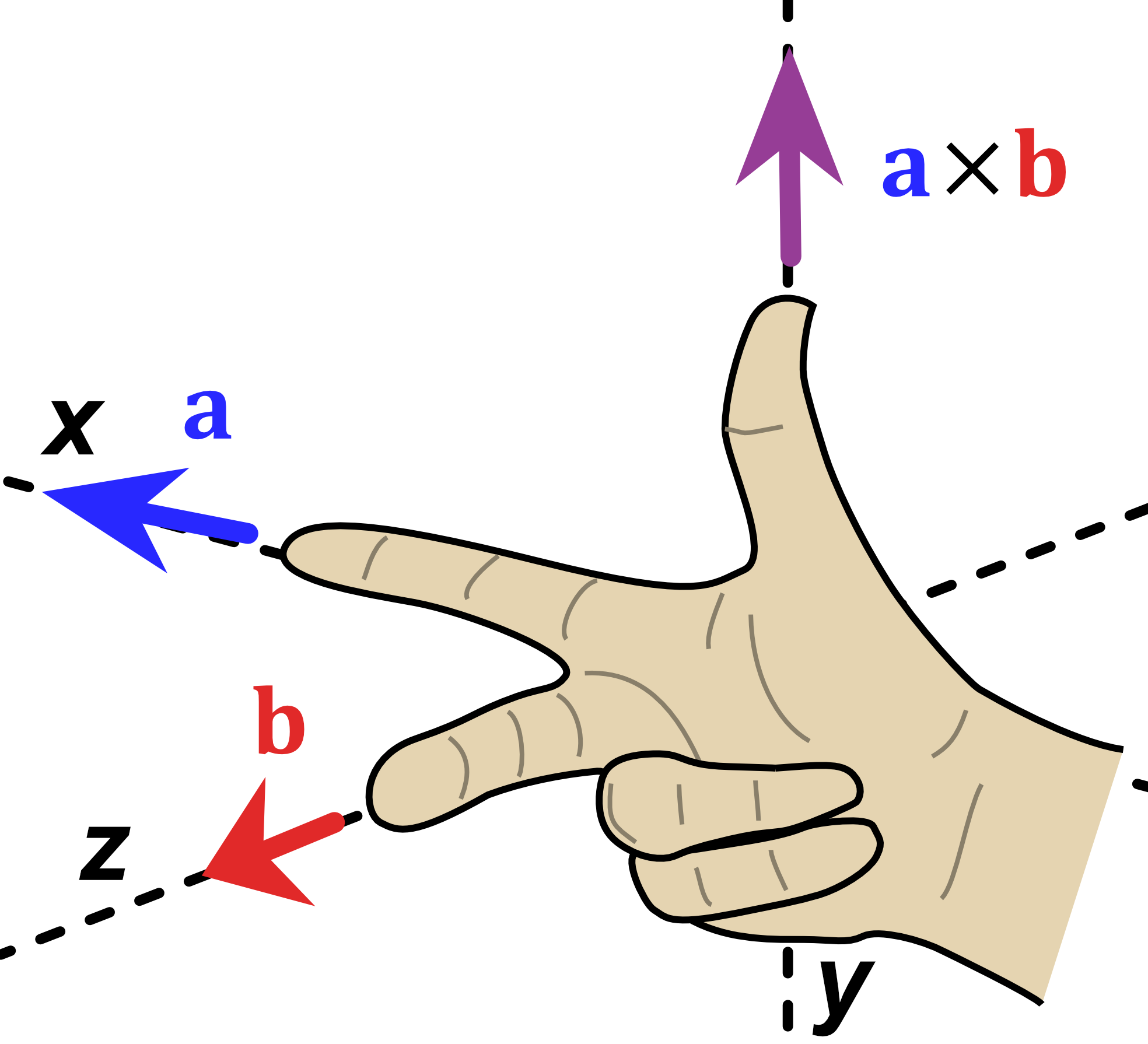
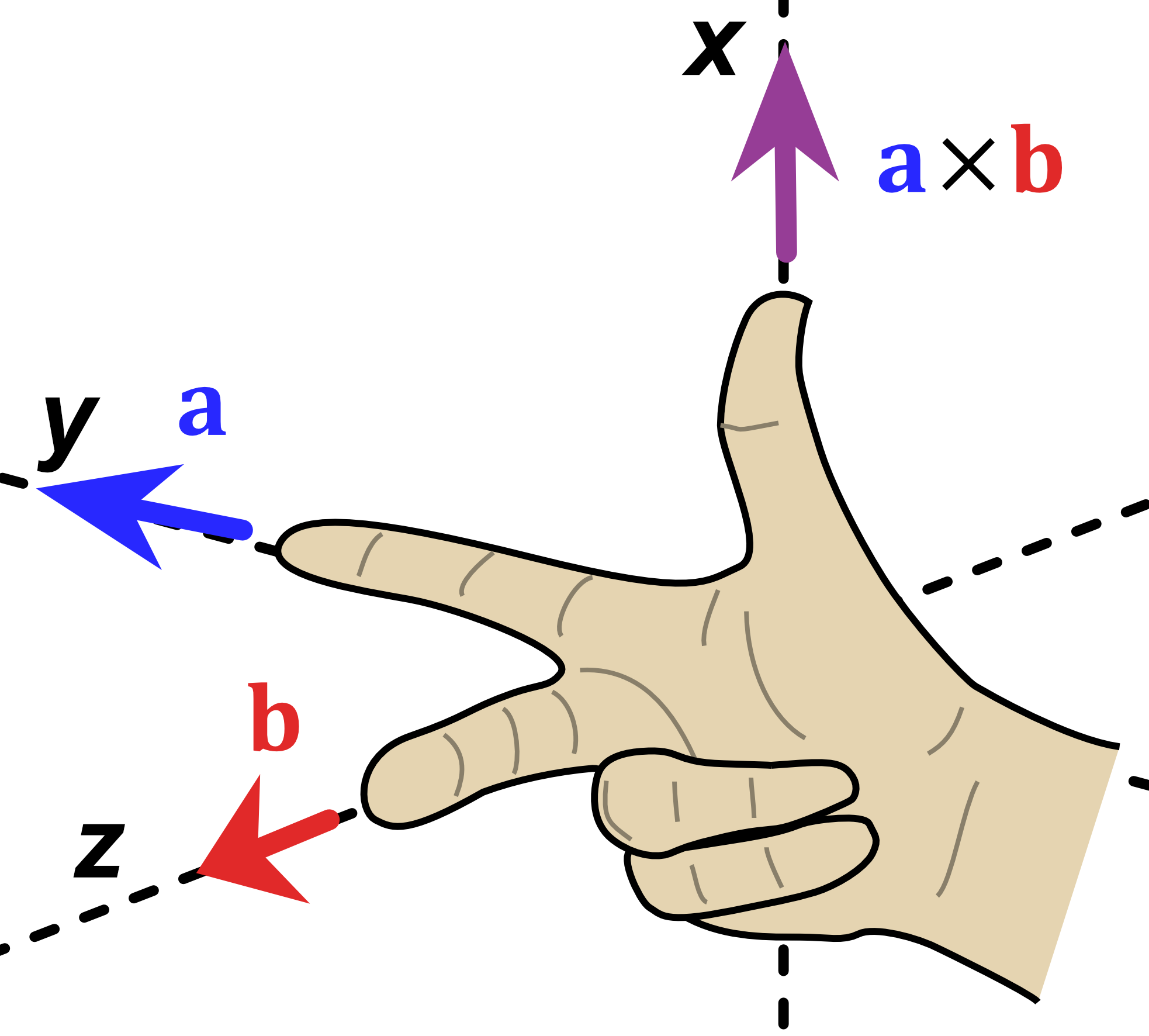
Figure 17:Left- Diagram of $\hat{x} \times \hat{z}$, modified from original | Right- Diagram of $\hat{y} \times \hat{z}$, modified from original | Original Image Citation- Acdx, Right hand rule cross product, CC BY-SA 3.0
Similarly, we find that:
$$\hat{x}\hat{z} \rightarrow -\hat{y}$$
$$\hat{y}\hat{z} \rightarrow \hat{x}$$
If we repeated the exercise for the flipped bivectors, we obtain:
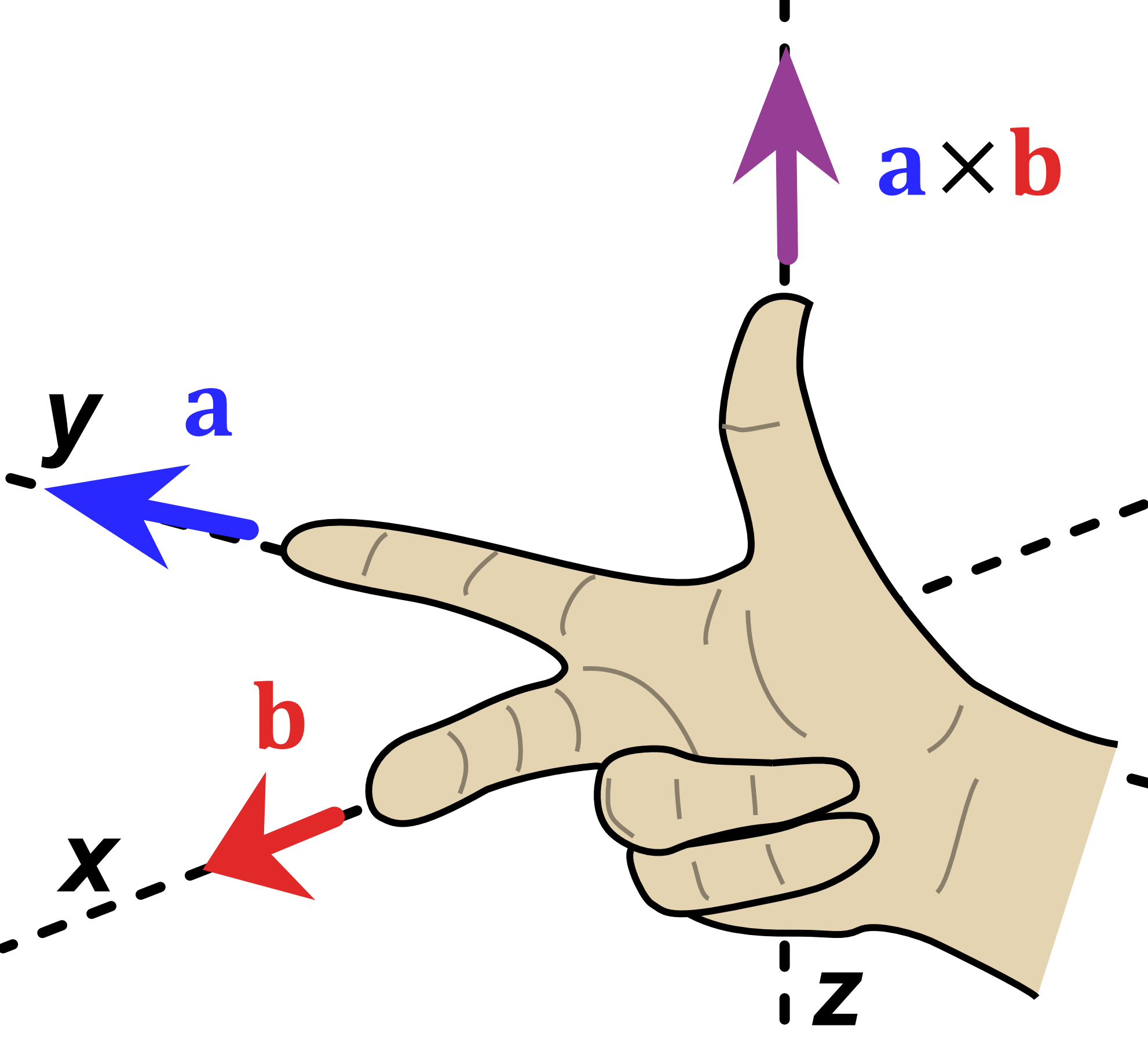
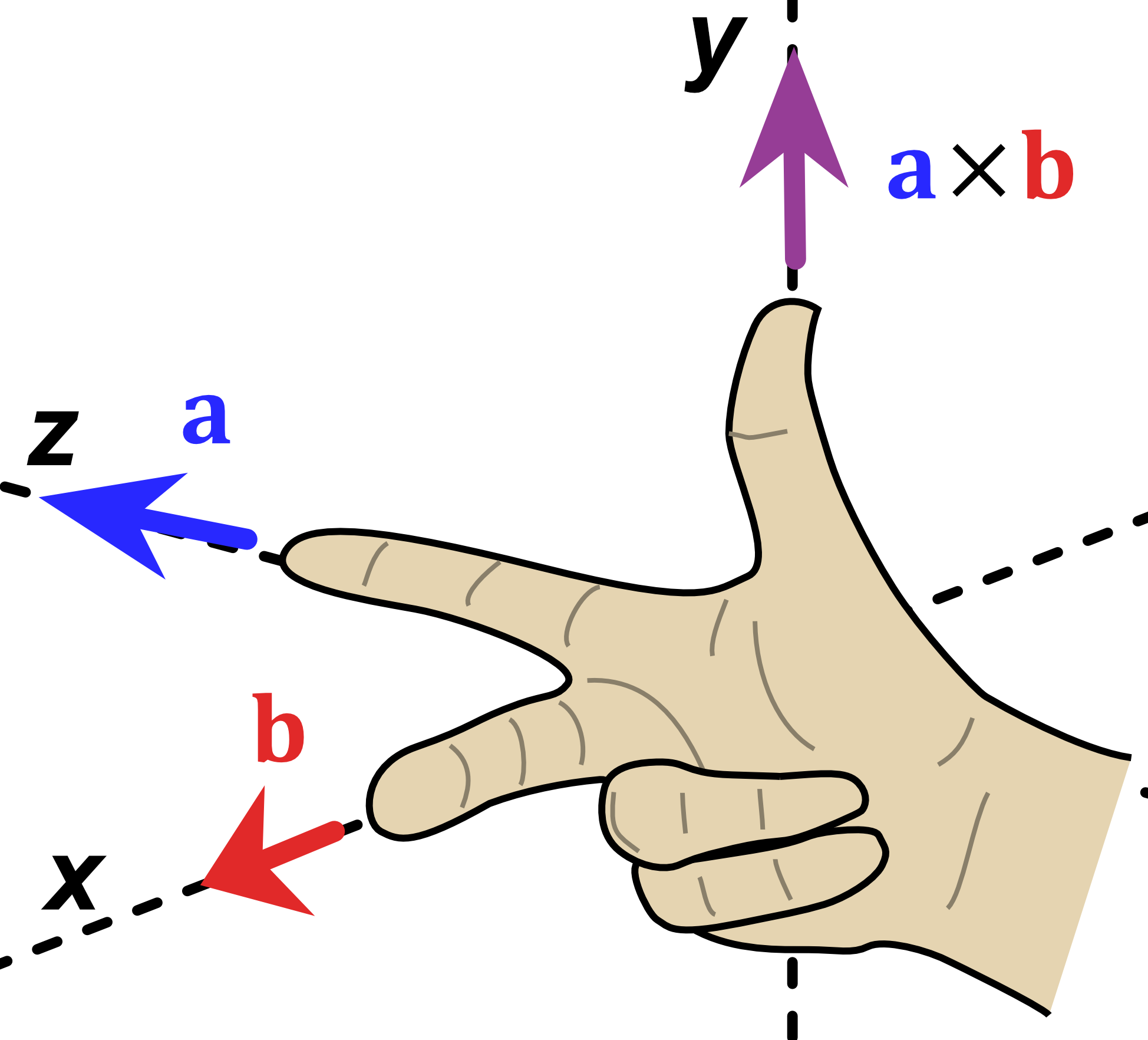
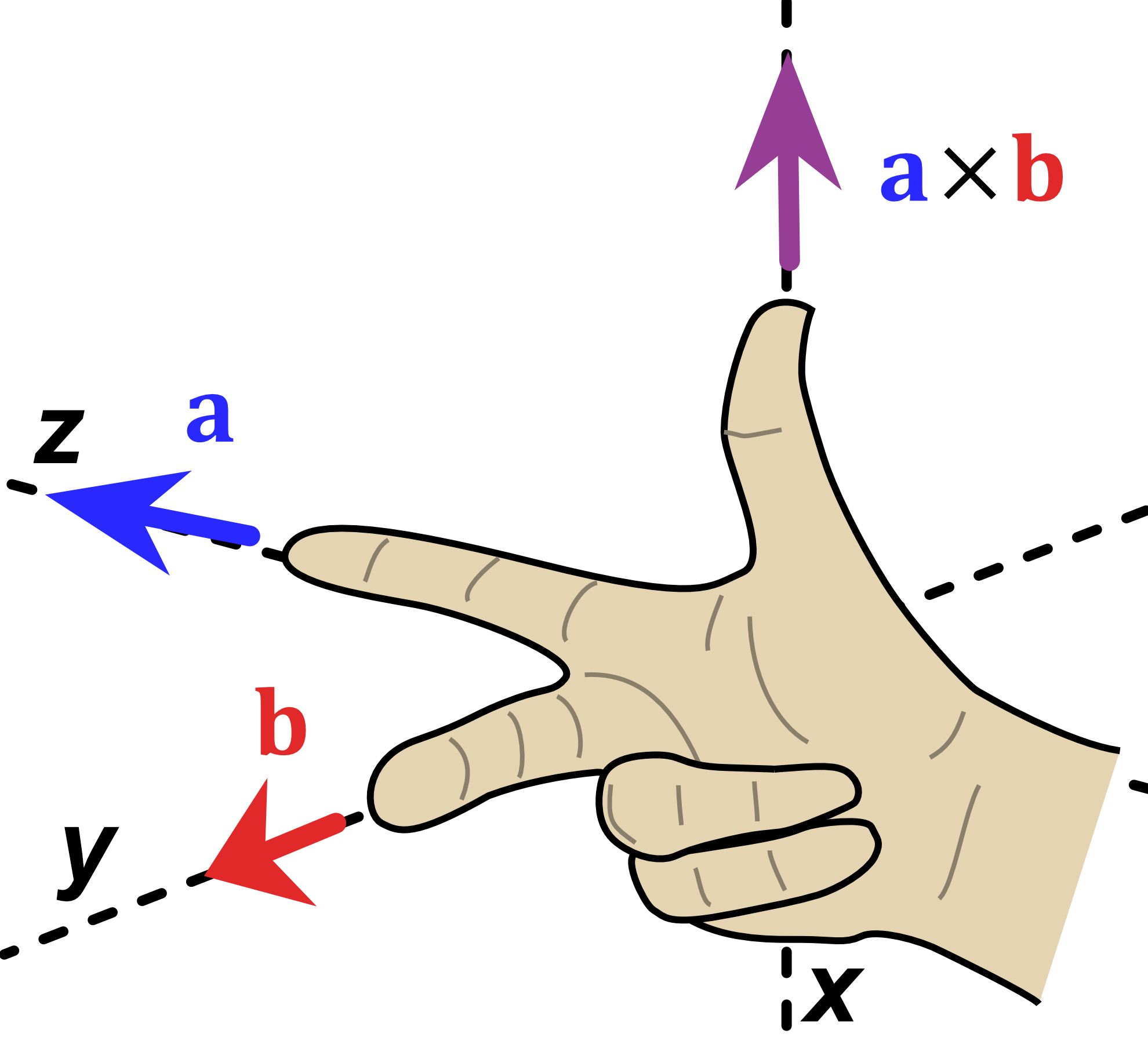
Figure 18:Left- Diagram of $\hat{y} \times \hat{x}$, modified from original | Center- Diagram of $\hat{z} \times \hat{x}$, modified from original | Right- Diagram of $\hat{z} \times \hat{y}$, modified from original | Original Image Citation- Acdx, Right hand rule cross product, CC BY-SA 3.0
$$\hat{y} \hat{x} \rightarrow -\hat{z}$$
$$\hat{z} \hat{x} \rightarrow \hat{y}$$
$$\hat{z} \hat{y} \rightarrow -\hat{x}$$
This should be especially reasonable when we remember that flipped bivectors are negatives of each other. Substituting these into our original wedge product, we obtain the cross product:
$$\overline{L}_1 \times \overline{L}_2 = (a_x b_y - a_y b_x)\hat{z} - (a_x b_z - a_z b_x)\hat{y}+ (a_y b_z - a_z b_y)\hat{x}$$
Simplifying:
$$\boxed{\overline{L}_1 \times \overline{L}_2 =(a_y b_z - a_z b_y)\hat{x} - (a_x b_z - a_z b_x)\hat{y}+ (a_x b_y - a_y b_x)\hat{z} }$$
The 2D Cross Product
The cross product was defined in context of 3D vectors, however if we pretent that a 2D vector is a 3D vector with $0$ $\hat{z}$ component, then we can take the cross product of two 2D vectors:
$\overline{L}_1 = a_x\hat{x} + a_y\hat{y} + 0\hat{z}$
$\overline{L}_2 = b_x\hat{x} + b_y\hat{y} + 0\hat{z}$
The resulting cross product is:
$$\overline{L}_1 \times \overline{L}_2 =(a_y b_z - a_z b_y)\hat{x} - (a_x b_z - a_z b_x)\hat{y}+ (a_x b_y - a_y b_x)\hat{z} $$
Substituting:
$$\overline{L}_1 \times \overline{L}_2 =(a_y (0) - (0) b_y)\hat{x} - (a_x (0) - (0) b_x)\hat{y}+ (a_x b_y - a_y b_x)\hat{z}$$
$$\boxed{\overline{L}_1 \times \overline{L}_2 = (a_x b_y - a_y b_x)\hat{z}}$$
Multivectors
In an earlier article describing Standard Vectors, we defined vectors as a mathematical object with direction and magnitude; we represented it by its components. For example a 3D vector was represented by:
$$\overline{L} = a_x\hat{x} + a_y\hat{y} + a_z \hat{z}$$
A multivector is any sum of vector-like components (including scalars). On this site, I will symbolize multivectors with a bold character, $\textbf{M}$. For example, the below multivector contains a scalar component, $\hat{x}$, $\hat{z}$, and $\hat{x} \hat{y}$ components:
$$\textbf{M} = a_s + a_x\hat{x} + a_z \hat{z} + b_{xy} \hat{x} \hat{y}$$

