Defining Pi.
Prerequisites Required- None
While this is a short a simple article, the topic is of immense importance.
$\pi$ is one of the most common mathematical symbols. Though it ends up in countless formula and applications, it has a very specific meaning.
Consider we have a circle of diameter $1$ ($mm$, $in$, etc.)
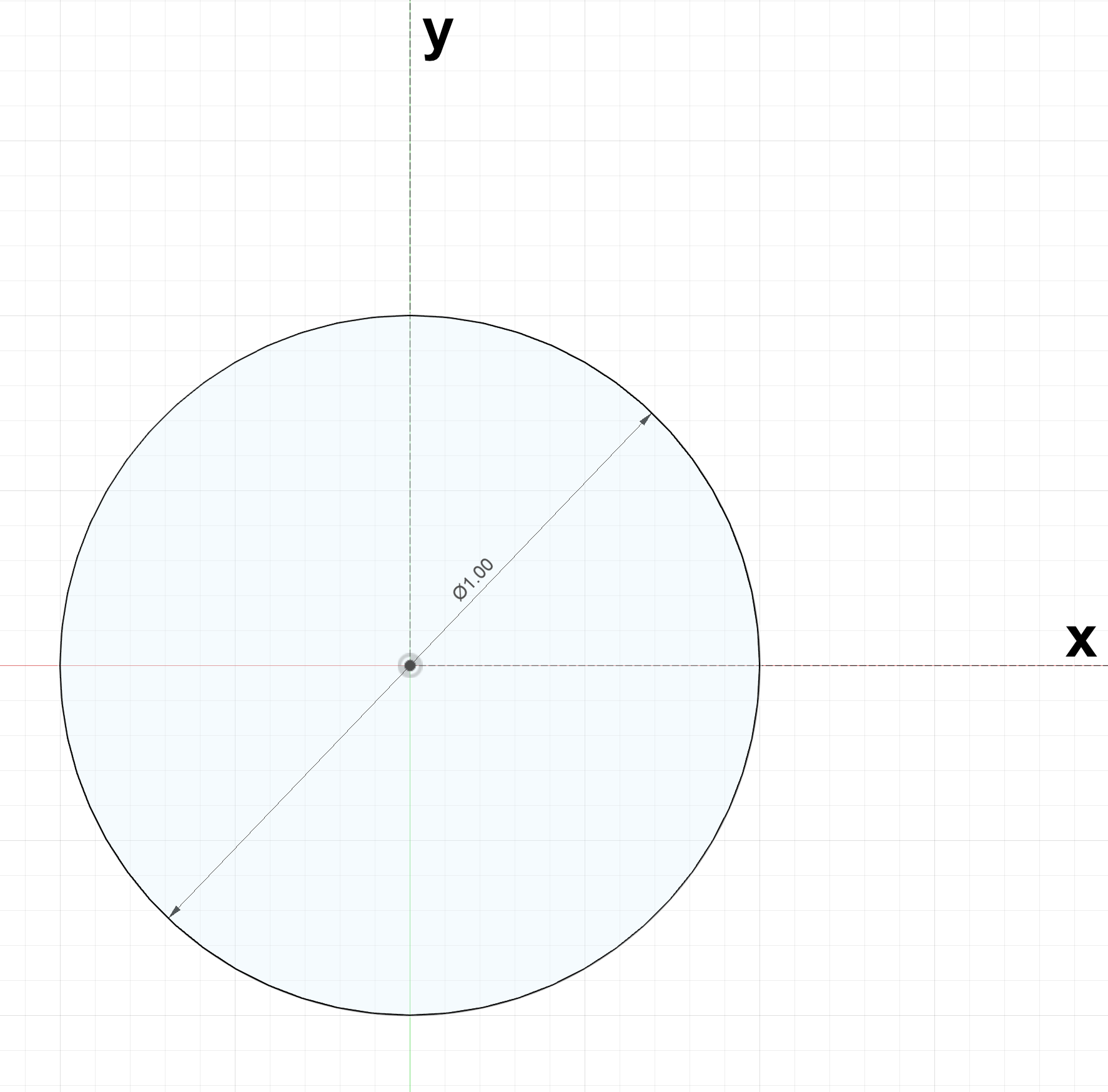
$\pi$ is the length to go around a circle of diameter $1$, its circumference.
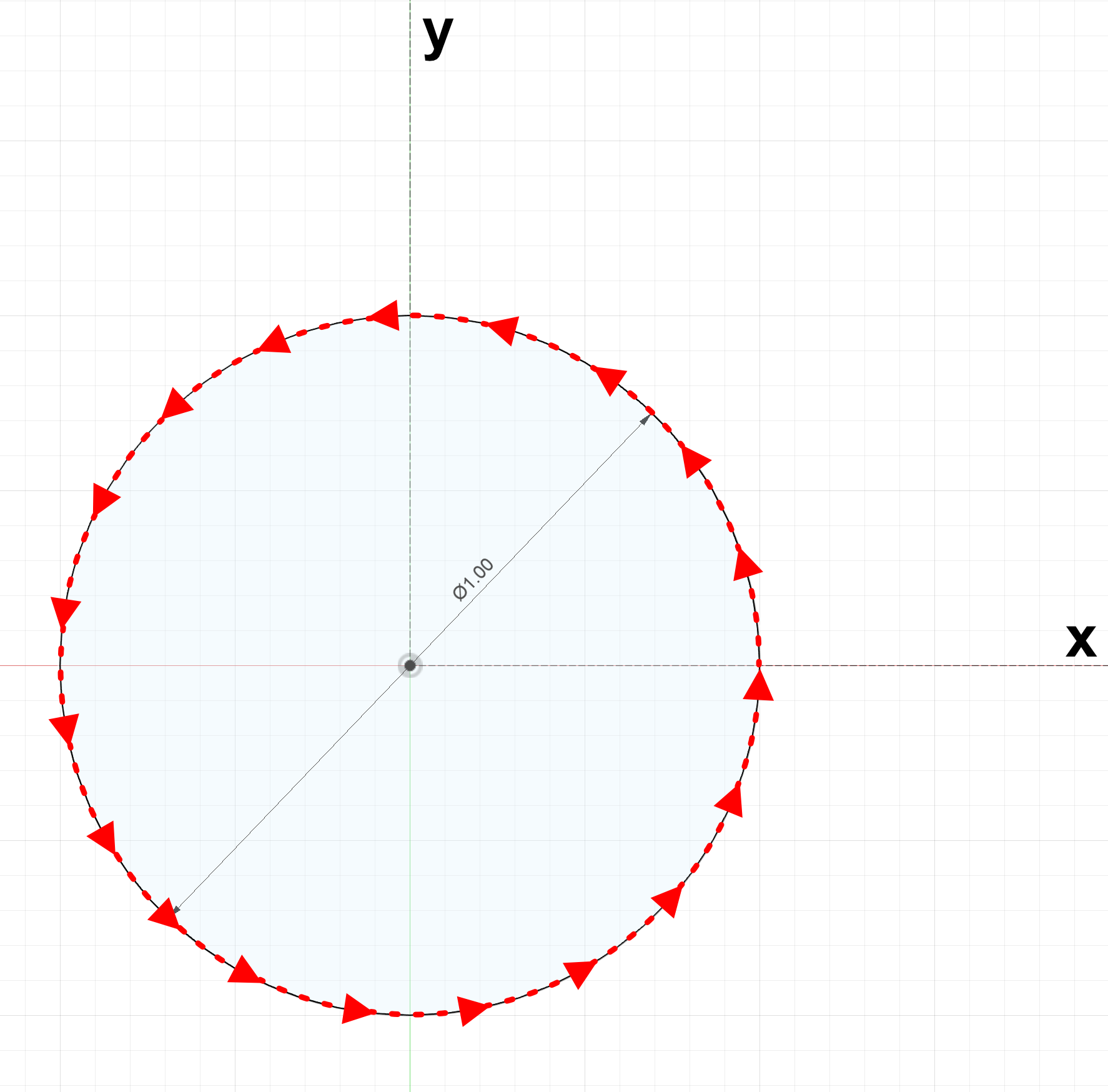
Suppose we wrap a string around the circle, then straighten it out and measure.
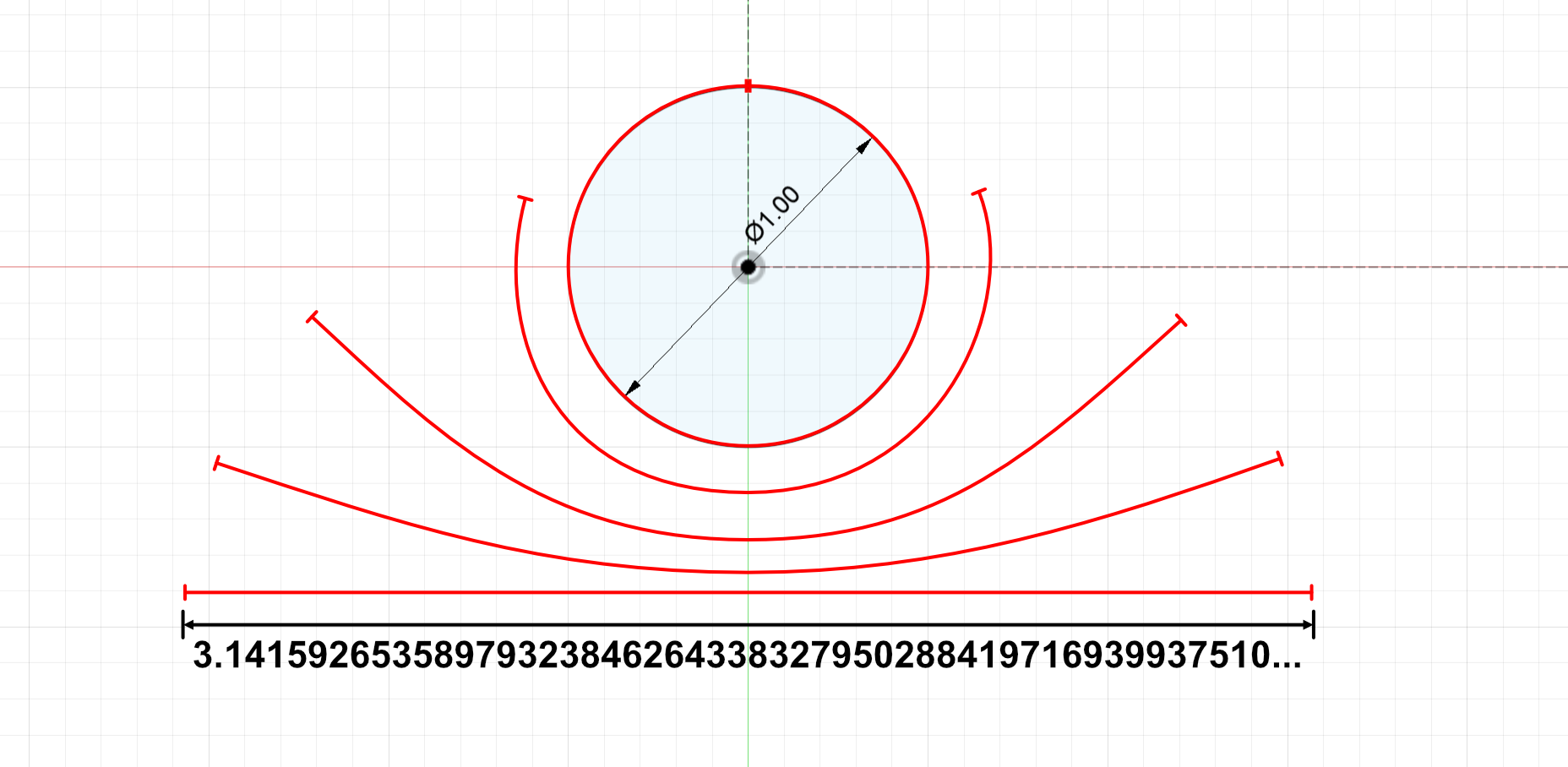
If we had a perfect circle and an extremely precise ruler, we would obtain
$\pi = 3.14159265358979323846 264338327950288419716939937510...$
Note that $\pi$ has an infinite number of digits.
While this string unwrap method provides a good intuition for a direct measurement of $\pi$, there are a lot of practical limitations (accuracy of circle, ruler precision, etc.) There are many practical methods of calculating $\pi$, but because we want to focus on the definition of $\pi$ itself rather than deriving its value, they will be reserved for another article.
When using $\pi$, we often round it to two significant digits:
$\pi = 3.14$
When possible, we generally avoid substituting in a value for $\pi$ and maintain it as a symbolic value until the very end of a calculation when we actually need to obtain a final answer.
Most modern calculators include definitions of $\pi$ with many digits of precision.
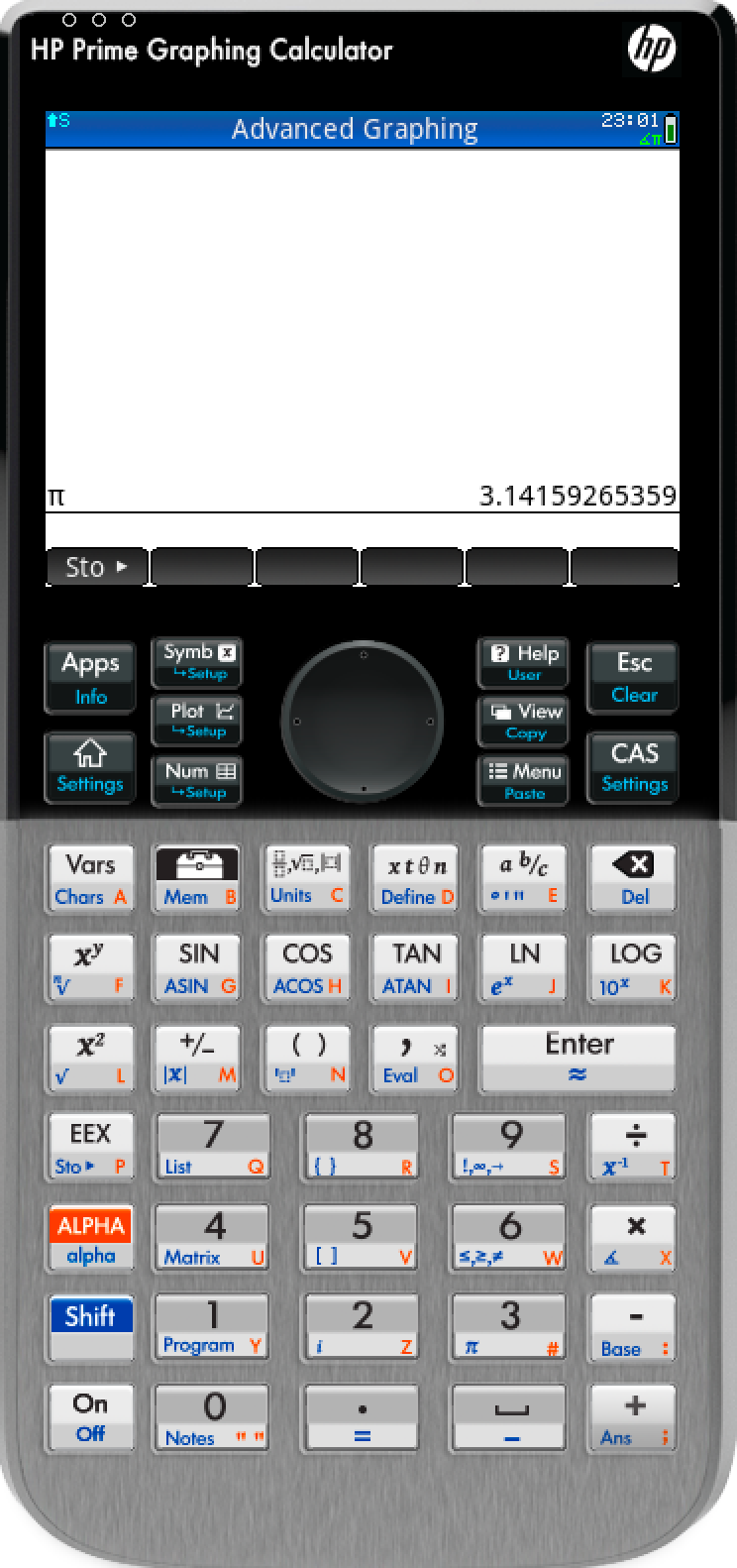
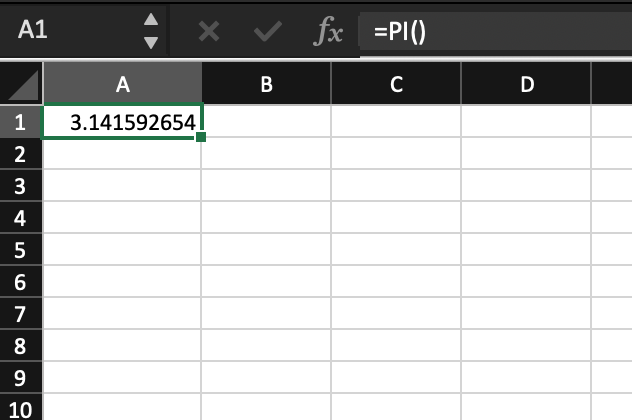
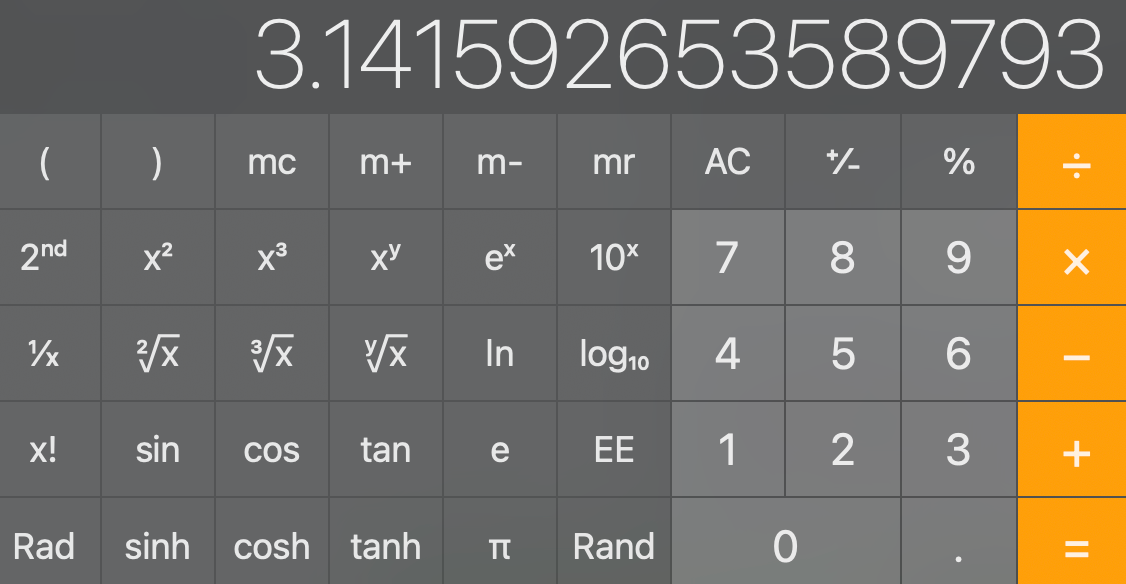
Figure 4: Examples of calculators with built in values for $\pi$ | Left- HP Prime | Center- Microsoft Excel | Right- macOS Calculator
