Symmetry

Symmetry is probably the most powerful concept in all of physics! If something has symmetry, when we look at it from another perspective (or transform it), it doesn't appear any different. This property is also called invariance.

We will see later that this property is deceptively powerful, but in this article, we are seeking only to understand the fundamentals. We will use later use symmetry to motivate every physical model we develop.

Geometric Symmetry

The simplest example of symmetry is geometric symmetry, where shapes are transformed and inspected to check which symmetries exist. In this section, we will consider only 2D shapes.

Translation

To demonstrate translation symmetry of a shape, we simply move the shape around and verify that it doesn't look any different.

Turns out, all geometric shapes have complete translation symmetry. No matter how much translation occurs, they stay the same shape. Note that if we move the camera instead of the shape, the shape still looks the same. This probably seems unremarkable... except that this property gives us a fundamental law so to speak:

A two dimensional shape appears the same to any translated observer.

We call this principle the law of conservation of shape, because the shape is conserved even when viewed by different translated observers.

Rotation

To demonstrate rotation symmetry of a shape, we rotate it. Some shapes, like a square, have only a few select rotations that demonstrate rotation symmetry. A square must be rotated a multiple of 90 degrees (90, 180, 270, 360, etc.)

A circle is unique because it has complete rotation symmetry. Whether the circle is rotated or the camera being used to view it is rotated, the circle remains the same, no matter how much rotation occurs.

Similar to translation, this provides a conservation law for rotated circles:

A circle appears the same to any rotated observer.

For a circle, we can merge the conservation laws for translation and rotation:

A circle appears the same to any rotated and translated observer.

Reflection

To demonstrate reflection symmetry of a shape, we 'reflect' the shape about an axis running through a shape's center point (technically called the centroid).

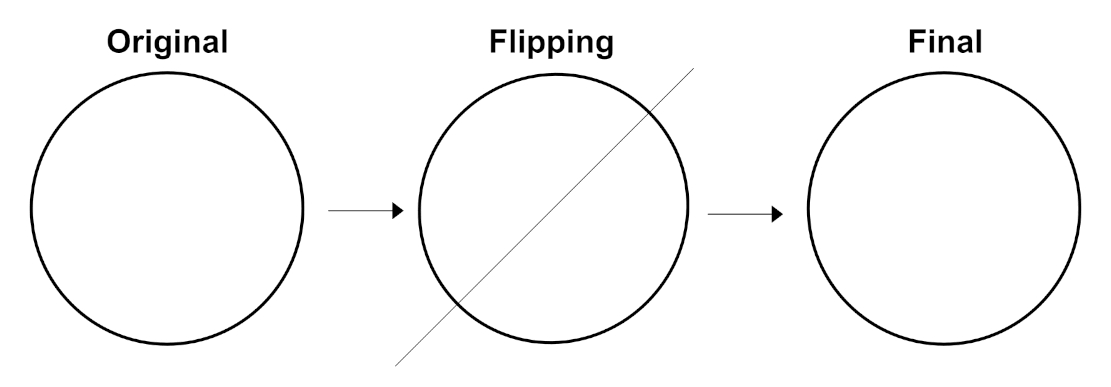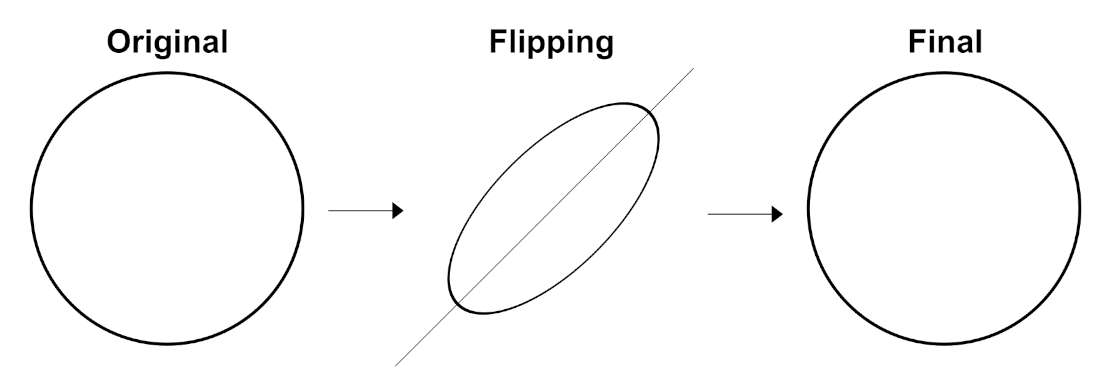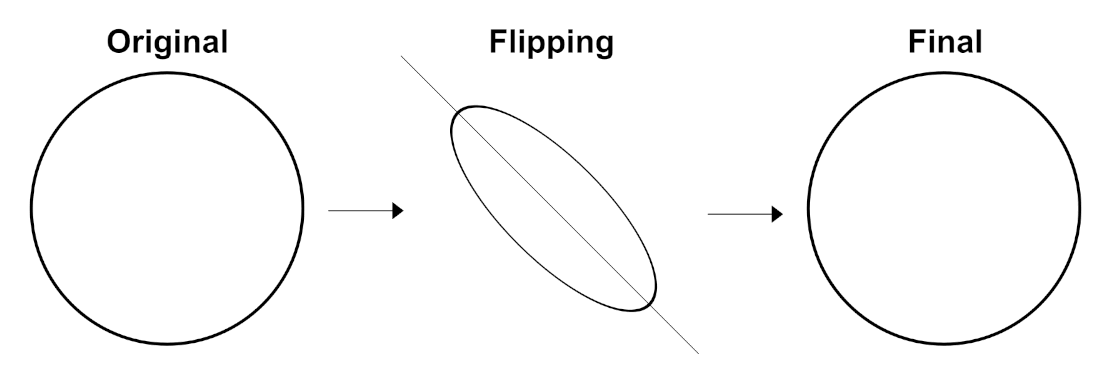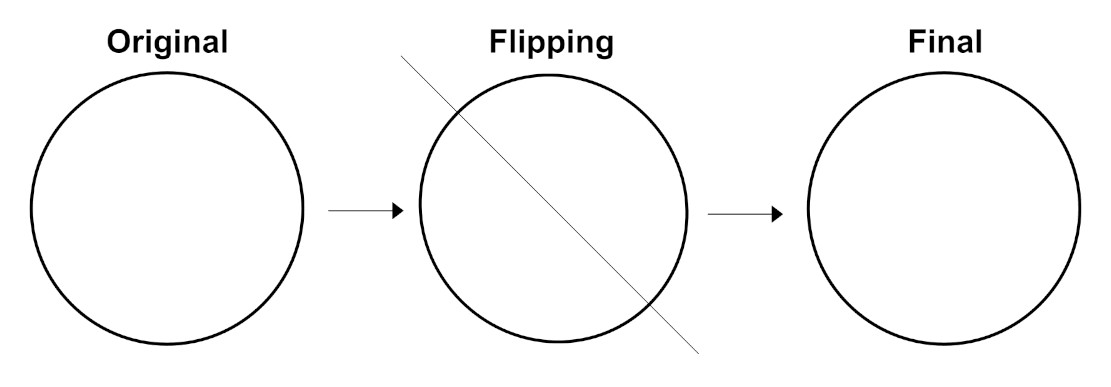
A circle is once again special because it has complete mirror symmetry. No matter which axis is used (as long as the axis intersects the circle's center), the circle appears identical.

How is this useful?

Suppose that you are presented with a shape and asked to prove whether or not it is a circle. Obviously, it would be easy if you were presented with something like a square, but what if you were shown a shape that does appear to be a circle?

Since a circle is uniquely completely rotationally symmetric, if we create a copy of this shape, overlay it, and find a rotational angle where they don't overlap, we've proven that this shape is not a circle. This is demonstrated below, where one copy of the shape is rotated 90 degrees from the other.

With this evidence, we conclude that the shape originally presented is clearly NOT a circle.

There are a lot of ways we could have got about proving that the provided shape wasn't a circle... but exploiting properties of symmetry made the task SO much easier!

Symmetry in Physics

Physics is the science of studying the universe and the processes that take place within it. We previously considered shapes, where the observer might translate or rotate to see what kinds of symmetries hold. We can apply this same strategy to processes of the universe!

Remember the core tenants of science from the article on model based philosophy, observe, model, predict, test.

Philosophy of Model Based Physics

One of the most frustrating parts of my education was how often I was told what I had previously learned was wrong. “Molecules are the most fundamental particle... now it’s atoms... now it’s protons, neutrons, and electrons... now it’s quarks, leptons, and bosons.” “Light behaves like particles... and also now

mechatronics.studioJonathan Bowen

The objective of the physicist is to create models with the highest number of symmetries such that no matter how you observe a process, the prediction should be accurate. It should not matter where or what angle you observe... if your model is effective, it will still make good predictions.

To put another way, no engineer wants to memorize equations they can use on a train but not on a bus. However, we must be a little careful because very few engineers want to memorize equations they can use in Saturn's rings but are needlessly complicated on Earth. We must constantly balance generality and simplicity.

We will eventually decide that there are certain perspectives an earth bound mechatronics engineer doesn't need to concern themselves with (and the accuracy/simplicity tradeoffs will definitely be worth it).

Symmetry in Observations

As an observer, if you undergo a transformation, and any properties of the process you are viewing change, those properties are not symmetric with respect to the transformation. On the flip side, properties that remain constant no matter how a process is viewed are symmetric... commonly called invariant.

Consider a process involving a moving circle.

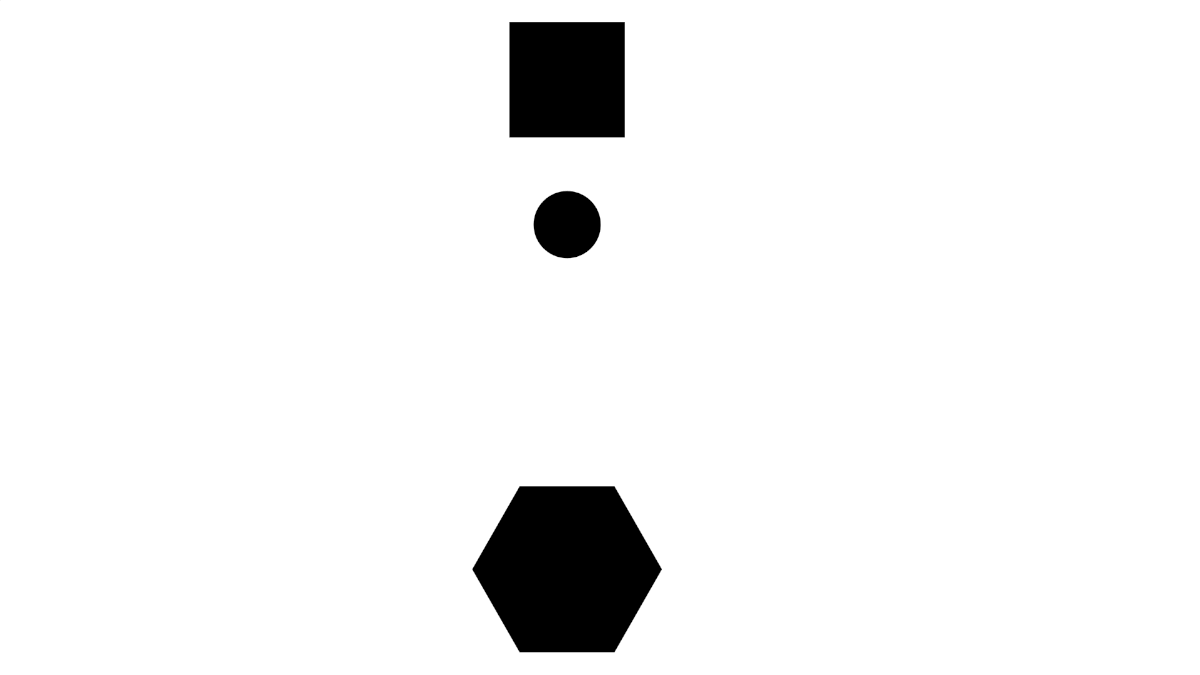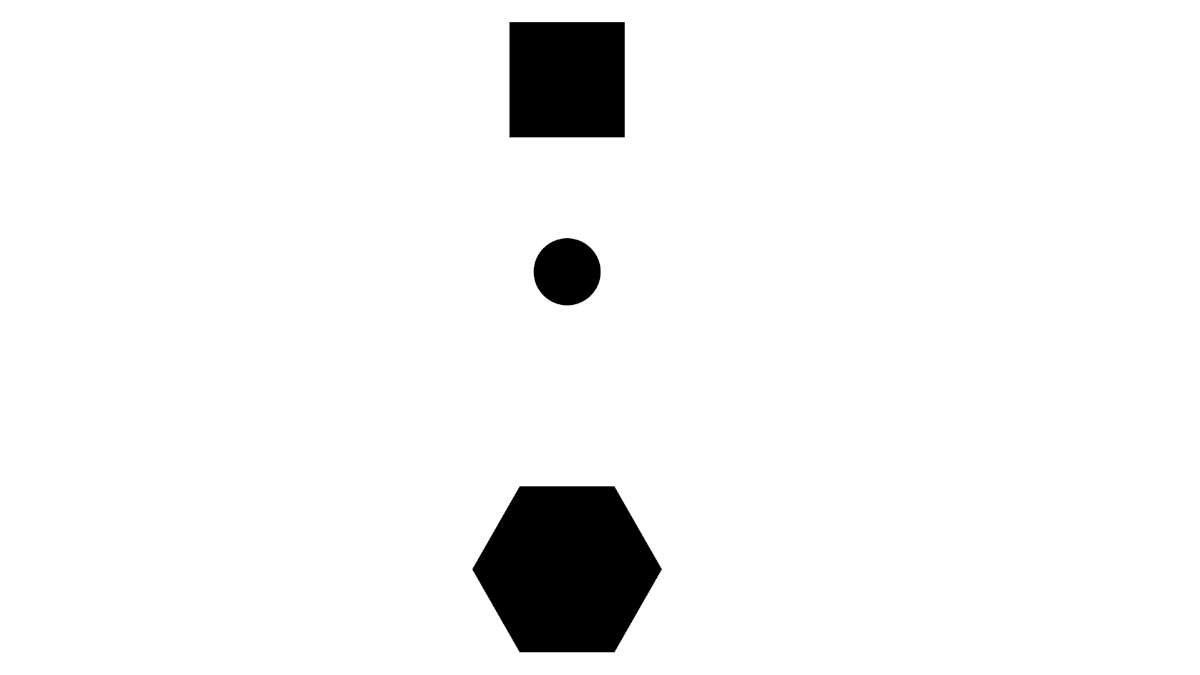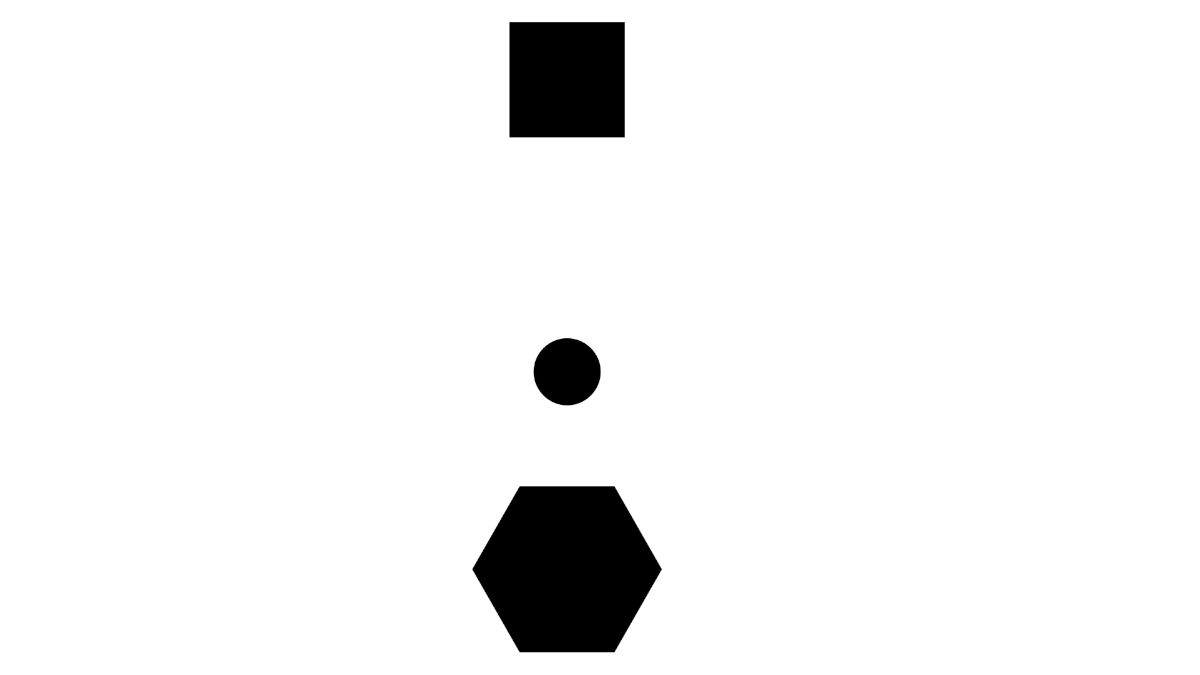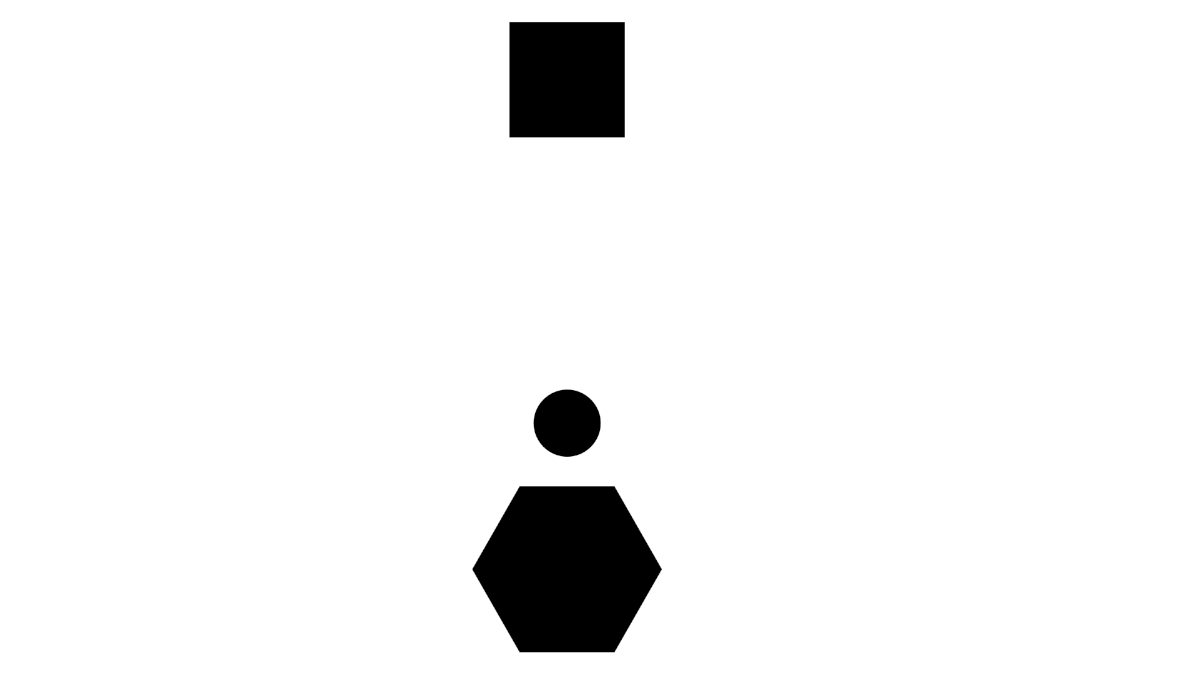
When observing processes, it is very easy to describe them with respect to yourself. You have a natural sense of direction, so you might describe the circle as "falling down", but when you rotate yourself, you now describe the circle as "rising up".

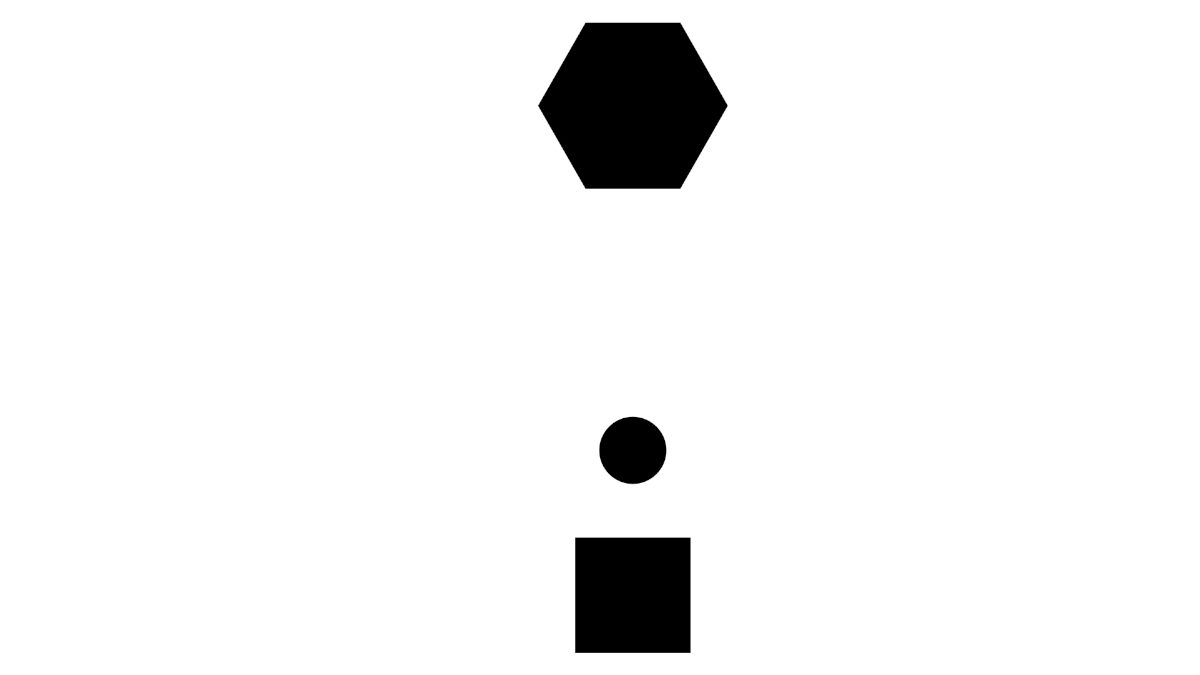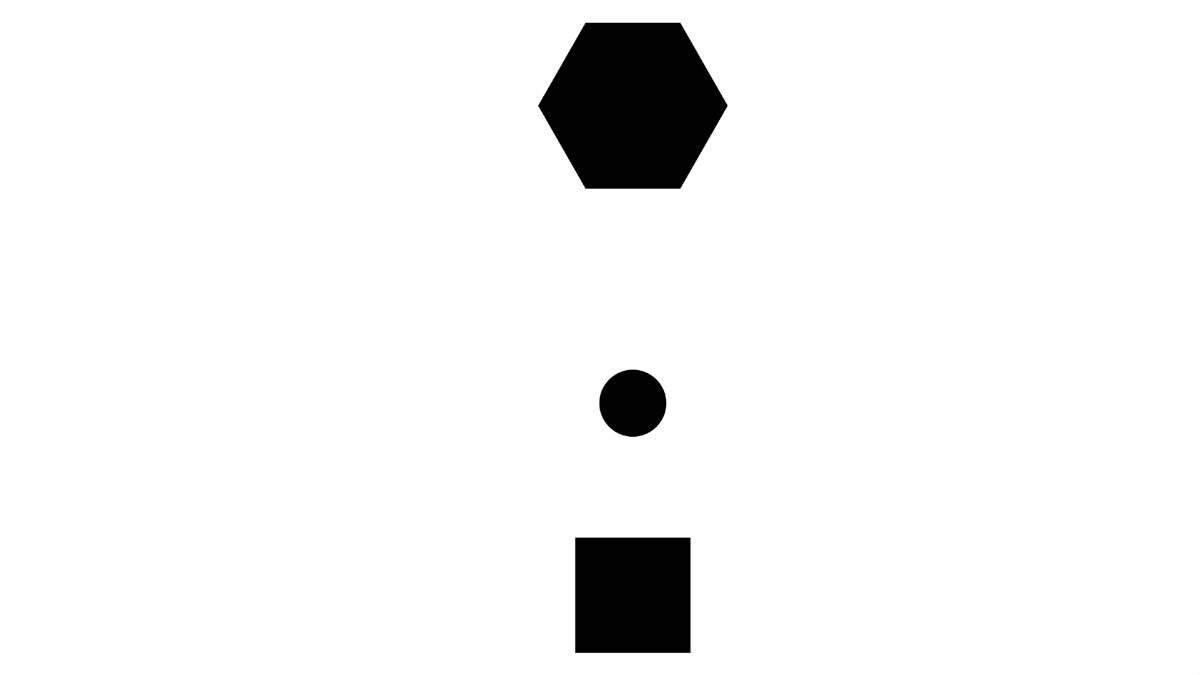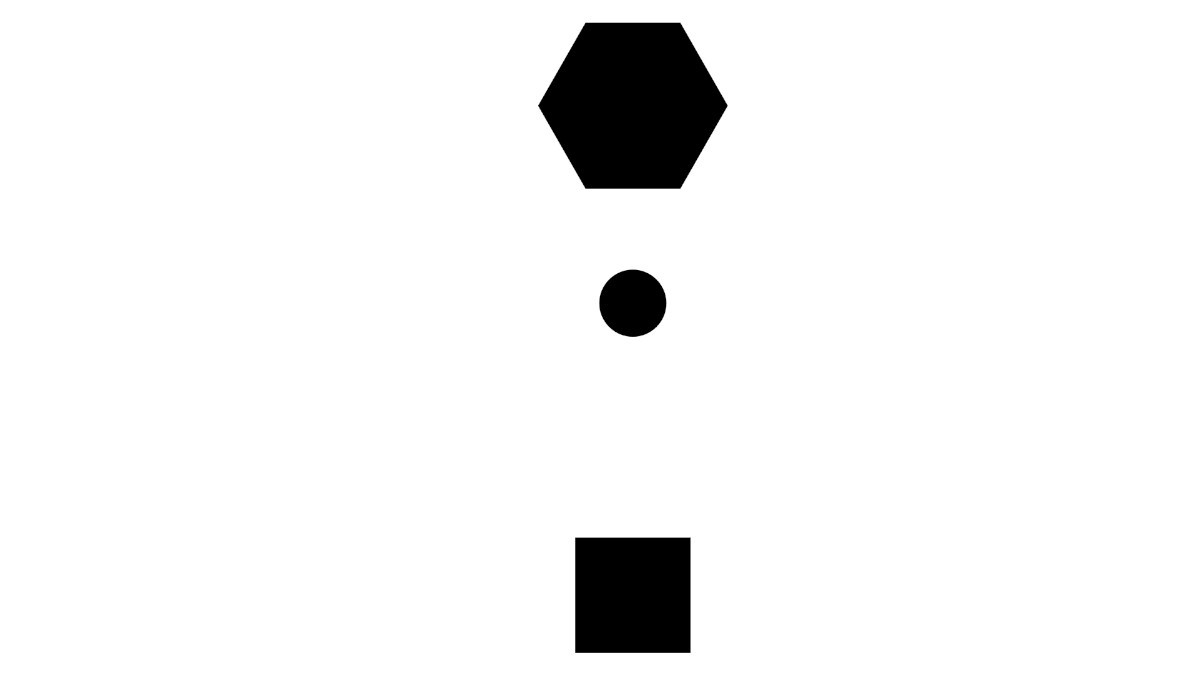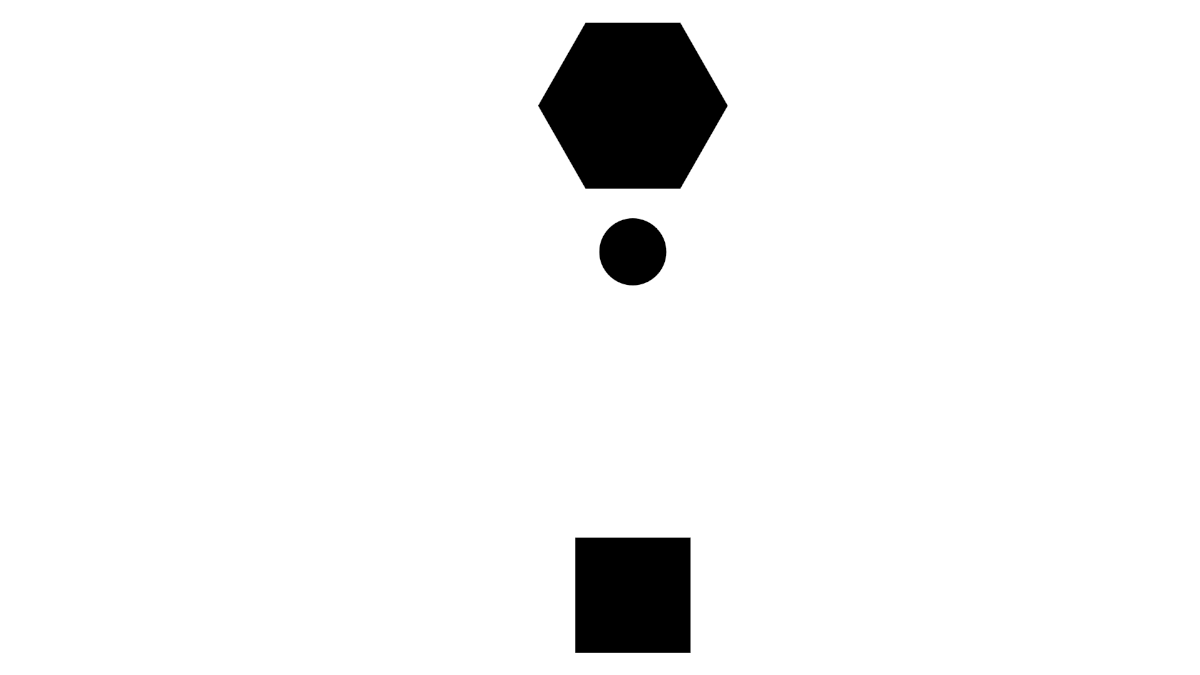
Because your description changes between these two orientations, the model is not symmetric. A more appropriate description might be "the circle moves toward the hexagon". With this description, it does not matter from where or what orientation the observer is watching, the model is valid. Because the description/model is valid from more points of view, it is a better model.

For now, this is all we need on the subject of symmetry, but we will regularly invoke the principle throughout our discussions on physics.